Mathématiques,
concours TSEEAC technicien supérieur de l'aviation civile 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Partie I.
Question 1.
A. Une écriture exponentielle du nombre complexe 2i est 2 exp(i 5p/2 ) ; vrai.
5p/2 = 2p + p/2.
B. Une écriture exponentielle du nombre complexe -5 est -5 exp(-i p ).
exp(- i p ) = -1 ; -5 exp( - i p ) = 5 différent de -5.
C. Une écriture exponentielle du nombre complexe 2i est -2 exp(-ip/2 ) ; vrai.
exp(-ip/2 ) = -i ; -2 exp(-ip/2 ) = -2 *(-i) = 2i.
D. Une écriture exponentielle du nombre complexe -5 est -5 exp(i p ).
exp( i p ) = -1 ; -5 exp( i p ) = 5 différent de -5.
Question 2.
A. Une écriture exponentielle du nombre complexe 0 est 0 exp(-i q ), q étant un nombre réel. Vrai.
B. 0 n'a pas d'écriture exponentielle.
Le nombre zéro a une partie réelle qui vaut zéro et une partie complexe nulle. Son argument est nul.
C. Une écriture exponentielle du nombre complexe cos (p / 5) -i sin (p /5) est : exp(ip / 5).
cos (p / 5) -i sin (p /5) = cos (-p / 5) +i sin (-p /5) = exp( - ip / 5).
D. Une écriture exponentielle du nombre complexe cos (p / 5) -i sin (p /5) est : exp(- ip / 5). Vrai.
Question 3.
Une écriture exponentielle du nombre complexe 2sin (p / 7) +2 i cos (p /7) est :
A. 2 exp( i 9p / 14). B. 2 exp( i 5p / 14) vrai. C. 2 exp( i 6p / 7). D. 2 exp( i 8p / 7).
sin (p / 7) = cos ( p / 2-p / 7) =cos ( 5p / 14).
cos (p /7) = sin ( p / 2-p / 7) =sin ( 5p / 14).
2sin (p / 7) +2 i cos (p /7) = 2(cos ( 5p / 14) + i sin ( 5p / 14))=2 exp( i 5p / 14).
Question 4.
Une écriture exponentielle du nombre complexe z' = (-2*3½ +2i) / (1+i)4 est :
A. exp(- i p / 6) vrai. B. exp( i 7 p / 12). C. 2 exp(- i p / 6). D. 0,5 exp( i 7 p / 12).
z =(-2*3½ +2i) ; |z|=((-2*3½)2 +22)½ =4.
z / |z|= (- 3½/ 2 +0,5i) = cos (5p /6)+i sin ( 5 p / 6) ; z = 4 exp(5 p / 6).
|1+i |=(12 +12)½ = 2½ ; (1+i) /|1+i|= cos( p / 4)+ i sin( p / 4) ; 1+i =2½exp(i p / 4) ; (1+i)4 = 4 exp(i p).
z' = 4 exp(5 p / 6) / (4 exp(i p)) = exp( i (5 p / 6 -p)=exp( - i p / 6).
Question 5.
Une écriture exponentielle du nombre complexe z' = i(1 +i)3 / (3½-i)5 est :
A. 2½ / 32 exp( ip /12).
B. 2½ / 32 exp(i 5p /12).
C. 2½ / 16 exp(ip /12). Vrai.
D. 2½ / 16 exp(i 5p /12).
i = exp(i p /2) ;
(1 +i)=2½exp(i p / 4) ; (1+i)3 =2* 2½ exp(i 3 p / 4).
|3½-i| =(3+1)½ = 2. (3½-i) / |3½-i| = 3½ / 2 -i / 2 =cos (-p /6 ) + i sin(-p /6)
3½-i =2 exp(-i p /6) ; (3½-i)5 = 25 exp(-i 5 p /6).
z' = 2* 2½ / 25 exp(i 3 p / 4) exp(i p /2) / exp(-i 5 p /6).
z' = 2½ / 16 exp (i (3 p / 4 +p /2 +5 p /6)) = 2½ / 16 exp (i 25 p / 12) ;
25 p / 12 = 2 p + p / 12 ; z' = 2½ / 16 exp (i p / 12) ;
Question 6.
On note z1 = 1 +i et z2 = 1-i 3½. La forme algébrique de z1 x z2 est :
A. 1-3 ½ +i(1-3 ½). B. 1+3½ +i(1+3½). C. 1-3½ +i(1+3½). D. 1+3½ +i(1-3½). Vrai.
z1 x z2 =(1+i)(1-i 3½)=1 -i2 3½ +i(1-3½)=1 + 3½ +i(1-3½).
Question 7.
Une écriture exponentielle de z1 x z2 est :
A. 2 exp( -i p /12).
B. 2 exp(i 5p /12).
C. 2½ /2 exp(i 7p /12). Vrai.
D. 2½ / 2 exp( -i p /12).
z1 = 1 +i = 2½exp(i p/4).
| z2 |=(1+3)½ = 2 ; z2 / | z2 |=0,5 - i 3½ / 2 ; z2 = 2 ( cos (-p/3) + i sin (-p/3) = 2 exp(-i p / 3).
z1 x z2 = 2 *2½ exp(i ( p /4-p /3) =2 *2½ exp( - i p /12).
E. aucune des réponses proposées.
Question 8.
On en déduit que :
A. cos (7p/12) = (1+3½) / 2 et sin (7p/12) = (3½-1) / (2*2½).
B. cos (7p/12) = (1-3½) / (2*2½) et sin (7p/12) = (3½-1) / 2.
C. cos (p/12) = (1+3½) / (2*2½) et sin (p/12) = (3½-1) / (2*2½). Vrai.
D. cos (p/12) = (1-3½) / 2 et sin (p/12) = (3½-1) / 2
2 *2½ exp( - i p /12) = 1 + 3½ +i(1-3½) .
2 *2½ [cos( - p /12) +i sin( - p /12) =1 + 3½ +i(1-3½).
2 *2½ [cos( p /12) -i sin( p /12) =1 + 3½ +i(1-3½).
Partie II.
Question 9.
L'équation différentielle y'-2y =0, notée (E) admet pour ensemble de solutions :
A. f(x) = k e2x avec k réel. Vrai.
B. f(x) = e2x.
C. f(x) = k e-2x avec k réel.
D. f(x) = k e0,5x avec k réel.
Question 10.
La solution f de (E) dont la courbe représentative C dans un repère donné passe par le point A(1 ; 2) est :
A. f(x) = 2 e2x-2 . Vrai.
B. f(x) = -2e2x+2.
C. f(x) = 2 e2x+2 .
D. f(x) =-2 e3-2x .
2= k e2 ; k = 2 /e2 = 2 e-2 ; f(x) = 2e-2 e2x = 2 e2x-2 .
Question 11.
La solution f de (E) dont la courbe représentative C dans un repère donné passe par le point A(1 ; -2) est :
A. Strictement croissante sur R.
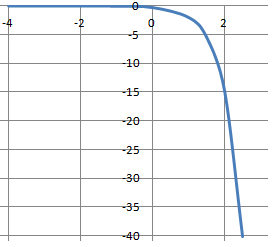
B. Strictement décroissante sur R. Vrai.
C. La courbe C admet l'axe des abscisse comme asymptote en -oo. Vrai.
D. La courbe C admet l'axe des abscisse comme asymptote en +oo.
-2= k e2 ; k = -2 /e2 = 2 e-2 ; f(x) = -2e-2 e2x = -2 e2x-2 .
f '(x) = -4e2x-2 < 0 ; f(x) strictement décroissante sur R.
f(x) tend vers zéro quand x tend vers -oo.
Question 12.
La
solution g de l'équation dofférentielle y'=2y+4, notée (E') dont la
courbe représentative C possède une tangente parallèle à la droite
d'équation y = x en son point d'abscisse 1 est :
A. g(x) = 0,5 e2x-2 -4.
B. g(x) = 0,5 e2x+2 -2.
C. g(x) = 0,5 e2x+2 -4.
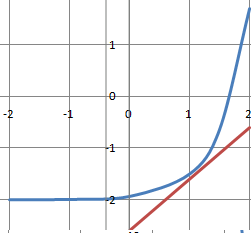
D. g(x) = 0,5 e2x-2 -2. Vrai.
Solution générale de y'-2y =0 : f(x) = k e2x.
Solution particulière de (E') : f(x) = -2.
Solution générale de (E') : g(x) = k e2x-2 avec k réel.
g'(x) =2ke2x ; g'(1) = 2ke2.
Coeficient directeur de la tangente en x = 1 : 1 =2ke2 ; k = 0,5 e-2.
g'x) = 0,5 e2x-2 -2.
Question 13.
Les deux nombres réels a et b tels que la fonction f(x) = ax+b +ln(x) soit une solution particulière de l'équation différentielle
y' = 2y +4x+6+1 / x -2 ln(x), notée (E") sont :
A. a = 2 et b = -4 ; B. a = 2 et b = -1 ; C. a = -2 et b = 4 ; D. a = -2 et b = -4. Vrai.
f '(x) =a+1 / x.
Repport dans (E") : a + 1 / x = 2ax+2b+2ln(x)+4x+6+1 / x -2 ln(x).
a =(2a+4)x +2b+6.
On identifie : a =2b+6 et 2a+4=0 soit a = -2 ; b = -4.
Question 14.
On admet qu'une fonction h est solution de (E") si et seulement si la fonction h-f est solution de (E). On en déduit que l'ensemble des solutions de (E") est :
A. h(x) = -2x+4+ln(x)+ke2x avec k réel.
B. h(x) = -2x-4+ln(x)+ke-2x avec k réel.
C. h(x) = -2x-4+ln(x)+ke2x avec k réel. Vrai.
D. h(x) = -2x+4+ln(x)+ke-2x avec k réel.
h-f est solution de (E) : h-f =ke2x.
h(x) = ke2x+f =ke2x-2x-4 +ln(x)
Question 15.
La solution F de (E") dont la courbe représentative passe par le point A(1 ; -2) est :
A. F(x) = -2x-4+ln(x)+4e2x-2 .Vrai
B. F(x) = -2x+4+ln(x)+4e2x-2 .
C. F(x) = -2x-4+ln(x)+4e2x+2 .
D. F(x) = -2x+4+ln(x)+4e2x+2 .
-2=ke2-2-4 ; k = 4e-2.
|
...
|
....
|
Partie III.
Question 16.
Pour n entier naturel, la suite définie par un = 2n2-13n+1 :
A. est strictement croissante.
B. est strictement décroissante.
C. Pour n > 2, est strictement croissante.
D. Pour n > 2, est strictement décroissante.
un+1 -un = 2(n+1)2-13(n+1)+1- 2n2+13n-1=2(n2+1+2n)-13n-13+1 - 2n2+13n-1=4n-11.
un+1 -un > 0 si n > 3.
Pour n > 3, la suite est strictement croissante.
E. Aucune des réponses proposées.
Question 17.
Pour n entier naturel, la suite définie par le terme général vn = (2n+1)en :
A. est strictement croissante. Vrai.
B. est strictement décroissante.
C. Pour n > 2, est strictement croissante.
D. Pour n > 2, est strictement décroissante.
vn+1-vn =(2(n+1)+1)en+1- (2n+1)en= en [2(n+1)+1)e-2n-1]=en [(2n+3)e-2n-1]=en [2n(e-1)+3e-1]
en > 0 ; on étudie le signe de 2n(e-1)+3e-1.
2n(e-1)+3e-1 > 0 ; n >(1-3e) / (2(e-1).
Or n > 0 et (1-3e) / (2(e-1) < 0, donc n >(1-3e) / (2(e-1) est vraie.
Question 18.
Pour n entier naturel, la suite définie par wn = n-ln(1+n2) :
A. n'est pas strictement monotone. Vrai.
B. n'est pas monotone. Vrai.
C. est strictement croissante.
D. est strictement décroissante.
wn+1-wn =n+1-ln(1+(n+1)2) -n+ln(1+n2)=1-ln(1+(n+1)2)+ln(1+n2) = 1 +ln[(1+n2) / (1+(n+1)2)].
Etude du signe de 1 +ln[(1+n2) / (1+(n+1)2)].
1 +ln[(1+n2) / (1+(n+1)2)] > 0 ; ln[(1+n2) / (1+(n+1)2)] > -1.
(1+n2) / (1+(n+1)2)] > e-1 =1/e ; e((1+n2) >1+(n+1)2 ;
e(1+n2) >2+n2+2n ; n2(e-1)-2n +e-2 >0.
Discriminant D =4-4(e-2)(e-1)>0, donc deux racines réelles.
Question 19.
Pour n entier naturel, la suite définie par xn = (-1)nln(n ) :
A. n'est pas strictement monotone. Vrai.
B. n'est pas monotone. Vrai.
C. est strictement croissante.
D. est strictement décroissante.
xn+1-xn =(-1)n+1ln(n+1 )- (-1)nln(n )= -1 * (-1)nln(n+1 )- (-1)nln(n )= -[ (-1)n (ln(n+1) +ln(n)] = -(-1)nln(n(n+1)).
xn+1-xn < 0 si n est pair et xn+1-xn > 0 si n est impair.
Question 20.
Pour n entier naturel, la suite définie par yn+1 = exp (yn-2) et y0 = 2. :
A. n'est pas strictement monotone.
B. n'est pas monotone.
C. est strictement croissante.
D. est strictement décroissante. Vrai.
y1 = exp (y0-2) = 1.
Démonstrons par récurrence que yn+1 < yn :
Initialisation : y1 -y0 < 0 est vraie.
Hérédité : yn+1 < yn est supposée vraie.
yn+2 = exp (yn+1-2) ; yn+2 -yn+1=exp (yn+1-2) -exp (yn-2) =exp(yn+1) e-2 -exp (yn) e-2 =e-2 (exp(yn+1) -exp (yn)).
yn+1 < yn donc exp(yn+1) < exp (yn).
De plus e-2 >0 , donc yn+2 < yn+1.
Conclusion : la propriété est vraie au rang 0 et héréditaire, elle est vraie pour tout n entier naturel.
Question 21.
Soit la fonction f(x) = x +sin(2px) et n un entier naturel.
A. La suite définie par un = f(n) est décroissante.
B. La suite définie par un = f(n) est croissante. Vrai.
C. La fonction f est décroissante.
D. La fonction f est croissante.
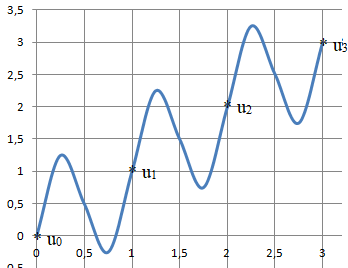
La fonction f n'est ni croissante, ni décroissante sur R.
un+1-un = f(n+1)-f(n) =n+1+sin(2p(n+1))- n -sin(2p n) =1-sin(2p(n+1))-sin(2p n).
n est un entier, donc sin(2p n) =sin(2p(n+1))=0.
un+1-un =1 soit un+1>un.
Partie IV.
Question 22.
Soit f une fonction réelle à variable réelle définie par :
f(x) = ax+0,2 si x appartient à [0 ; 4] et f(x) = 0 si x n'appartient pas à [0 ; 4].
Pour que f définisse une loi à densité sur l'intervalle [0 ; 4], il faut et il suffit que le nombre a soit égal à :
A. 0,1 ; B. 1 /40 vrai ; C. 0,8 ; D. 1.
Primitive de f(x) : F(x) = 0,5 ax2 +0,2 x + Cste.
F(4) -F(0) = 8a+0,8= 1 ; 8a = 0,2 ; a = 0,2 / 8 =1 / 40.
Question 23.
On note X la variable aléatoire définie sur [0 ; 4] dont la loi de probabilité a pour densité la fonction f précédente.
A. P(X < 1 ) =19 / 80.
B. P(X < 1 ) =1/4.
C. P(X < 1 ) =3 / 5.
D. P(X < 1 ) =7 / 10.
F(1) -F(0) =[x2 / 80+0,2x]01 =1 /80 +0,2 =1 /80 +16 /80 =17 /80.
E. Aucune des réponses proposées.
Question 24.
A. P(X > 2 ) =5 / 32.
B. P(X > 2 ) =1/5.
C. P(X > 2 ) =11 / 20. Vrai.
D. P(X > 2 ) =5 / 26.
P(X > 2 ) = 1-P(X < 2 )=1-(F(2) -F(0)) =1-[x2 / 80+0,2x]02 =1-(4 /80 +0,4 )=1-1 /20 -2 / 5 =11 / 20.
Question 25.
A. P(0,5 <X > 3 ) =41 / 80.
B. P(0,5 <X > 3 ) =43 / 80.
C. P(0,5 <X > 3 )=38 / 64.
D. P(0,5 <X > 3 ) =39 / 64. Vrai.
F(3) -F(0,5) =[x2 / 80+0,2x]0,53 =9 / 80 +0,6 - (1/ 320 +0,1) =(36 +192 -1 - 32)/ 320 =195 / 320 =.39 / 64.
|
|
|
|