Math�matiques,
concours TSEEAC technicien sup�rieur de l'aviation civile 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
.
.
|
..
..
......
...
|
Question 1.
Soit n un entier naturel non nul. On d�finit la fonction fn par fn(x) = 2enx / (enx+5) et la suite (un) par l'expression :
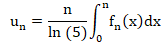
On peut montrer que :
A. La suite (un) est strictement croissante. Vrai.
B. La suite (un) est strictement d�croissante.
C. La suite (un) est convergente.
D. La suite (un) est constante.
On pose u = enx+5 ; u' = nenx.
Primitive de fn(x) : Fn(x) = 2 / n ln((enx+5).
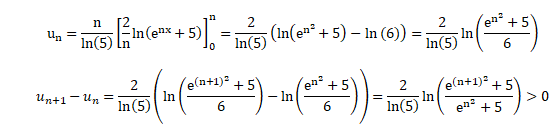
Quand n tend vers +oo, un tend vers +oo ; la suite (un) diverge.
Question 2.
On d�finit sur R la fonction f par :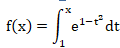 
A. f(x) est strictement d�croissante.
B. f(x) est strictement croissante. Vrai.
C. f n'admet pas de maximum.
D. On ne peut rien dire au sujet de la monotonie de f.
La d�riv�e de f(x) est la fonction exp(1-t2) > 0 ; f(x) est strictement croissante.
Question 3.
La
lettre n d�signant un entier naturel non nul, on consid�re une urne qui
contient n boules blanches et 3 boules noires, indiscernables au
toucher. On tire successivement et sans remise deux boules dans cette
urne.
A.
Il existe deux entiers naturels n pour lesquelles la probabilit�
d'obtenir deux boules de couleurs diff�rentes est �gale � 9 / 22.
B. Il
existe un entier naturel n pour lesquelles la probabilit� d'obtenir
deux boules de couleurs diff�rentes est �gale � 9 / 22. Vrai.
C. Il
n'existe pas d' entier naturel n pour lesquelles la probabilit� d'obtenir
deux boules de couleurs diff�rentes est �gale � 9 / 22.
D. La probabilit� d'obtenir deux boules de couleurs diff�rentes est : 6 n /((n+3)(n+1)).
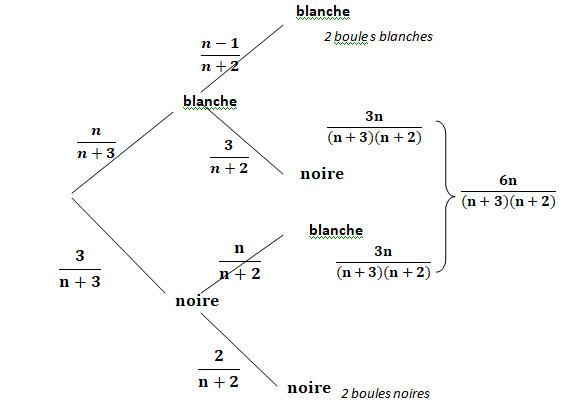
6 x 22 n = 9(n+3)(n+2) ; 44 n =3(n+3)(n+2) =3n2+15n +18.
3n2-29n +18=0.
Discriminant D =292-4*3*18=625=252.
On retient la racine enti�re positive :
n1 =(29-25) / 6 =2 /3 ; n2 =(29+25) / 6 =9.
Question 4.
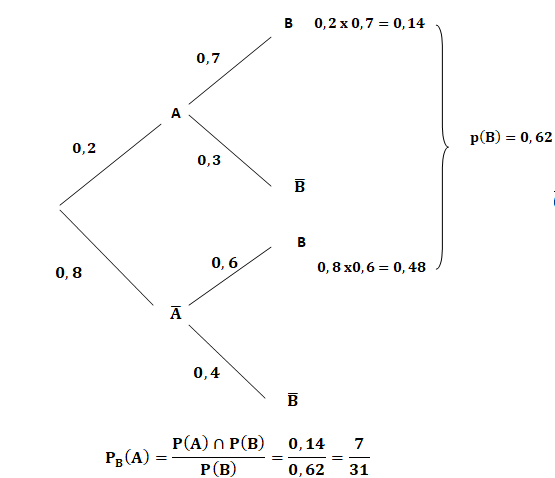
On
consid�re l'arbre de probabilit� ci-dessous. La probabilit� que
l'�v�nement A soit r�alis� sachant que l'�v�nement B est r�alis� est :
A. 7 /31 vrai. B. 6 / 31. C. 7 / 30. D. 6 / 30.
Question 5.
On consid�re l'algorithme ci-dessous. Lorsqu'on saisit la valeur n = 6, la valeur u affich�e est :
A. 2,44. B. 2,27.C. 2,4. D. 2,23.
i et n sont des entiers naturels et u est un r�el.
Demander � l'utilisateur la valeur n.
Affecter � u la valeur 0.
Pour i allant de 1 � n
Affecter � u la valeur u+1 / i.
Afficher u.
i
|
1
|
2
|
3
|
4
|
5
|
6
|
u
|
0+1=1
|
1+0,5=1,5=3 /2
|
3/2+1/3=11 / 6
|
11/6+1/4=25/12
|
25/12+1/5=137/60
|
137/60+1/6=147/60 ~2,45
|
Question 6.
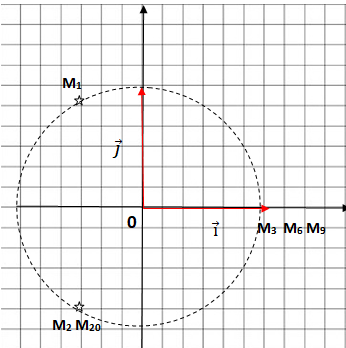
Dans le plan complexe muni d'un rep�re orthonorm�, pour tout entier naturel n non nul, on consid�re les points Mn d'affixe
zn = exp(2 np i /3).
A. Les points O, M 1 et M 20 sont align�s.
B. Les points O, M6 et M9 sont align�s. Vrai.
C. Le triangle OM1M20 s'il existe est �quilat�ral.
D. Le triangle OM6M9 s'il existe est �quilat�ral.
z1 = exp(2 p i /3). z2 = exp(4 p i /3). z3 = exp(6 p i /3) = exp(2 p i).
z6 = exp(12 p i /3)=exp(2 p i).
z9 = exp(18 p i /3)=exp(2 p i).
z20 = exp(40 p i /3)=exp(4 p i /3)..
Question 7.
Soit (un) une suite non constante de nombres r�els. Pour tout entier naturel n, on pose vn = sin(un). Vrai.
A. On peut choisir une suite (un) afin que la suite (vn) converge vers 2� /2.
Si un = 45-1/10n alors(vn) converge vers 2� /2.
B. On peut choisir une suite (un) afin que la suite (vn) converge vers 1. Vrai.
Si un = 90-1/10n alors(vn) converge vers 1.
C. La suite (vn) converge toujours.
D. La suite (vn) diverge toujours.
Question 8.
L'espace est rapport� � un rep�re orthonorm�. La repr�sentation param�trique de la droite (d) est :
x =t+3 ; y = -t+5 ; z=2.
La sph�re (S) est centr�e en A(1 ; -1 ; 0) et son rayon vaut R=6.
A. La droite (d) et la sph�re (S) sont s�cantes.
B. La droite (d) et la sph�re (S) sont s�cantes en deux points.
C. La droite (d) et la sph�re (S) ne sont pas s�cantes.
D. La droite (d) et la sph�re (S) sont tangentes. Vrai.
Equation de la sph�re : (x-1)2 +(y+1)2 +z2 = 36.
Les coordonn�es d'un point commum � la droite et � la sph�re v�rifient :
(t+3-1)2 +(-t+5+1)2 +22 = 36.
t2+4+4t+t2+36-12t+4=36.
2t2-8t+8=0 ; t2-4t+4=0 ; (t-2)2 =0 soit t = 2.
|
...
|
....
|
Question 9.
L'espace est rapport� � un rep�re orthonorm�. La repr�sentation param�trique de la droite (d) est :
x =2t+3 ; y = -2t-1 ; z=6t+2.
La repr�sentation param�trique de la droite (d') est :
x =-t-1 ; y = t-1 ; z= -3t.
A. Les deux droites sont confondues.
B. Les deux droites sont s�cantes.
C. Les deux droites sont non s�cantes et coplanaires. Vrai.
D. Les deux droites sont non s�cantes et non coplanaires.
Si les droites sont s�cantes : 2t+3 =-t-1 soit t =4/3.
Repport dans y : -8 /3 -1 = -11 /3 diff�re de 4/3-1.
Les droites ne sont donc pas s�cantes.
Coordonn�es d'un vecteur directeur de (d) : 2 ; -2 ; 6.
Coordonn�es d'un vecteur directeur de (d') : -1 ; 1 ; -3.
Ces deux vecteurs �tant colin�aires, les deux droites sont parall�les.
Deux droites sont coplanaires si et seulement si elle sont s�cantes ou parall�les.
Question 10.
Soit X une variable al�atoire dont la densit� de probabilit� est une fonction f d�finie par :
f(x) = m sin (x) pour x appartenant � [0 ; p] sinon f(x) = 0.
m est un nombre r�el qui sera choisit en cons�quence.
On peut v�rifier que :
A. Pour x appartenant � ] p ; +oo[, P(X < x) = 0,5.
B. P(X > 0) = 0.
C. Pour x appartenant � [0 ; p ], P(X < x) = 0,5 -0,5 cos (x) et pour x appartenant � ]-oo ; 0[, p(X < x)=0. Vrai.
D. P(p/4 < X < 3p/4)=2� /2. Vrai.
Primitive de f(x) : F(x) = -m cos (x) +Cste.
P(0 < X < p)=1 =[-m cos (x) +Cste ]0p =-m cos p +m cos (0) =2 m soit m = 0,5.
P(X < x) =[-0,5 cos (x) +Cste ]0x = -0,5 cos x +0,5 cos (0) =0,5-0,5 cos (x).
P(p/4 < X < 3p/4) =[-0,5 cos (x) +Cste ]p/43p/4 = -0,5 cos 3p/4 +0,5 cos (p/4) = -0,5(-2� /2)+ 0,5*2� /2=2� /2. .
Question 11.
Soient les nombres complexes d�finis par z1 = 2� +i 6� et z2 = 2+2i. Le nombre complexe d�fini par z = z1 / z2 v�rifie :
z=( 2� +i 6�) (2-2i) / [(2+2i)(2-2i)] =( 2 *2�+2*6�) +i(2*6�-2 *2� )] / 8=( 2�+6�) +i(6�-*2� )] / 4.
R�ponse A.
Question 12.
Les nombres complexes z1 et z2 v�rifient :
A. z1 a pour module 2� et pour argument p /3.
B. z1 a pour module 2*2� et pour argument 2p /3.
|z1 |=(2+6)� = 2*2� ; z1 / |z1 |=0,5+ i 3� /2.
z1 = 2*2� exp(i p /3).
C. z2 a pour module 2� et pour argument p /4.
D. z2 a pour module 2*2� et pour argument 3p /4.
|z2 |=(4+4)� = 2*2� ; z2 / |z2 |=2� / 2+ i 2� / 2.
z2 = 2*2� exp(i p /4).
E. Aucune des r�ponses propos�es.
Question 13.
On en d�duit :
A. z a pour module 2 et pour argument 5 p /12.
B. z a pour module 0,5 et pour argument -5 p /12.
C. z a pour module 1 et pour argument p /12. Vrai.
D.z a pour module 1 et pour argument - p /12.
z = exp(i p /3) / exp(i p /4) = exp( i p / 12)
Question 14.
On obtient alors :
A. cos (p/12) = (6�-2�) / 4 et sin (p/12) = (6�+2�) / 4.
B. cos (p/12) = (6�-2�) / 2 et sin (p/12) = (6�+2�) / 2.
C. cos (p/12) = (6�+2�) / 2 et sin (p/12) = (6�-2�) / 2.
D. cos (p/12) = (6�+2�) / 4 et sin (p/12) = (6�-2�) / 4. Vrai.
z = exp( i p / 12) =cos (p/12) + i sin (p/12) = ( 2�+6�) +i(6�-*2� )] / 4.
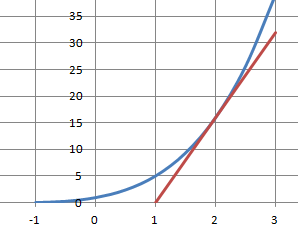
Question 15.
Soit f une fonction r�elle � variable r�elle d�finie par :
f(x) = (0,5 x+1)4.
L'�quation de la tangente � la courbe repr�sentative de la fonction f au point d'abscisse 2 est :
A.y = 16(x-2).
B. y = 8(x-1).
C. y = 8(x-2).
D. y = x-1.
f '(x) = 4 *0,5 (0,5 x+1)3 = 2(0,5 x+1)3 .
f '(2) =16, coefficient directeur de la tangente en x =2.
f(2) =16.
Equation de la tangente y = 16x +b ;
le point de coordonn�e (2 ; f(2)) appartient � la tangente :
16 = 16 *2+b ; b = -16.
y = 16x-16.
E. Aucune des r�ponses propos�es.
|
|
|
|
