Mathématiques,
concours TSEEAC technicien supérieur de l'aviation civile 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Partie I.
Une
étude montre que l'âge en mois auquel apparaissent les premiers mots de
vocabulaire chez un enfant pris au hasard dans la population peut se
modéliser par une variable aléatoire suivant la loi normale N(11,5 ;
16).
On donne pour une variable aléatoire X suivant la loi normale centrée réduite :
P(X < 2) = 0,977 ; P(X < 0,5) =0,691 ; P(X < 0,125) = 0,550 ; P ( X < 0,03125) =0,512.
Question 1.
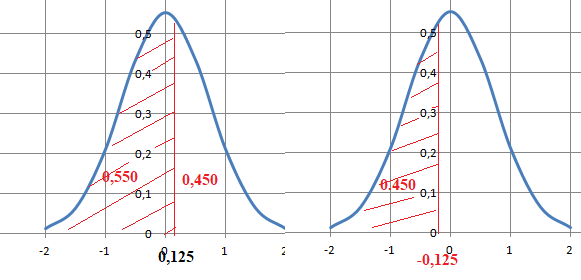
La probabilité p1 qu'un enfant de cette population ait prononcé ses premiers mots avant ses 9 mois et demi est d'environ :
A. 0,050 ; B. 0,161 ; C. 0,309 ; D. 0,450, vrai.
P(X < 9,5) ; Y =(9,5 -11,1 ) / 16 = -0,125 ; P(Y < -0,125) =1-P(Y < 0,125) =1-0,550 = 0,450.
 Question 2.
Question 2.
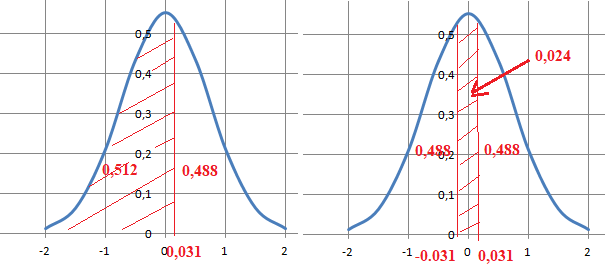
La probabilité p2 qu'un enfant de cette population ait prononcé ses premiers mots dans le cours du 12ème mois est d'environ :
A. 0,01 ; B. 0,024.
Vrai. C. 0,512. D. 0,550.
11 < X < 12 ; Y =(11-11,5) / 16 =-1 /32 =-0,03125 ; P(Y<-0,03125) =1-0,512=0,488.
Y =(12-11,5) / 16 =1 /32 =0,03125 ; P(Y<0,03125) =0,512.
P(-0,03125 < Y < 0,03125)=P( 11 < X <12) =0,512-0,488 =0,024.
Question 3.
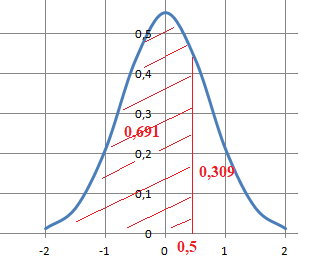
La probabilité p3 qu'un enfant de cette population ait prononcé ses premiers mots après l'age de 19 mois et demi est d'environ :
A. 0,023. B. 0,309 , vrai. C. 0,691. D. 0,977.
X >19,5 ; Y =(19,5 -11,5 ) / 16 = 0,5 ; P(Y > 0,5) = 1-P(Y < 0,5) = 1-0,691=0,309.
Partie 2.
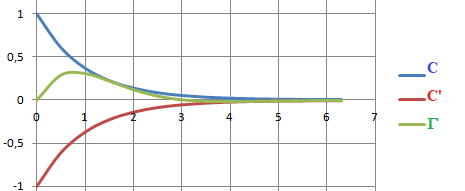
On considère sur [0 ; 2p] les courbes C d'équation y = e-x, C' d'équation y = -e-x et la courbe G représentant la fonction définie par f(x) = e-x sin x.
Question 4.
Les courbes vérifient :
A. La courbe G est au-dessous de C et C'.
B. La courbe G est au-dessus de C et C'.
C. La courbe G est au-dessus de C', mais oscille autour de C.
D. La courbe G est au-dessous de C, mais oscille autour de C'.
Comparer ex et e-x sin x :
ex > e-x sin x ; 1 > sinx est vrai. G est au-dessus de C.
Comparer -ex et e-x sin x :
-ex > e-x sin x ; -1 > sinx est faux. G est au-dessous de C'.
E. Toutes les propositions sont fausses.
Question 5.
La dérivée de la fonction f peut s'écrire :
On ppose u = e-x et v = sin x ; u' = -e-x ; v' = cos x.
f '(x) = u'v +v'u = -e-x sin x +e-x cos x = e-x ( cos x - sin x).
Réponse B.
Question 6.
La courbe G touche C au point d'abscisse :
e-x sin x = e-x ; sin x = 1 ; x = p /2.
Réponse A.
Question 7.
La tangente à G en ce point de contact admet pour équation :
y = ax +b ; a = f '(p/2) = - e-p/2.
Le point (p/2 ; e-p/2) appartient à la tangente : e-p/2 =-p/2e-p/2+b ; b = e-p/2(1+p/2).
y = - e-p/2 x + e-p/2(1+p/2).
Réponse B.
Partie III.
On
souhaite étudier une modélisation d'une tour de contrôle aérien,
chargée de surveiller deux routes aériennes représentées par deux
droites de l'espace. Le plan est rapporté à un repère orthonormé,
l'unité sur chaque axe est 1 km. Les deux routes sont représentées par
deux droites D1 et D2 dont on connait les représentations paramétriques.
D1 : x =3+a ; y = 9+3a ; z = 2 avec a réel.
D2 : x =0,5+2b ; y = 4+b ; z =4 -b avec b réel.
Question 8.
Les deux droites sont :
A. parallèles ; B. sécantes ; C. coplanaires. D. non coplanaires. Vrai.
Si les droites sont sécantes : 3+a = 0,5 +2b et 9+3a = 4+b soit b = 9+3a-4 =5+3a.
3+a =0,5 +10 +6a ; 5a = -7,5 ; a =-1,5 ; par suite b =0,5.
z=2 = 4-b donne b = 2 différent de 0,5.
Donc les droites ne sont pas sécantes.
Vecteur directeur de D1 :(1 ; 3 ; 0).
Vecteur directeur de D2 :(2 ; 1 ; -1).
Ces deux vecteurs n'étant pas colinéaires, les droites ne sont pas parallèles.
Ces droites n'étant ni parallèles, ni sécantes, elles ne sont pas coplanaires.
Question 9.
On veut installer au sommet S(3 ; 4 ; 0,1) de la tour de
contrôle un appareil de surveillance qui émet un rayon représenté par
une droite notée (R). Un technicien souhaite savoir s'il est possible
de choisir la direction de (R) pour que cette droite coupe chacune des
droites D1 et D2. Le point S vérifie :
A. S appartient à D1.
B. S appartient à D2.
C. S appartient à (R). Vrai.
D. S n'appartient à aucune de ces droites.
Si S appartient à
D1 : 3 =3+a soit a = 0 ; 4 diffère de 9+3a ; z = 2diffère de 0,1 : S n'appartient pas à D1.
Si S appartient à D2 : 3 =0,5+2b soit b =1,25 ; 4 diffère de 4+b ; S n'appartient pas à D2.
Question 10.
Soit P1 le plan contenant S et D1 et P2 le plan contenant S et D2. Les deux plans se coupent suivant la droite D.
A. Les droites D1 et D sont sécantes. Vrai.
B. Les droites D1 et D sont parallèles.
C. Les droites D2 et D sont sécantes. Vrai.
D. Les droites D2 et D sont parallèles.
D1 : coordonnées d'un vecteur directeur ( 1 ; 3 ; 0) ; A(3 ; 9 ; 2 ) appartient à cette droite.
Coordonnées d'un vecteur normal au plan P1 : (3 ; -1 ; 0) par exemple.
Equation cartésienne de ce plan : 3x-y+d=0.
S(3 ; 4 ; 0,1) appartient à ce plan :9-4+d=0 ; d=-5.
P1 : 3x-y-5=0. (1)
D2 : coordonnées d'un vecteur directeur ( 2 ; 1 ; -1) ; B(0,5 ; 4 ; 4 ) appartient à cette droite.
Coordonnées d'un vecteur normal au plan P2 : (0 ; 1 ; 1) par exemple.
Equation cartésienne de ce plan : y+z +d=0.
S(3 ; 4 ; 0,1) appartient à ce plan :4+0,1+d=0 ; d=-4,1.
P2 : y+z-4,1=0. (2).
Equation paramétrique de la droite D :
(1) donne : y =3x-5.
(1)+(2) donne : 3x+z-9,1=0 ; z=-3x+9,1.
x= 0 +1*x ; y =-5+3x ; z=9,1-3x.
Coordonnées d'un vecteur directeur de la droite D : (1 ; 3 ; -3 ).
Le point (0 ; -5 ; 9,1) appartient à cette droite.
Question 11.
Les droites (R) et D :
A. Ont un unique point d'intersection S.
B. Se coupent en un point distinct de S.
C. Sont confondues. Vrai.
D. Sont parallèles distinctes.
Equation paramétrique de la droite D : x= 0 +1*t ; y =-5+3t ; z=9,1-3t avec t réel.
S(3 ; 4 ; 0,1) appartient-il à cette droite ?
Si oui : t=3 ; y =-5+9=4 ; z=9,1-3*3=0,1.
S appartient à la droite D.
S appartient à la droite D et à la droite D1.
S appartient à la droite D et à la droite D2.
Les droites (R) et D sont confondues.
|
...
|
....
|
Partie IV.
On
considère une épreuve de Bernoulli de para mètre p. On répète cette
épreuve de façon identique et indépendante au maximum n fois et on
s'arrête à la réalisation du premier succès. La variable aléatoire X
prend :
la valeur 0 si aucun succès n' a été rencontré,
la valeur k si le premier succès est rencontré lors de la k-ième répétition.
Question 12.
On montre que :
A. P(X=0)=pn ; B. P(X=0)=(1-p)n, vrai ; C. P(X=k)=p(1-p)k-1 ; D. P(X=k)=pk(1-p)n-k.
P(X=0)=(n n)p0 (1-p)n =(1-p)n.
P(X=k)=(n k)pk (1-p)n-k .
Question 13.
L'espérance E(X) s'écrit :
A. E(X) = np vrai ; B. E(X) = n(1-p). C. E(X) = np(1-p). D. E(X) = p(1+2(1-p)+3(1-p)2+...n(1-p)n-1)).
On introduit la fonction f définie sur R par : f(x) = x+x2+x3+...+xn.
Question 14.
E(X) vérifie :
A. E(X) = f(p) ; B. E(X) = f(1-p). C. E(X) = pf '(1-p) vrai. D. E(X) = (1-p) f '( p).
k = 1 : P(X=1) = p; P(X=0)=1-p.
k=2 : P(X=2) = p(1-p) ; E(X) =p+2p(1-p)=3p-2p2=p(3-2p).
f '(1-p)=1+2(1-p)=3-2p.
Question 15.
Pour x différent de 1 :
A. f(x) =(1-xn+1) / (1-x) ;
Si n = 1 : f(x)=x ; (1-x1+1) / (1-x)=(1-x)(1+x) /(1-x) = 1+x diffère de x.
B. f '(x) =(1-xn(1+n-nx) / (1-x)2.
Si n = 1 : f '(x)=1 ; 1-x1(1+1-x) / (1-x)2=1-x(2-x) / (1-x)2diffère de 1.
C. E(x)=1 /(1-p) -pn/(1-p) -npn.
Si n =2 : E(x)=1 /(1-p) -p2/(1-p) -2p2=(1-p2) / (1-p) -2p2=1+p-2p2 diffère de 3-2p.
D. E(x) =1 /p -(1-p)n /p-n(1-p)n. Vrai.
Si n =2 : E(x)=1 / p -(1-p)2 /p-2(1-p)2=1 / p[1-(1+p2-2p)]-2(1+p2-2p)= -p+2-2-2p2+4p=3p-2p2=
|
|
|
|