Machine à
force de surface (SFA), mesure de déplacement, concours agrégation
interne
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Mesures de déplacement.
Pour
mesurer le déplacement relatif de la sphère et du plan, on fixe
rigidement la sphère et le plan à deux disques de duralumin de surface
S qu’on approche à une distance e l’un de l’autre en prenant garde au
parallélisme. On suppose que le condensateur, ainsi créé, ne perturbe
pas le fonctionnement du SFA.
2.1 Condensateur plan.
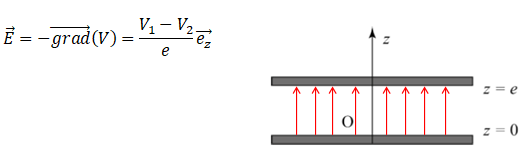
Un tel condensateur est représenté ci-dessous. On repère l’axe perpendiculaire aux faces du
condensateur par un axe Oz, de vecteur unitaire ez . Les dimensions du condensateur permettent de négliger les effets de bord.
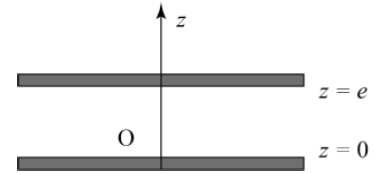
Considérons
que les deux plaques métalliques sont placées aux abscisses respectives
z = 0 et z = e et portées respectivement aux potentiels V1 et V2. Ces deux plaques forment un condensateur, c’est-àdire qu’elles portent respectivement les charges Q et −Q.
17. Rappeler les
équations de Maxwell vérifiées par les champs électrique et magnétique
dans le vide. Quelle équation permet de justifier qu’il est possible,
en électrostatique, d’écrire
le champ E sous la forme 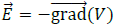
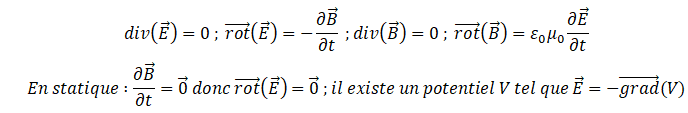
18. Etablir l’équation de Laplace vérifiée par le potentiel V(z) entre les plaques du condensateur.
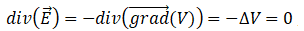
d2V / dz2 = 0.
19. Résoudre cette équation en utilisant les potentiels V1 et V2 et la distance e.
On intègre deux fois : V(z) = a z +b avec a et b des constantes.
V(0) =V1 = b.
V(e) = V2 = ae+V1 ; a = (V2-V1) / e.
V(z) = (V2-V1) z / e +V1.
20. En déduire une première expression du champ électrostatique E entre les 2 plaques à lʼaide de V1, V2 ete. Tracer, sur un schéma du condensateur, l’allure de quelques lignes du champ E. Préciser leur orientation en supposant V1 > V2.
21. Le champ étant
nul à l’extérieur, établir une deuxième expression du champ
électrostatique E entre les 2 plaques en fonction de Q, S et e0 la permittivité du vide.
Expression du champ électrique au voisinage d'un conducteur ( s : densité surfacique de charge).
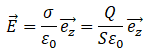
22. En déduire la capacité d’un tel condensateur plan.
(V1-V2) / e = Q / (S e0) ; C0 =Q /(V1-V2) = e0S / e.
2.2 Mesure du déplacement par capteur capacitif.
23. On assimile la permittivité diélectrique de l’air à celle du vide e0. Donner la valeur de C0 pour des disques de rayon R = 3,0 cm séparés par une distance e = 10 μm. Commenter la valeur obtenue.
C0 = 8,85 10-12 x 3,14 x 0,032 / 10-5 =2,5 10-9 F.
Cette valeur est très faible devant les capacités utilisées au lycée ( quelques microfarads).
24. Donner
l’expression de la force entre les armatures de ce condensateur si la
tension entre les bornes est maintenue fixe. Calculer la valeur de
cette force si la tension est maintenue à 5 V.
Energie électrique stockée dans le condensateur : E =½C0 U2=½e0S / z U2.
On dérive à tension U constante : F = -½e0S / e2 U2.
|F| =0,5 x8,85 10-12 x 3,14 x 0,032 / 10-10 x 52=3,1 10-3 N.
25. Etude du condensateur. Classe de terminale. Spécialité physique-chimie.
Un professeur souhaite étudier la charge d’un condensateur à travers un conducteur ohmique.
a. Schématiser le circuit électrique correspondant au montage.
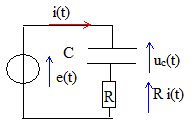
b. Expliciter la fonction du premier code Arduino fourni par le professeur.
void setup( ) {
pinMode(9, OUTPUT);
}
void loop( ) {
digitalWrite(9, LOW);
delay(5) ;
digitalWrite(9, HIGH);
delay(5);
}
Ce programme permet de délivrer une tension carrée e(t) de période T = 10 ms.
c. Indiquer comment
l’élève effectue le branchement sur le micro-controleur pour répondre
aux exigences du second code Arduino fourni.
La broche commune à C et R est reliée à A0 sur la carte arduino.
d. Expliquer la ligne de code « tension=valeur*5/1023 ».
Acquisition numérique allant de 0 à 1023 ( 1023 correspondant à 5 V).
x lue par la carte correspond à la tension 5 x / 1023.
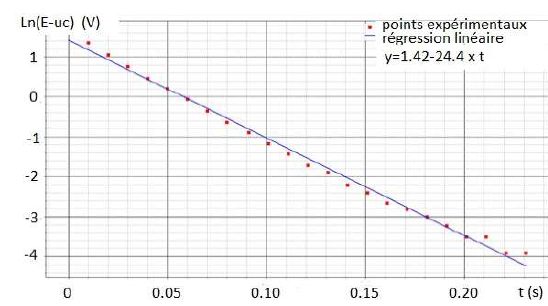
L’acquisition lors de la charge du condensateur permet de tracer la
courbe ln(5-tension) en fonction de t, ainsi que sa modélisation.
e.
Etablir l’expression donnée dans la question (3) de la partie «
exploitation ». Expliciter l’intérêt pédagogique de travailler avec
cette expression.
Exploitation :
1. Établir l’équation différentielle vérifiée par la tension uC aux bornes du condensateur lors de sa charge. On suppose le condensateur initialement déchargé.
Loi des mailles : E = R i(t) + uc(t) ; i(t) = dq(t) / dt = C duc/dt.
E =RC duc/dt + uc(t)
2. Déterminer la solution de l’équation différentielle, équation temporelle de la tension aux bornes du condensateur.
uc(t) = A exp(-t / RC) + E.
uc(t=0) = 0 = A+E soit A = -E.
uc(t) = E(1- exp(-t / RC).
3. Cette solution peut s’écrire également sous la forme :
E- uc(t) = E exp(-t / RC).
ln(E- uc(t)) = ln(E) - t / (RC).
On pose t = RC ; ln(E- uc(t)) = ln(E) - t / t.
La représentation logarithmique permet de trouver le temps caractéristique, le coefficient directeur de la droite étant -1 / t.
f.
Proposer une question utilisant le graphe obtenu pour répondre aux
exigences du programme. Formuler une réponse cohérente à cette question.
A partir du tracé de ln(E- uc(t)) en fonction du temps, retrouver la valeur du temps caractéristique de la charge de ce condensateur.
-1 / t = -24,4 s-1 ; t = 1 /24,4 =0,041 s.
Afin d’expliciter la notion d’équation différentielle et sa réalité
physique, le professeur envisage de l’aborder en activité expérimentale
de cours en représentant duc(ti)/dt en fonction de uc(ti). Dans un premier temps, à l’aide du microcontrôleur, il relève les valeurs de tensions successives.
Transférées dans un tableur, il détermine la dérivée de uc(ti) en calculant [uc(ti+1)-uc(ti)] /Dt.
g. Représenter duc(ti)/dt en fonction de uc(ti). Proposer un intérêt didactique de cette représentation.
Pour la charge : duc/dt = -1 / t (uc-E).
Pour la décharge : duc/dt = -1 / t uc.
Il existe un lien affine entre la fonction et sa dérivée. Le coefficient directeur étant -1 / t.
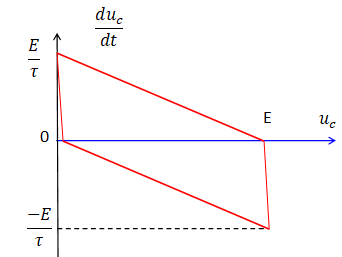
h. Quel intérêt scientifique présente le recours à un portrait de phase, c’est-à-dire une représentation duc(ti)/dt en fonction de uc(ti), lorsqu’on étudie un système dynamique ?
L'étude du système se fait sans calcul de la fonction ; on
détermine facilement le comportement asymptotique du système dynamique
selon les conditions initiales.
|
...
|
....
|
On
cherche à mesurer les variations de l’épaisseur e. Une méthode est de
transformer une mesure d’épaisseur en une mesure de fréquence beaucoup
plus précise. Pour ce faire, le principe consiste à réaliser un
oscillateur quasi-sinusoïdal dont la fréquence est reliée à l’épaisseur
e. Parmi les oscillateurs possibles, on peut imaginer d’utiliser un
oscillateur quasi-sinusoïdal dont le principe est représenté sur
la figure suivante. Ce circuit utilise un amplificateur linéaire
intégré, ou ALI, qui est un composant électronique dont l’alimentation
n’est pas représentée, considéré comme idéal et en régime linéaire. En
plus de l’ALI, le montage étudié comporte 3 résistances dont une
variable, la résistance R3.
On commence par étudier une partie du circuit représenté. Cette
sous-partie du circuit est représentée sur la figure ci-dessous. Pour
un ALI idéal en régime linéaire, on peut écrire que les intensités des
courants i+ et i− rentrant dans l’ALI sont nulles : i+ = i− = 0 et que
le gain est infini, conduisant, en régime linéaire, à v+ = v− .
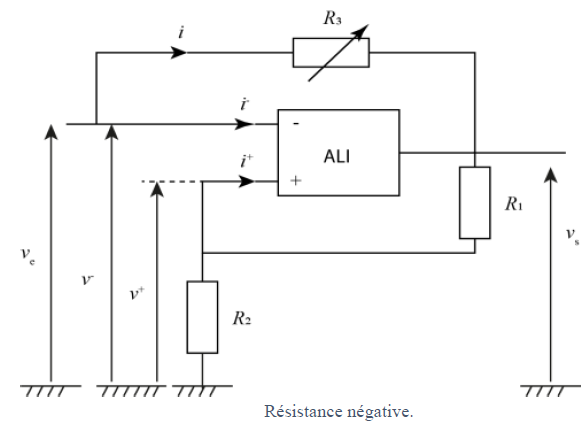
26. Rappeler les lois de Kirchhoff en électrocinétique.
Loi des noeuds : la somme des intensités des courants qui arrivent à un noeud est égale à la somme des intensités des courants qui en sortent.
Loi des mailles
: dans l'approximation des régimes quasistationnaires et à condition
que les varaitions de flux magnétique à travers cette maille soient
négligeables, la somme algèbrique des différences de potentiel le
long d'une maille est nulle.
27. Déterminer la relation liant ve, vs, R3 et i.
ve =vs +R3 i.
28. Déterminer la relation liant ve, vs, R1 et R2.
ve = v- =v+ et i+ = 0 ; ve= R2 i' ; vs=(R2+R1) i' ; ve= R2 / (R2+R1) vs.
29. En déduire que l’on peut écrire ve = Rn i où Rn est une grandeur négative homogène à une résistance, que l’on exprimera en fonction de R1, R2 et R3.
ve =vs +R3 i = (R2+R1) / R2 ve+R3 i.
ve [ 1- (R2+R1) / R2 ]=ve [ -R1 / R2 ] =R3 i.
ve= - R2 R3 / R1 i.
30. On place ce
montage en série avec une bobine d’inductance propre L et de résistance
interne r et le condensateur décrit précédemment de capacité C0 .
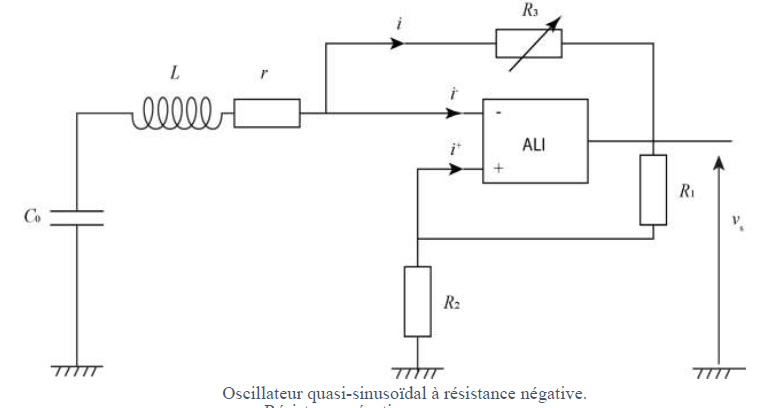
Établir une inégalité entre R1, R2 et R3
et r exprimant la condition pour laquelle on peut observer l’apparition
d’oscillations spontanées dans le circuit électrique. Exprimer la
fréquence f0 de ces oscillations en fonction de L et C0. Pour une valeur de L = 2,0 mH, calculer la valeur de cette fréquence de résonance pour la valeur de C0 =2,5 10-9 F.
uc + uL +(r+Rn)i = 0.
q / C0 +L di /dt +(r+Rn)i = 0.
i = dq /dt ; q / C0 +L d2q /dt2 +(r+Rn)dq / dt = 0.
On observe des oscillation si le coefficient d'amortissement est négatif ou nul : r+Rn < 0.
r < R2 R3 / R1.
Fréquence propre du circuit f0 :
d2q /dt2 +q / (LC0) =0 ; on pose w0 =1 /(LC0)½.
f0 = w0 / (2p)=1 / [ 2p(LC0)½].
f0=1 / [ 6,28 x(2 10-3 x2,5 10-9 )½]=7,1 104 Hz.
31. En général, les ALI ont des défauts. Citer deux défauts des ALI généralement rencontrés.
Impédance d'entrée non infinie ; saturation en courant et en tension ; courants de polarisation ; bande passante finie.
32. Connaissant l’expression de C0(e) qui a été rappelée à la question 22, établir la relation entre la variation de fréquence de résonance Df0 et la variation de distance De pour une variation De <<e : on exprimera Df0 en fonction de De, f0 et e. Déterminer l’incertitude-type acceptable
sur la mesure de f0 nécessaire pour mesurer la distance e avec une incertitude de 0,1 nm.
f0 = 1 / [ 2p(LC0)½] ; C0 = e0S / e.
f0 = 1 / [ 2p(Le0S / e)½]= k e½ avec k = 1 / [ 2p(Le0S )½].
Dérivée logarithmique : df0 / f0 =de / (2e).
Df0 / f0 =De / (2e).
Df0 =f0 De / (2e) =7,1 104 x 1 10-10 /(2 x 10-5) =0,35 Hz.
33. Lorsque les armatures se déplacent suivant une loi De = a cos(2pf1 t) avec f1 << f0 représenter l’allure du signal en sortie de l’oscillateur ? Citer une technique qui permet de mesurer a.
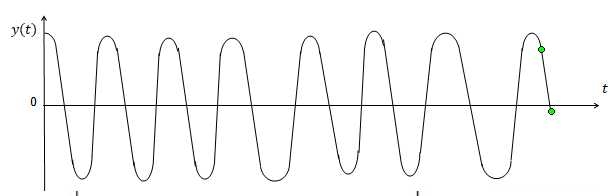
a peut être mesuré à l'aide d'un convertisseur fréquence tension.
Déplacement par céramique piézoélectrique
Dans le SFA le déplacement est assuré grâce à la céramique piézoélectrique.
35. Indiquer
l’identité du scientifique qui a découvert la piézoélectricité.
Expliquer en quelques mots le principe de la piézoélectricité. Citer
une application de la piézoélectricité disponible au laboratoire de
physique d’un lycée.
Pierre et Jacques Curie.
Certains matériaux se polarisent électriquement sous l'action d'une
contrainte mécanique et réciproquement il peuvent se déformer sous
l'action d'un champ électrique.
Au Lycée, les dispositifs à ultrasons utilisent la piézoélectricité.
|
|