Physique chimie, concours Puissance alpha 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
.. ..
......


...
Exercice 22 : Interf�rences lumineuses.
Un �l�ve r�alise une exp�rience d’interf�rences en �clairant deux fentes d’Young (deux fentes fines identiques verticales et parall�les) avec une source ponctuelle monochromatique de longueur d’onde 600 nm plac�e en S sur l’axe de sym�trie du syst�me. Les milieux des deux fentes S1 et S2 sont s�par�s d’une distance a.
La figure d’interf�rences (ci-dessous) est observ�e sur un �cran situ� � la distance D=1,5 m des fentes. Pour effectuer une mesure pr�cise de l’interfrange i, l’�l�ve mesure la distance L= 3,6 cm correspondant � 12 interfranges.
a) Dans cette exp�rience, la distance s�parant les deux fentes d’Young vaut a = 0,30 mm. Vrai.
i = L / 12 = 36 / 12 = 3 mm.
i = l D / a ; a = l D / i = 600 10-9 x1,5 / (3 10-3) =3 10-4 m = 0,30 mm.
. b) Sachant que la diff�rence de marche au point A  vaut d = 1,8 �𝑚, les ondes interf�rent, en ce point A, de mani�re constructive.Vrai.
d / l =1,8 10-6 /( 600 10-9) =3.

 L’�l�ve s’int�resse au point B sur l’�cran. Il mesure la distance s�parant le point B du centre O de la figure d’interf�rences et obtient OB= 4,5 cm.
 c) Au point B, les ondes issues des fentes S1 et S2 arrivent en opposition de phase. Faux.
OB / i = 45 / 3 = 15.
B est au centre d'une frange brillante. Les ondes issues des fentes S1 et S2 arrivent en  phase..
 d) Avec deux sources lasers identiques orient�es vers le point B, on n’observe pas le m�me r�sultat qu’avec le dispositif (source S + fentes d’Young). Vrai.
Les deux lasers ne sont pas des sources de lumi�res coh�rentes, condition n�cessaire pour obtenir des interf�rences..
Exercice 23 : �change au volley ball .
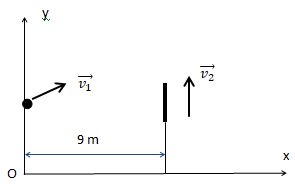
Au cours d’une s�ance d’entrainement, un joueur de volley ball frappe le ballon, de 21 cm de diam�tre, alors que le centre d’inertie de ce dernier se trouve � une hauteur de h = 2,0 m du sol. Il lui communique une vitesse v1 repr�sent�e sur le sch�ma ci-dessous. Au m�me moment, situ�e � 1,0 m du filet, la d�fenseuse adverse qui a anticip� l’action, prend une impulsion et s’�l�ve verticalement, avec une vitesse initiale v2 = 4,0 m / s. On supposera qu’avant le saut, son centre d’inertie se situe � 1,0 m du sol.
 On n�gligera toute action de l’air. g = 10,0 m s-2.

a) Apr�s avoir quitt� la main du volleyeur, le ballon a un mouvement de chute libre.Vrai.
Le ballon n'est soumis qu'� son poids ( action de l'air n�glig�e).
 b) Le mouvement est acc�l�r� le long de l’axe Ox. Faux.
Le poids �tant vertical, la seconde loi de Newton s'�crit selon OX : ax = 0.
Vitesse selon Ox : vx = constante.
 Les �quations horaires du ballon sont : x(t) = 20 t ; y(t) = -5,0 t2+4,5 t +2,0.
 L’�quation de sa trajectoire est : y(x) = − 0,0125  x2 + 0,225 x + 2,0.
 c) Lorsque le ballon arrive au niveau de la d�fenseuse adverse, son centre d’inertie se situe � 3,0 𝑚 du sol. Vrai.
x = 10 ; y =-0,0125 * 100 +0,225 x10 +2,0 = -1,25 +2,25 +2 = 3,0 m
 d) La d�fenseuse, ayant toujours l’extr�mit� de ses doigts 1,0 m au dessus de son centre d’inertie, r�ussit � intercepter le ballon. Faux.
Abscisse du ballon : x = 10 = 20 t ; t =0,5 s.
 Doigts de la d�fenseuse : y = -5t2 +v2t+2 = -5t2 + 4t+2 =-5 *0,25 + 4  = 2,75 m.
Rayon du ballon :0,105 m.
2,75 +0,105 < 3,0.
Excecice 24 : bilan d'�nergie thermique.
On souhaite construire un mur ext�rieur d’une maison en brique. Il sera sans ouverture (sans porte ni fen�tre). L’aire de sa surface doit �tre �gale � 60 m2. Sans isolation, il est pr�vu que l’�paisseur de brique soit de 20 cm.
 La temp�rature int�rieure de la maison sera maintenue constante � 20�C gr�ce � un chauffage �lectrique qui doit compenser le flux thermique � travers le mur. On se place dans la situation o� la temp�rature ext�rieure est de 0�C. On note par ailleurs que 1 kWh d’�nergie �lectrique fournie par EDF co�te environ 0,10 €.
On souhaite isoler le mur pour diminuer les d�perditions thermiques. Pour cela, on consid�re deux techniques d’isolation :
 1 �re technique : on accole au mur en brique de 20 cm une �paisseur de polystyr�ne de 4,0 cm.
2 �me technique : Le mur est construit avec deux parois de briques de 10 cm chacune, s�par�es par une couche d’air de 4 cm.
a) La r�sistance thermique du mur en brique sans isolation est de 5 � 10−3 K W−1. Vrai.
lbrique = 0,67 W m-1 K-1.
R�sistance thermique Rth = e / (l S) =0,20 /(0,67 *60) ~ 5 � 10−3 K W−1.
 b) Sans isolation, dans les conditions �voqu�es dans l’�nonc�, il faudra payer � EDF environ 6 € par jour pour compenser la perte d’�nergie � travers ce mur. Faux.
Flux thermique � travers le mur : DT / RTh =20 / (5 10-3) = 4,0 103 W.
Energie correspondante :4 103 x 24 =96 103 Wh = 96 kWh.
D�pense journali�re : 96 x 0,10 =9,6 €.

 c) La r�sistance thermique du mur isol� selon la premi�re technique d’isolation (avec le polystyr�ne) sera �gale � 2,5 � 10−2 K W−1 . Vrai.
lpoly = 0,033 W m-1 K-1.
 Rth = ebrique / (lbrique S) + epoly / (lpoly S)=0,20 /(0,67 *60) +0,04 /(0,033 x60)~ 5 � 10−3 + 2 10-2 ~2,5 10-2 K W−1.
 d) La premi�re technique d’isolation est plus efficace que la seconde. Faux.
lair = 0,025 W m-1 K-1.
 Rth = ebrique / (lbrique S) + eair / (lair S)=0,20 /(0,67 *60) +0,04 /(0,025 x60)~ 5 � 10−3 + 2,7 10-2 ~3,2 10-2 K W−1.

Exercice 25. La plan�te Mars.
La plan�te Mars est la quatri�me plan�te la plus proche du Soleil. Elle pr�sente un diam�tre de 6800 km environ et effectue une r�volution autour du Soleil en 687 jours, soit approximativement 2 ans. La plan�te rouge tourne sur elle-m�me en 24h 37 min et sa masse est trois millions de fois plus faible que celle du Soleil.
On rappelle que la p�riode de r�volution T d’une plan�te, d�crivant une orbite de demi grand axe a autour du Soleil v�rifie la loi de Kepler
T2 / a3 = 4 p2 / (GMS) o� MS est la masse du Soleil.
 Masse de la Terre : 6 � 1024𝑘𝑔 . Distance Terre-Soleil : 1,5 � 1011𝑚 = 1 unit� astronomique (ua)
- P�riode de r�volution de la Terre : 1 an ≈ 3 � 107 𝑠 . Constante universelle de gravitation : 𝐺 = 7 � 10−11 𝑁. 𝑚2 . 𝑘𝑔−2 .
 1,62 = 2,6 ; 1,6 3 = 4 ; 1,52 = 2,25 ; 1,5� 1,6 = 2,4 ; 1,5 3 = 3,4 ; p = 3.
 a) D’apr�s la deuxi�me loi de Kepler, le rayon soleil-plan�te balaie des aires �gales pendant des dur�es �gales � certaines positions bien pr�cises sur l’orbite. Faux.
 b) Si l’on consid�re la trajectoire de Mars dans le r�f�rentiel h�liocentrique comme circulaire, le rayon de son orbite vaut environ 2,4 � 1011 𝑚. Vrai.
T2mars / a3mars = T2terre / a3terre ; a3mars = T2mars / T2terre a3terre = (687 / 365)2 x13 =3,54 u.a3.
amars =1,5 ua =1,5 x 1,5 1011 ~2,4 1011 m.

 c) La masse de Mars vaut environ 2 � 1030 kg. Faux.
T2terre / a3terre  = (3,7107)2 / (1,5 1011)3 =4 10-19.
4 10-19 =4 p2 / (GMS) ; MS= 32 /(10-19 x7 10-11)~1,3 1030 kg.
masse de mars : 1,3 1030 /( 3 106)~4 1023 kg.

 d) Une plan�te situ�e quatre fois plus loin du Soleil que Mars, aurait une p�riode de r�volution d’environ 16 ans.
T2 / a3 = constante. Vrai.
Si a est multipli� par 4, a3 est multipli� par 64 et T est multipli� par 8.
687 / 365 ~1,9 ans ; 1,9 x 8 ~ 16 ans.



....

 Exercice 26. Etude cin�tique par spectrophotom�trie.
Le diode dispose de propri�t�s antiseptiques mises � profit pour d�sinfecter des plaies ou br�lures superficielles, on le retrouve ainsi dans l’eau iod�e ou dans la b�tadine. On se propose ici d’�tudier la cin�tique de la r�action permettant de former du diiode I2 � partir des ions iodure I- et des ions peroxodisulfate 𝑆2𝑂8 2− � l’aide d’un suivi par spectrophotom�trie. L’�quation de la r�action mod�lisant cette transformation totale est :
 2𝐼 −(aq) + 𝑆2𝑂8 2−(𝑎𝑞) --> 𝐼2 (𝑎𝑞) + 2𝑆𝑂4 2−(𝑎𝑞).
 Le diiode est la seule esp�ce color�e. A l’instant initial, on r�alise un m�lange � partir d’un volume 𝑉1 = 10,0 mL de solution d’iodure de potassium ( 𝐾 +(𝑎𝑞) + 𝐼 −(aq) ) de concentration 𝐶1 = 5,0 � 10−1𝑚𝑜𝑙. 𝐿 −1 et d’un volume 𝑉2 = 10,0 𝑚𝐿 de solution de peroxodisulfate de sodium (2𝑁𝑎+(𝑎𝑞) + 𝑆2𝑂8 2−(𝑎𝑞)) de concentration 𝐶2 = 4,0 � 10−3𝑚𝑜𝑙. 𝐿 −1 . La longueur d’onde du spectrophotom�tre est r�gl�e sur la valeur correspondant � l’absorption maximale par le diiode. La loi de Beer Lambert nous permet d’�crire ici : 𝐴 = 400 � [𝐼2 ] 𝑎𝑣𝑒𝑐 [𝐼2 ] 𝑒𝑛 𝑚𝑜𝑙. 𝐿 −1 . 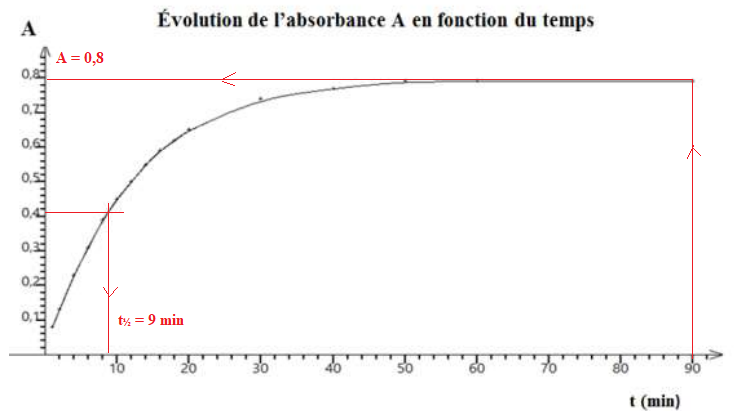On obtient la courbe ci-dessous :

a) La r�action qui se produit est une r�action d’oxydor�duction. Vrai.
Oxydation de I- : 2I- --> I2+2e-.
R�duction de 𝑆2𝑂8 2− : 𝑆2𝑂8 2−(𝑎𝑞)+2e- -->  2𝑆𝑂4 2−(𝑎𝑞).
 b) La quantit� de diiode produite apr�s 90 𝑚𝑖𝑛 vaut environ 40 𝑚𝑚𝑜𝑙. Faux.
[I2] = A / 400 = 0,8 / 400 =0,002 mol / L = 2 mmol / L dans un volume de 20 mL
Soit 2 x20 / 1000 =0,04 mmol.
 c) Le temps de demi-r�action vaut environ 30 𝑚𝑖𝑛. Faux.
 d) En utilisant une solution d’iodure de potassium plus concentr�e, on formera davantage de diiode � la fin de la transformation. Faux.
Quantit� de mati�re initiale : n(I2 ) =C1V1 = 0,5 x 10 = 5 mmol.
n(𝑆2𝑂8 2− ) =C2V2 = 4 10-3 x 10 = 0,04 mmol.
n(𝑆2𝑂8 2− ) / 1 =0,04 mmol ; n(I2 ) / 2 = 2,5 mmol ( en exc�s).

Exercice 27. Aspirine 500.
L’aspirine est un m�dicament antipyr�tique, anti-inflammatoire et analg�sique. Il est �galement utilis�, sous faible dosage, pour ses propri�t�s anticoagulantes. Son principe actif est l’acide ac�tylsalicylique, dont la mol�cule est repr�sent�e ci-dessous. Il fait partie d’un couple acide/base qui sera repr�sent� dans la suite de l’exercice par 𝐴𝐻/𝐴 −. Le technicien � qualit� � d’une firme pharmaceutique est charg� de contr�ler la qualit� du produit synth�tis� par son entreprise et doit en particulier v�rifier l’indication � Aspirine 500 �. Pour cela, il broye un comprim� d’aspirine 500 qu’il dissout ensuite dans un volume 𝑉 d'eau distill�e. Puis il r�alise un titrage suivi par pHm�trie de la solution S obtenue par une solution d’hydroxyde de sodium (𝑁𝑎+(𝑎𝑞) + 𝐻𝑂 −(𝑎𝑞)) ) de concentration en solut� apport� 𝐶𝑏 = 2,0 � 10−1 𝑚𝑜𝑙. 𝐿 −1 . L’�quation de la r�action support du titrage est : 𝐴𝐻(𝑎𝑞) + 𝐻𝑂 −(𝑎𝑞) --> 𝐴 −(𝑎𝑞) + 𝐻2𝑂(𝑙)
Ci-dessous, quelques informations port�es sur la boite du m�dicament :
Principe actif acide ac�tylsalicylique 500 mg par comprim�. Excipients amidon de ma�s, poudre de cellulose granul�e.
- Masse molaire de l’aspirine : 𝑀(𝑎𝑠𝑝𝑖𝑟𝑖𝑛𝑒) = 180 g.mol-1
- Solubilit� de l’aspirine dans l’eau � 25�C : 𝑠 = 3,3 𝑔. 𝐿 −1.
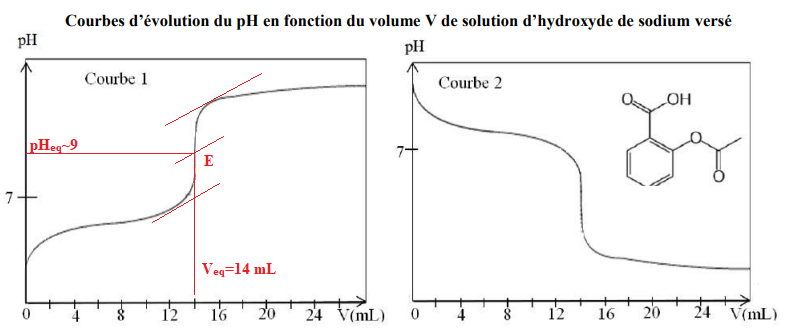
Le technicien obtient l’une des courbes suivantes :

a) Le technicien peut utiliser une fiole jaug�e de 100 𝑚𝐿 pour effectuer sa dissolution. Faux.
Solubilit� 3,3 g / L soit 0,33 g= 330 mg dans 100 mL.
 b) Le technicien obtient la courbe 2. Faux.
. c) Le technicien choisit la ph�nolphtal�ine (zone de virage 8,2 ; 10 )comme indicateur color� : l’�quivalence est rep�r�e par le passage de l’incolore au rose. Vrai.

 d) Le technicien obtient la m�me indication que celle indiqu�e sur la boite � moins de 1% pr�s. Vrai.
Quantit� de mati�re � l'�quivalence : Cb V�q =0,20 x 14 = 2,8 mmol.
Masse d'aspirine : 2,8 x 180 = 504 mg.
Ecart relatif : (504-500) / 500 = 0,008 ( 0,8 %).

Exercice 28 : Dosage par conductim�trie.
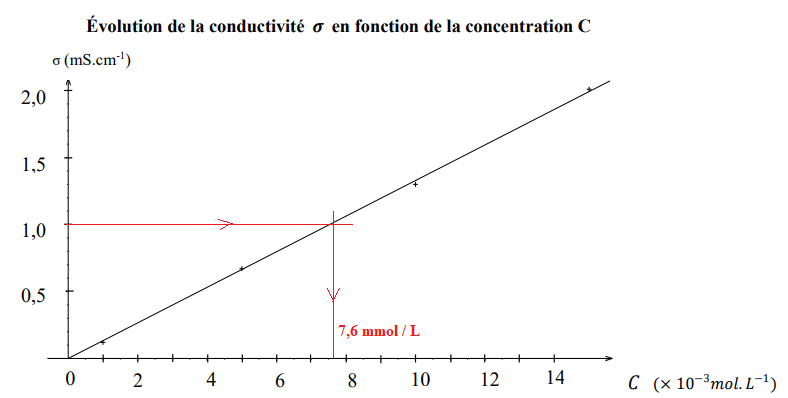
On souhaite v�rifier la concentration en chlorure de sodium d’une dosette de 5,0 mL de s�rum physiologique � l’aide d’un dosage par �talonnage suivi par conductim�trie. Le s�rum physiologique �tant trop concentr� pour le conductim�tre, il est n�cessaire au pr�alable de le diluer 20 fois. On obtient alors une solution appel�e solution S, dont la conductivit� vaut s = 1,0 mS. cm−1 . A l’aide de plusieurs solutions �talons de chlorure de sodium (de concentration connue), on trace la courbe d’�talonnage suivante :

a) La dilution du s�rum physiologique contenu dans toute la dosette peut se faire � l’aide d’une fiole jaug�e de 50,0 𝑚𝐿. Faux.
Volume de la fiole jaug�e : 20 x volume dosette =20 x 5,0 = 100 mL.
 b) La solution S a une conductivit� �gale � 0,10 𝑆. 𝑚−1 . Vrai.
1,0 10-3 / 10-2 =0,1 S m-1.
 c) Il est conseill� de ne plus utiliser le s�rum physiologique �tudi� car sa concentration massique est inf�rieure � 8,0 𝑔. 𝐿 −1 . Faux.
C = 7,6 mmol / L ; M(NaCl) = 23 +35;5 = 58,5 g / mol.
7,6 x 58,5 =444,6 mg / L ~ 0,44 g / L.
Tenir compte de la dilution : 20 x 0,4446 ~8,9 g / L

 d) La mesure peut �tre consid�r�e comme satisfaisante. Vrai.
La composition du s�rum physiologique est extr�mement simple. Il s’agit d’eau distill�e st�rile, dans laquelle du chlorure de sodium (𝑁𝑎𝐶𝑙) a �t� dissout, � hauteur de 0,9% en masse.
Ecart relatif ( 9 -8,9 ) / 9 ~0,011 ( 1,1 %)
Cette valeur �tant inf�rieure � 5 %, c'est satisfaisant.

  
menu