Math�matiques, Concours EMIA, �cole militaire interarmes 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
.. ..
......


...
Exercice 1 : calculs alg�briques.
Les questions suivantes sont ind�pendantes.
1. Soient deux r�els a, b strictement positifs ; simplifier :

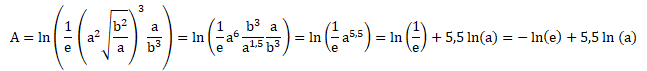
2. Simplifier :

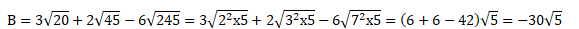
3. D�terminer les parties r�elles et imaginaires du nombre complexe :
z = 2 x 3� exp(-ip/3).
z = 2 x 3� (cos (-p/3) + i sin (-p/3)) = 2 x 3� ( 0,5 -i 3� /2) = 3� -3i.

4. Calculer et simplifier :


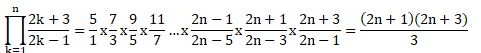
Exercice 2. D�riv�es et primitives.
1. Calculer les d�riv�es des fonctions suivantes.
f(x) = ex / x.
On pose u = ex et v = x ; u' = ex ; v' = 1.
(u'v-v'u) / v2 =(exx -ex) / x2 = ex(x-1)/x2.
f(x) = cos (x)5.
On pose u = x5 ; u' = 5 x4 ; f '(u) = -u' sin (u) =-5 x4  sin (x)5.
f(x) = x exp(x�+1).
On pose u = x et v = exp(x�+1) ; u'  =  1 ; v' =0,5 x-�exp(x�+1).
u'v+v'u = exp(x�+1) +0,5 x�exp(x�+1) = exp(x�+1)(1+0,5 x�).

2. Calculer une primitive pour chacune des fonctions suivantes.
f(x) = 1 /x� = x-�. F(x) = 2 x�.
f(x) = ex(ex+1)3.
On pose u = ex+1 ; u' = ex ;  f(u) =u' u3 ; F(u) = u4 / 4 =(ex+1)4 / 4.
f(x) = x2 /(x+1).
Exprimer f(x) sous la forme ax+b+c / (x+1).
R�duire au m�me d�nominateur : (ax2+ax+bx+b+c) / (x+1).
On identifie : a = 1 ; a+b = 0 soit b = -1 ; b+c = 0 soit c =1.
f(x) = -1+x + 1/(x+1) ;
F(x) = -x +0,5x2+ln(x+1).

 3. Calculer l'int�grale suivante ( int�gration par parties).
On pose u' = x2 ; v=ln(x) ; u = x3 / 3 ; v' = 1 /x.

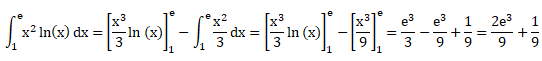
Exercice 3. R�solution d'�quations.
1. R�soudre dans R l'�quation suivante :
e2x+3ex=4.
On pose X =ex >0.
X2+3X-4=0 ; discriminant D =32+16=25 = 52.
Solution positive retenue : X = (-3+5) / 2 = 1 ; x = 0.
2. R�soudre dans R l'�quation suivante : |2x+3| =5.
Si x > -1,5 : 2x+3 =5 ; x = 1.
Si x > -1,5 : -(2x+3) =5 ; x = -4.
 3. R�soudre le syst�me :
x+2y-z=1
x-y+z=2
xyz=0.
La troisi�me conduit � : x=0 ou y = 0 ou z = 0.
La somme des deux pemi�res donne  : 2x+y = 3.
La diff�rence des deux pemi�res donne  : 3y-2z = -1.
Si x = 0 ; y = 3 ; z = 5.
Si y = 0 ; x=1,5 ; z = 0,5.
Si z = 0 ; y = -1 /3 ; x =5 /3.

Exercice 4. Calcul matriciel.
On consid�re les matrices :

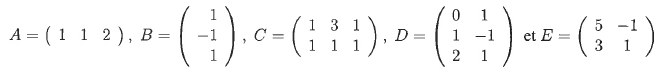
Pour chacune des affirmations ou r�ponses suivantes, r�pondre VRAI ou FAUX sans justifier.
1. A+B = B n'existe pas. Vrai.
L'addition de matrices n'est possible que lorsque les matrices ont le m�me nombre de lignes et le m�me nombre de colonnes.
2. AB =(2). Vrai.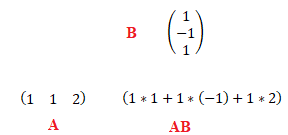
3. CA = (62). Faux.
Le produit d'une matrice A par une matrice C est possible si et seulement si le nombre de colonnes de la matrice A est �gal au nombre de lignes de la matrice C.
4. CD = E. Vrai.

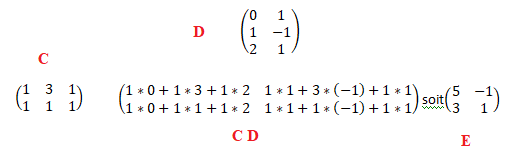
Exercice 5. Logique.
Pour chaque proposition suivante, donner leur n�gation.
1. " Pour tout x r�el, f(x) diff�re de z�ro".
 Il existe au moins un r�el x pour lequel f(x) = 0.
2. Soit x r�el : si f(x) < 0, alors x > 0.
Si f(x) < 0, alors x < 0.

Exeercice 6. Etude d'une suite num�rique.
La suite (un) est d�finie pour tout entier naturel par :
un+1 = 0,4 un +3 et u0 = -1.
On �tudie �galement la suite (vn) d�finie par : vn = 5-un.
1. D�montrer que vn = 6x(0,4)n.
v0 =5-u0=5-(-1)= 6.
vn+1 = 5-un+1= 5-(0,4 un +3)=2-0,4 un= 0,4( 5-un)= 0,4 vn.
(vn) est une suite g�om�trique de raison 0,4 et de premier terme v0 = 6.
Donc vn = 6x(0,4)n.
 2. D�terminer la limite de la suite (un).
-1 < 0,4 < 1, donc 0,4n tend vers z�ro si n tend vers plus l'infini.
vn tend donc vers z�ro et un tend vers 5.
3. D�terminer en fonction de n la somme v0 +v1 +... +vn.
Somme des termes d'une suite g�om�trique de raison 0,4 et de premier terme 6 :
6 (1-0,4n+1) / (1-0,4) =10(1-0,4n+1)
4. En d�duire en fonction de n la somme u0 +u1 +... +un.
un = 5-vn.
La somme u0 +u1 +... +un vaut : 5(n+1)-10(1-0,4n+1)

...
....

 Exercice 7. Polyn�mes.
Les questions suivantes sont ind�pendantes.
1. A(x) = 2x4 +3x3 -8x2-2x+1 et B(x) = x2+3x+1. Soit A = BQ+R la division euclidienne de A par B. D�terminer les polyn�mes Q et R.

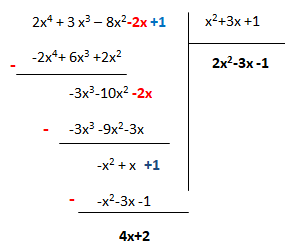
2 . Soit P(x) = x3+4x2-3x-18.
a. V�rifier que -3 est une racine de P(x) et du polyn�me d�riv�e P'(x).
P(-3) = (-3)3+4(-3)2-3(-3)-18 =-27+36+9-18=0.
P'(x) = 3x2 +8x-3. P'(-3) = 3(-3)2+8(-3)-3 =27-24-3=0.
b. Donner une expression factoris�e de P et donner l'ordre de la racine -3.
P(x) =(x-(-3))(x2+bx+c) =(x+3)(x2+bx+c).
On d�veloppe : x3 +(b+3)x2 +(c+3b)x +3c.
On identifie  : b+3 = 4 soit b = 1 ; c = -6.
P(x) =(x+3)(x2+x-6) .
Or x2+x-6= (x+3)(x-2).
P(x) =(x+3)2(x-2). -3 est une racine double.

 Exercice 8. G�om�trie.
Pour chacune des affirmations ou r�ponses suivantes, r�pondre VRAI ou FAUX sans justifier.
 1. Dans le plan muni d'une base orthonorm�e on consid�re les vecteurs suivants. Comment faut-il choisir a afin que 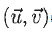soit une base orthonorm�e ?
La norme des vecteurs doit �tre �gale � 1 et les vecteurs doivent �tre orthogonaux. Les r�ponses a et b sont vraies.

 2. Dans le plan muni d'une base orthonorm�e on consid�re les vecteurs suivants de norme 3. L'angle form� entre ces vecteurs est p /3. Quelle est la norme de la somme des deux vecteurs.

La r�ponse c est vraie.
 3. On consid�re les points A(1 ; 1), B(-1 ; 1) et C(1 ; -1).

AB = 2 ; AC =2. AB2 = 4 ; AC2 = 4 ; BC2 =22+22=8. Le triangle ABC est isoc�le et rectangle en A.
Les r�ponses b et d sont vraies.
4. Soit P le plan passant par A(1 ; 1 ; 0) et de vecteur normal de coordonn�es 1 ; -1 ; 1).
Equation cart�sienne du plan x-y+z+d=0.
A appartient � ce plan : 1-1+0+d =0 soit d = 0
Equation cart�sienne de ce plan : x-y+z=0.
La r�ponse b est vraie.
5. Le cercle de centre A(1 ; 1) passant par B(2 ; 2) a pour �quation :
R: rayon du cercle R = AB2 =(2-1)2+(2-1)2 =2.
Equation du cercle : (x-1)2 +(y-1)2 = 2.
La r�ponse d est vraie.

Exercice 9. Equation et fonction.
On consid�re l'�quation d'inconnue x r�elle suivante : ln(1+|x| )= 1 /(x-1). (1)
On d�finit la fonction r�elle f (x) =ln(1+|x| )+ 1 /(1-x).
1. D�terminer l'ensemble de d�finition de la fonction f.
x-1 diff�rent de z�ro soit x diff�rent de 1.
1+|x|  > 0.
Si x est n�gatif, |x| = -x ; 1-x > 0 est bien v�rifi�.
Si x est positif, |x| = x ; 1+x >0 est bien v�rifi�.
Domaine de d�finition  : ]-oo ; 1[ union ]1 ; +oo[.
2. La fonction f est-elle d�rivable en z�ro ? Justifier.
Si x < 0 : f (x) =ln(1-x )+ 1 /(1-x).
f '(x)= - 1/(1-x)+1/(1-x)2.
Si x tend vers 0- : f '(x) tend vers 0.
Si x > 0 : f (x) =ln(1+x )+ 1 /(1-x).
f '(x)=1/(1+x)+1/(1-x)2.
Si x tend vers 0+ : f '(x)  tend vers 2.
f(x) n'est pas d�rivable en z�ro.
3. Soit x r�elle, v�rifier que x est solution de l'�quation (1) si et seulement si f(x) = 0.
Si f(x) =0 : ln(1+|x| )+ 1 /(1-x)=0 soit ln(1+|x| )= -1 /(1-x)=1/(x-1).
Si ln(1+|x| )= 1 /(x-1) : ln(1+|x| )-1/(x-1) =0.
 ln(1+|x| )+1/(1-x) =f(x) = 0.
4. D�montrer que si x appartient � ]-oo ; 1 [, alors x n'est pas solution de (1).
Si x < 0 : f (x) =ln(1-x )+ 1 /(1-x) >0.
Si x appartient � [0 ; 1[ : f (x) =ln(1+x )+ 1 /(1-x) >0.
Sur ]-oo ; 1[, f(x) diff�re de z�ro : alors x n'est pas solution de (1).
5. Calculer la limite de f(x) en plus l'infini.
f (x) =ln(1+x )+ 1 /(1-x).
En plus l'infini : 1 / (1-x) tend vers z�ro ; ln(1+x) tend vers plus l'infini; f(x) tend vers plus l'infini.
 6. D�montrer que f est strictement croissante sur ]1 ; +oo[.
f '(x)=1/(1+x)+1/(1-x)2 < 0.
La d�riv�e �tant strictement positive sur cet intervalle, f(x) est strictement croissante sur 1 ; +oo[ de moins l'infini � ln(3)-1 ~0,0986.
7. En d�duire que (1) admet une unique solution a telle que 1 < a < 2.
D'apr�s le th�or�me de la bijection, f(x) = 0 admet une unique solution sur 1 ; +oo[ .


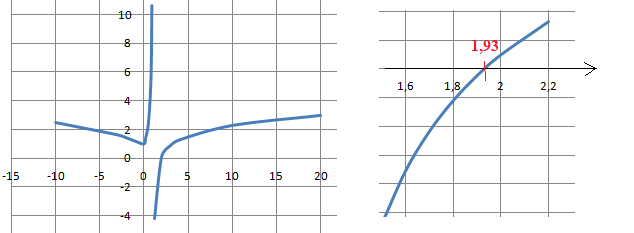
Exercice 10. Probabilit�s.
Quentin, Nicole et Lucie doivent r�pondre � u QCM comportant 4 questions. Pour chaque question une seule des 4 propositions A, B, C ou D est exacte. Une bonne r�ponse rapporte 1 point, une mauvaise enl�ve 0,5 point. l'absence de r�ponse n'apporte ni n'enl�ve aucun point.
Si le total des points est n�gatif, la note globale attribu�e � l'exercice est 0.
L'�l�ve recopie sur sa feuille une grille de r�ponses pr�sent�e comme suit :
Question
 r�ponse : A, B, C, D
1
2
3
4

On admet que les trois candidats r�pondent correctement � la premi�re question.
1. Quentin choisit de ne pas r�pondre � la question 2 et de donner une r�ponse des deux derni�res questions de mani�re ind�pendante en suivant la strat�gie suivante :   pour chaque question, il choisit au hasard, de fa�on �quiprobable l'une des 4 r�ponses propos�es.
a. Quelles notes peut-il obtenir � ce QCM ?
Les questions 1 et 2 lui rapportent 1 point.

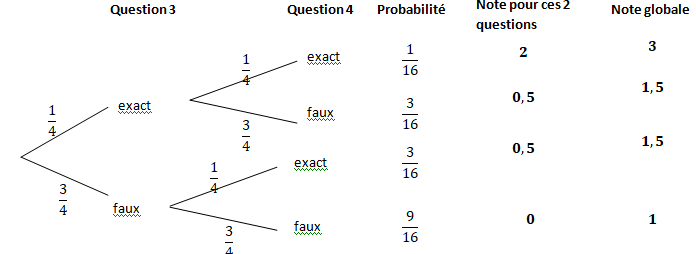
b. Combien de grilles diff�rentes peut-il remplir ? 44 grilles.
AAA ; AAB ; AAC ; AAD ; ABA ; ABB ; ABC ; ABD ; BAA ; BAB ; BAC ; BAD ; BBA ; BBB ; BBC ; BBD ; CAA ; CAB ; CAC ; CAD ; CBA ; CBB ; CBC ; CBD ; CCA ; CCB ; CCC ; CCD ; DAA ; DAB ; DAC ; DAD ; DBA ; DBB ; DBC ; DBD ; DCA ; DCB ; DCC ; DCD ; DDA ; DDB ; DDC ; DDD.
c. Quelle probabilit� a t-il de ne faire aucune faute ? 1 / 16
d. Quelle probabilit� a-t-il de faire 2 fautes ?  9 / 16
e. On note X la variable al�atoire donnant la note obtenue par Quentin. D�terminer la loi de X et calculer son esp�rance.
Note
 3
 1,5
 1
Probabilit�
 1 / 16
 6 / 16
 9 / 16
                     Esp�rance : (3 +1,5 x6 +9) / 16 =21 /16 =1,3125.
2. Nicole adopte la strat�gie de donner une r�ponse � chacune des trois derni�res questions de mani�re ind�pendante en choisissant au hasard, de fa�on �quiprobable, l'une des 4 r�ponses propos�es.

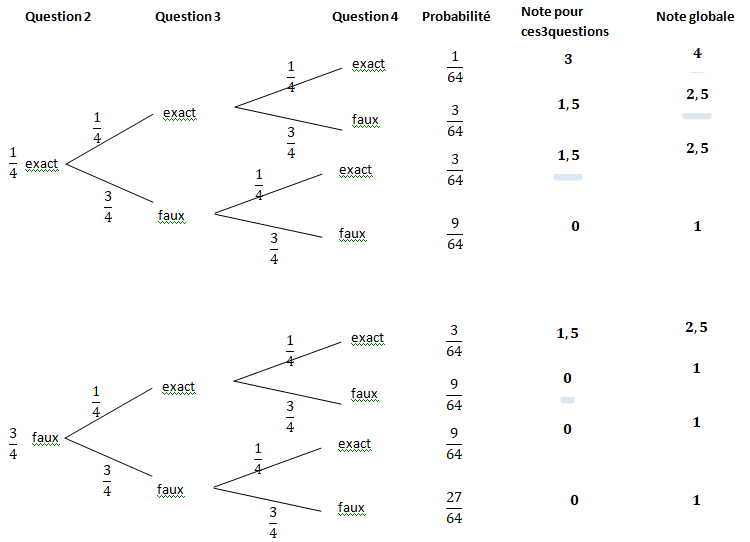
a. Quelle probabilit� a-t-elle de ne faire aucune faute ? 1 / 64.
b. Quelle probabilit� a-t-elle de faire 3 fautes ? 27 / 64.
c. On note Y la variable al�atoire donnant la note de Nicole. Calculer son esp�rance.
e. On note X la variable al�atoire donnant la note obtenue par Quentin. D�terminer la loi de X et calculer son esp�rance.
Note
 4
 2,5
 1
Probabilit�
 1 / 64
 9 / 64
 54 / 64
                     Esp�rance : (4 +2,5 x9 +54) / 64 =80,5 /64 ~1,28.
3. Lucie choisit de ne r�pondre � aucune des 3 derni�res questions. Classer les trois strat�gies.
Quentin (1,31) ; Nicole ( 1,28 ) ; Lucie (1).

 Analyse de processus.
On consid�re l'algorithme suivant :

 1. Appliquer l'algorithme au tableau R =[1 ; 3 ; 8 ; 3 ; 7] en donnant la valeur de D en sortie.
i
 1
 2
 3
j
 2
 3
 4
 3
 4
 4
D
 0
 0
 0
 0
 1
 0
2. Proposer un logigramme correspondant � cet algorithme.

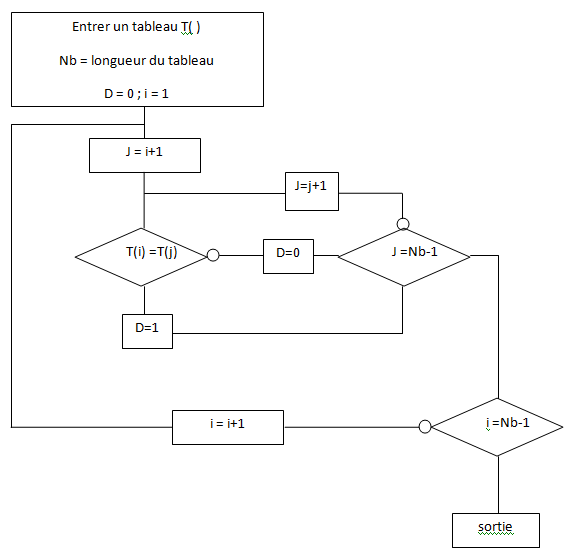
3. Expliquer le r�sultat donn� par cet algorithme appliqu� � un tableau de nombres entiers naturels quelconque.
Il rep�re dans le tableau la position des nombres identiques.

Exercice 12.
Ecrire en langage naturel un programme qui permet de sortir en affichage le dessin suivant :

i = 10 ; j = 1
Tant que i > 1
R�p�ter i fois
Ecrire 10-i
Fin r�p�ter
Passer � la ligne
R�p�ter j fois
Ecrire  "espace"
i = i-1 ; j = j+1
Fin Tant que

  
menu