Physique,
gaz parfait, circuit RC, microscope, QCM,
Concours ESA 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Exercice 1. (5,5 points).
2
moles d'hélium considéré comme un gaz parfait sont enfermées dans une
enceinte étanche aux parois indéformables. Le volume de l'enceinte est
ajustable par l'intermédiaire d'un piston.
1. Le volume de
l'enceinte est constant et vaut 10 L dans les questions 1 et 2.
a. Calculer la
masse d'hélium enfermée dans l'enceinte. M(He) = 4 g / mol.
m = 2 x 4 = 8 g = 8 10 -3 kg.
b. En déduire la
masse volumique de l'hélium.
masse (kg) / volume ( m 3) =8 10 -3 / 0,010 =0,8 kg
m -3.
c. A quelle
condition la masse volumique de l'hélium calculée en b reste constante
même si les conditions thermodynamiques P, T varient et que le volume
reste constant.
Le volume étant constant, la masse volumique reste constante si la
masse d'hélium reste constante.
2. A l'équilibre
thermodynamique, l'hélium atteint une température de 227 °C.
a. Calculer la température en kelvin.
227 + 273 = 500 K.
b. Calculer la
pression exercée par l'hélium.
P = n RT / V.
n = 2 moles ; R ~ 8 J K-1 mol-1 ; V = 0,010 m3.
P = 2 x 8 x500 / 0,01 = 8,0 105 Pa.
3. On
modifie la
position du piston et l'hélium subit une transformation à température
constante 227 °C et atteint à l'équilibre une pression finale de 200
kPa.
a. Quel est le
volume dans ces conditions ?
P V = cste.
8 10 5 x0,01 = 2 10 5 V ; V = 0,04 m 3.
b. Montrer que l'on
peut obtenir cette pression finale de 200 kPa en modifiant à la fois T
et V si la relation T / V = 12,5 103 usi est vérifiée.
Préciser l'unité de T / V.
P = n RT / V = 2 x8 T / V = 16 T / V = 2,0 105.
T / V = 2,0 105 / 16 =12,5 103 K m-3.
4. On déplace le
piston de manière lente d'une position initiale à une position finale.
Le gaz fournit un travail de 2,5 kJ au milieu extérieur et sa variation
d'énergie interne est nulle.
a. Rappeler
l'expression du premier principe de la thermodynamique en explicitant
toutes les grandeurs avec les unités.
DU = W
+ Q.
DU
: variation de l'énergie interne en joule.
Q : chaleur échangée (joule) entre le système et l'extérieur.
W : travail mis en oeuvre ( joule)
b. En déduire la chaleur échangée
au cours de cette transformation.
La variation
d'énergie interne est nulle. DU =0.
Q = - W avec W = -2,5 kJ ( le gaz fournit un travail au milieu
extérieur W < 0).
Q = 2,5 kJ.
c. On peut
montrer que la variation d'énergie interne pour un système compressible
comme l'hélium possède la même expression que celle d'un système
incompressible. En supposant que la capacité thermique de l'hélium est
constante au cours de la transformation, montrer que la transformation
est effectuée à température constante.
Le système étant incompressible, W = 0 et DU = Q = m c DT.
La variation
d'énergie interne étant nulle. DT =0.
Exercice 2. 5
points.
Soit un circuit RC série. Le condensateur est initialement déchargé et
à t = 0, l'interrupteur K est fermé reliant le générateur e(t) continu
de valeur E au reste du circuit. R = 10 kW et C = 1 µF.
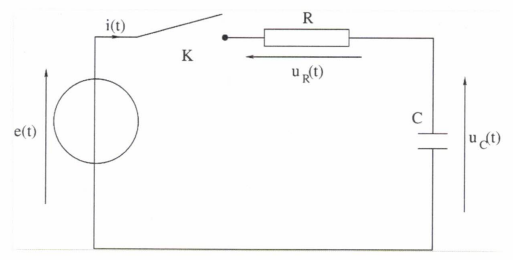
1.a.
Pout t < 0, que valent e(t), u c(t), i(t).
A t < 0, l'interrupteur est ouvert et le condensateur est déchargé :
e(t) = E ; u c(t) =0 ; i(t) = 0.
b. Etablir la
relation électrique entre e(t), u c(t) et i(t) lorsque K est
fermé.
Additivité des tensions: e(t) = u c(t) + u R(t).
uR(t).
= Ri(t) ; i(t) = dq(t) / dt = C duc(t) /dt.
E = RC duc(t) /dt + uc(t).
2.a. Montrer que
l'équation différentielle qui régit l'évolution de la tension u c(t)
peut s'écrire :
duc(t) /dt + uc(t)
/ t = E / t.
E = RC duc(t) /dt + uc(t).
duc(t) /dt + uc(t) / (RC) = E
/(RC).
On pose t = RC.
Par suite : duc(t) /dt + uc(t) / t = E / t.
b. c. Calculer la
constante de temps t.
RC = 104 x 10-6 = 10-2 s.
3.a Montrer que la résolution de
l'équation différentielle conduit à uc(t) = A+B exp(-t / t) avec A et B deux
constantes.
Solution générale de l'équation sans second membre : uc(t) = B exp(-t / t).
Solution particulière de l'équation avec second membre : uc(t)
= E ( condensateur chargé ).
Solution générale : uc(t) = B exp(-t / t) + E.
b. En déduire l'expression de uc(t)
en fonction de E et t.
A t=0; uc(0) = 0, condensateur déchargé.
o = B +E ; B = -E.
Par suite : uc(t)
= E(1- exp(-t / t)
).
c. Attribuer les
chronogrammes a, b et c aux signaux e(t), uc(t) et i(t).
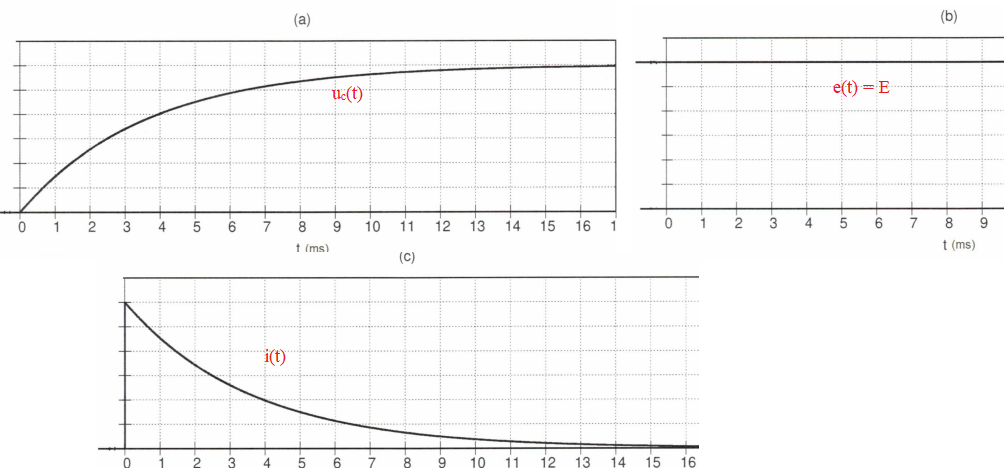
|
...
|
....
|
Le microscope (4,5 points).
1. L'objectif est une lentille mince notée L1 de vergence +100 dioptries.
a. Préciser la qualité convergente ou divergente de cette lentille.
La vergence étant positive, la lentille est convergente.
b. Donner la valeur de la distance focale objet.
Distance focale image : 1 /100 = 0,01 m = 1 cm.
Distance focale objet : -1 cm.
c. Si un objet AB
se trouve à l'infini par rapport à cette lentille, comment ressortent
les rayons issus de B à la traversée de la lentille.
L'image de cet objet se trouve dans le plan focal image de la lentille.
Les rayons issus de B à la traversée de la lentille, convergent en un
point du plan focal image.
2. En vous aidant de la figure ci-dessous, construire l'image A'B'. O1 est l'origine de l'axe.
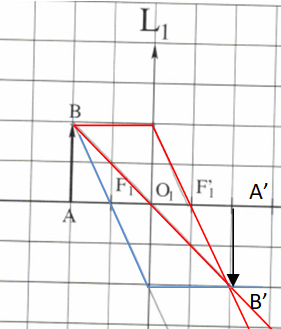
a. Donner la position sur l'axe optique de l'image A'B'.
O1A' = 2 cm.
b. Calculer le grandissement de l'image et qualifier cette image.
Grandissement = -1.
L'image est réelle, inversée par rapport à l'objet.
3. On place après L1 une seconde lentille L2, oculaire du microscope.
a. Comment A'B' doit être positionné par rapport à L2 pour que son image A"B" soit rejetée à l'infini ?
A'B' doit se trouver dans le plan focal objet de L2.
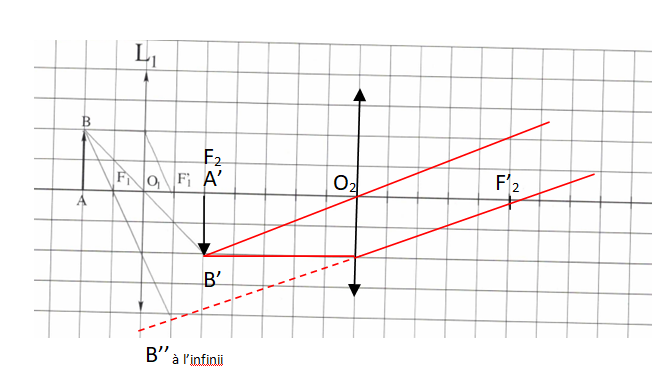
b. Indiquer la position des points remarquables ( F2 / F'2 foyer objet / image, O2 le centre optique ) de la lentille L2 de distance focale 5 cm.
O1F2 = 2 cm.
O1O2 = O1F2 + F2O2 = 2 +5 = 7 cm.
O1F'2 = 7 + 5 = 12 cm.
QCM 5 points.
QCM 1. A propos des lois de Kepler.
A. Les orbites des satellites sont des ellipses dont le centre de l'astre attracteur occupe le centre de l'ellipse. Faux.
Les orbites des satellites sont des ellipses dont le centre de l'astre attracteur occupe l'un des foyers de l'ellipse.
B. Le segment du centre de l'astre attracteur à un de ses satellites balaie des aires égales durant des durées égales. Vrai.
C. Le mouvement d'un satellite sur son orbite est un mouvement uniforme. Faux.
D. Soit T la période de rotation d'un satellite et a le demi-grand axe de son orbite, le rapport T2 / a3 est constant indépendant de la masse de l'astre attacteur. Faux.
T2 / a3 = 4 p2 / (GMastre)
E. Plus un satellite est éloigné de l'astre attracteur, plus sa vitesse de parcours sur son orbite diminue. Vrai.
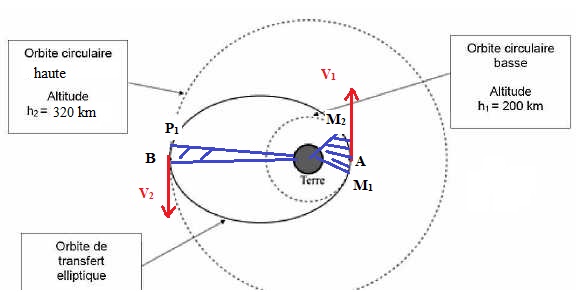
La distance M1 M2 est
inférieure à la distance P1 B.
Les durées de parcours entre les
points M1 et M2 puis P1 et B sont égales.
Donc la vitesse moyenne entre les points M1 et
M2 est supérieure
à celle entre les points P1 et B.
QCM 2
Un point matériel de masse m a une trajectoire circulaire de rayon R
constant. On note v la vitesse du point matériel. On donne trois
situations physiques, notées a, b et c.
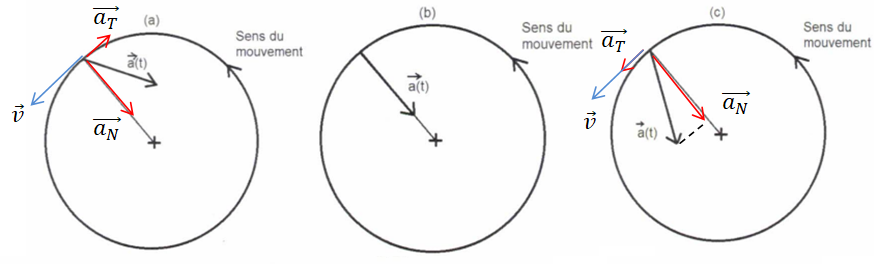
A. Dans le repère de Frenet, le vecteur accélération s'écrit :

B. Dans ce mouvement, il est possible d'obtenir un vecteur accélération nul. Faux.
Dans cette hypothèse v doit être nulle ainsi que dv /dt. Or la trajectoire est un cercle, donc v n'est pas nulle.
C. Un mouvement circulaire uniforme correspond à la situation physique a. Faux.
D. Un mouvement circulaire uniforme correspond à la situation physique b. Vrai.
E. Un mouvement circulaire ralenti correspond à la situation physique c. Faux. ( c'est a).
QCM 3.
Soit une porte d'entrée qui présente une atténuation accoustique par absorption de 20 dB.
Dans la rue un parteau-piqueur rentre en action avec une intensité sonore de valeur 10-2 W m-2 au niveau de la porte d'entrée.
A. Le niveau sonore du marteau piqueur dans la rue vaut 10 dB. Faux.
L = 10 log ( 10-2 / 10-12) =100 dB.
B. Le niveau sonore du marteau piqueur dans la rue vaut 100 dB. Vrai.
C. Le niveau sonore de l'autre côté de la porte vaut 10 dB. Faux.
100 - 20 = 80 dB.
D. L'intensité sonore derrière la porte vaut 10-4 W m-2. Vrai.
I = 10-12 x 108 = 10-4 W m-2.
E. Si l'intensité sonore du marteau-piqueur dans la rue est divisée par deux, son niveau sonore est divisée par deux aussi. Faux.
Le niveau sonore diminue de 10 log 2 = 3 dB.
QCM 4.
Soit le dispositif d'interférences dit des trous de Young notés S1, S2, espacés entre eux d'une distance a =1 mm et éclairés par un laser de longueur d'onde l = 600 nm. On récupère les franges d'interférences sur un écran à la distance D = 2 m des trous.
A. Pour une différence de marche d = -1,8 µm, on a une interférennce constructive. Vrai.
600 nm = 0,6 µm.
La différence de marche est égale à un nombre entier de longueur d'onde : interférences constructives.
B. Pour une différence de marche d = -1,8 µm, on a une interférennce destructive. Faux.
C. Pour une différence de marche d = 3,3 µm, on a une interférennce destructive. Vrai.
3,3 = 5,5 x 0,6.
La différence de marche est égale à un nombre impair de demi-longueur d'onde : interférences desstructives.
D. Tout point M de l'écran situé sur la médiatrice de [S1S2] donne un interférence constructive. Vrai.
E. Tout point M de l'écran situé sur la médiatrice de [S1S2] donne un interférence destructive. Faux.
|
|