Mathématiques,
Concours TSEEAC 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Partie 1.
On considère la suite (un) définie pour tout entier naturel n > 1 par : un = 1 +1 /2 +1 /3 +... 1/n.
Q1. Une fonction L écrite en langage Python qui a pour paramètre un nombre entier n > 2 et qui renvoie le n-ième terme de la suite est :
A. def L(n) :
u = 1
for i in range (2,n) :
u = u+1/i
return u. |
B. def L(n) :
u = 1
for i in range (1,n) :
u = u+1/ n
return u. |
C. def L(n) :
u = 1
for i in range (2,n+1) :
u = u+1/i
return u.
Vrai
|
D. def L(n) :
u = 1
for i in range (2,n) :
u = u+1/n
return u. |
La réponse A ne renvoie pas jusqu'au terme 1 / n+1.
Q2. La suite (un) vérifie :
A. Pour tout entier naturel n > 1, u2n-un > 0,5. Vrai.
Pour n = 2 : u2 = 1+1/2 ; u4 = 1+1/2 +1/3 +1/4 ; u4-u2 =1/3 +1/4 > 0,5.
U2n = 1 +1 /2 +...+1 / n +1 /(n+1) +...+1 /(2n) ; Un = 1 +1 /2 +...+1 /(n) ;
u2n-un =1 /(n+1) +...+1 /(2n), u2n-un > 0,5.
B. Pour tout entier naturel n > 1, u2n-un < 0,5.
C. Pour tout entier naturel n > 1, U 2n > 1+n/2. Vrai.
Par récurrence :
Initialisation : pour n = 1 ; u2 = 1 + 1/2 > 1+n/2 ; la propriété est vraie au rang 1.
Hérédité : U 2n > 1+n/2 est supposée vraie.
U 2n+1 = U 2 *2n ; U 2 *2n -U 2n > 0,5.
U 2n+1 > 0,5 +U 2n .
U 2n+1 > 0,5 +1+n/2 ; U 2n+1 > 1 /2 +1+n/2 ; U 2n+1 > 1+(n+1)/2 ;
Conclusion : la propriété est vraie au rang 1 et héréditaire, elle est vraie pour tout n entier naturel.
D. Pour tout entier naturel n > 1, U 2n < 1+n/2.
Q3. La suite (un) :
A. Converge car elle est croissante et majorée.
B. Converge car elle est décroissante et minorée.
C. Diverge car elle est minorée par une suite divergente non bornée. Vrai.
D'après la réponse Q2. C.
D. Diverge car elle est majorée par une suite divergente non bornée.
Partie II.
Soit la fonction f définie sur [0 ; +oo[ par f(x) = 10 exp(u(x)) avec u(x) = -exp(-2-0,1x).
Q4. Pour tout réel x > 0, la fonction est dérivable et :
A. f '(x) = exp(-e-2-0,1x).
B. f '(x) = (-20-x)exp(-e-2-0,1x).
C. f '(x) = 10 u(x) exp(u(x)).
D. f '(x) = - u(x) exp(u(x)). Vrai.
u'(x) = 0,1 exp(-2-0,1x)= -0,1 u(x).
f '(x) = 10 u'(x) exp(u(x)).
Q5. On admet que f '(x) est dérivable sur [0 ; +oo[ et on note f '' la dérivée de f '.
A. f ''(x) = 10(1+u(x)) u'(x) eu(x).
B. f ''(x) = 0,1(1+u(x)) u(x) eu(x). Vrai.
C. f ''(x) = -0,1 exp(-e-2-0,1x).
D. f ''(x) = (0,1x2+4x+39) exp(-e-2-0,1x).
On pose v = u'(x) =0,1 exp(-2-0,1x) = -0,1 u(x) et w =exp(u(x)).
v'= -0,01 exp(-2-0,1x) =0,01u(x).
w' =u'(x) exp(u(x))= -0,1u(x)exp(u(x)).
v'w+w'v = 0,01 u(x)exp(u(x))+u'2(x) exp(u(x))=0,01(u(x)+u2(x)) exp(u(x))=0,01 u(x)(1+u(x))exp(u(x)).
f "(x) = 10v'w+w'v =0,1 u(x)(1+u(x))exp(u(x)).
Q6. La fonction dérivée f ' est maximale pour :
A x=20 vrai ; B x=0 ; C. x = 10(2+0,1½) ; D.10(2-0,1½).
f ''(x) = 0,1(1+u(x)) u(x) eu(x).
0,1 eu(x) > 0 ; -u(x) > 0 ; f "(x) a le signe de -(1+u(x)) = - (1-exp(-2-0,1x))= exp(-2-0,1x)) -1.
f "(x) > 0 si exp(-2-0,1x) > 1 soit -2-0,1 x >0 ; 20+x < 0 ; x < -20. f '(x) est croissante.
f "(x) < 0 si x > -20. f '(x) est décroissante.
f "(x) =0 si x = -20. f '(x) est maximale.
Toutes les propositions sont fausses. Répondre E.
Partie III.
Q7. Le système suivant admet pour ensemble de solutions sachant que x et y appartiennent à [-p ; +p].
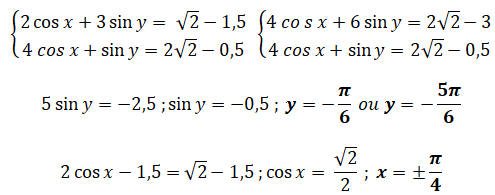
Réponse D.
Q8. Le système suivant admet pour ensemble de solutions sachant que x appartient à [-p ; +p].
Toutes les propositions sont fausses. Répondre E.
|
...
|
....
|
Partie IV.
On lance deux dés parfaitement équilibrés à 4 faces numérotées 1 ; 2 ; 3 ; 6. On considère la variable aléatoire X = cos(p /A)+ sin (p / B) où a correspond à la face obtenue par le premier dé et B par le second.
Q 9.
La probabilité p1 que X soit un entier est :
A. p1 = 0,25 ; B. p1 = 3 / 8 ; C. p1 = 5 / 16 vrai ; D. p1 = 9 / 16 .
Couples répondant à la problématique : ( 1 ; 1) ; (1 ; 2) ; (2 ; 1) ; (2 ; 2) ; (3 ; 6) sur 16 couples possibles..
Q10 La probabilité p2 que X soit un entier sachant que A est pair est :
A. p2 = 0,25 vrai ; B. p2 = 3 / 8 ; C. p1 = 5 / 16 vrai ; D. p1 = 9 / 16.
Couples répondant à la problématique : (2 ; 1) ; (2 ; 2) sur 8 couples possibles.
Q11 La probabilité p3 que X soit un nombre rationnel est :
A. p3 = 0,25 ; vrai B. p3 = 3 / 8 ; C. p3 = 5 / 16 vrai ; D. p3 = 9 / 16.
X ne doit pas être un entier, les couples ( 1 ; 1) ; (1 ; 2) ; (2 ; 1) ; (2 ; 2) ; (3 ; 6) ne conviennent pas.
X ne doit pas être un nombre irrationnel, donc A diffère de 6 et B diffère de 3.
Couples répondant à la problématique : (1 ; 6) ; (2 ; 6) ; (3 ; 1 ); (3 ; 2).
|
A=1
|
A=2
|
A=3
|
A=6
|
B=1
|
X= -1
|
X= -1
|
X = -1 /2
|
X = 1,866...
|
B=2
|
X=0
|
X=1
|
X = 3 / 2
|
X =0,866...
|
B=3
|
X = -1 +0,8666
|
X =0,866...
|
X =0,5 +0,866...
|
X = 0,866 +0,866...
|
B=6
|
X = -1/2
|
X =1 /2
|
X=1
|
X = 0,5 +0,866...
|
Partie V. -Dans un repère orthonormé de l'espace on considère les vecteurs suivants.
Q 12. Ces vecteurs sont :
A. non coplanaires ; B. coplanaires vrai ; C. colinéaires ; D. orthogonaux.
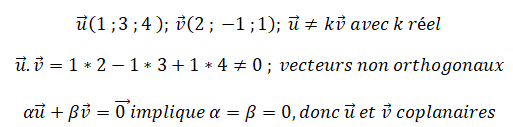
Q13 - le vecteur n de coordonnées (a ; b; c) est orthogonal aux vecteurs u et v si et seulement si :
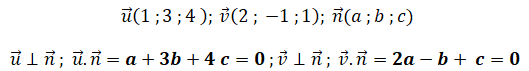
Réponse A.
Q14 - Ainsi, on montre que les coordonnées du vecteur n sont :
a+3b+4c=0 ; a = -3b-4c.
2(-3b-4c) -b+c = 0 ; -7b-7c=0 soit b = -c.
Par suite a = - c.
Coordonnées de ce vecteur n : k (-1 ; -1 ; 1) avec k réel.
Réponse C.
Q15 Une équation du plan passant par A(1 ; 1 ; 1) et de vecteurs directeurs u et v est :
A. -7x+5y+9z-7=0 ; B. x+y-z-1=0 vrai ; C. 9x-y+7z-15=0 ; D. -x-2y+2z+2=0 vrai.
Soit M(x ; y ; z) appartenant au plan.
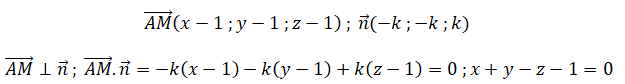
|
|