Mathématiques,
concours avenir 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Une
seule réponse exacte par question. Chque réponse exacte est gratifiée
de 3 points ; chaque réponse fausse est pénalisée par le retrait d'un
point.
Durée : 1 h 30 ; coefficient 6.
Géométrie du plan et de l'espace.
1. Soient P ,R et T trois plans de l’espace, deux à deux non parallèles. On appelle D la droite d’intersection du plan P avec
le plan R.
On peut alors affirmer que la droite D est :
a. forcément sécante au plan T
b. forcément parallèle au plan T
c. forcément incluse dans T
d. éventuellement parallèle au plan T. Vrai.
Soit P le plan d'équation cartésienne x = 0 et R le plan d'équation cartésienne y =0.
L'équation paramétrique de la droite D d'intersection est : x =0 ; y = 0 ; z = t avec t réel.

2. Dans le plan muni d’un repère orthonormé, on considère les points A(1 ;−1), B(4 ;−4) et C(2021 ;−2021).
Combien existe-t-il de cercle(s) passant(s) par ces trois points?
a. Aucun. Vrai.
b. Un unique
c. Deux exactement
d. Une infinité.
3. Dans le plan muni d’un repère orthonormé, l’ensemble des points M(x ; y) tels que x2+ y2-2x +4y −11 = 0 est un cercle
de centre le point de coordonnées :
a. (1 ;−2) vrai.
b. (−1 ;2)
c. (−2 ;1)
d. (2 ;−1).
x2-2x +1-1+ y2+4y +4-4−11 = 0.
(x-1)2 +(y+2)2 =16, cercle de centre (1 ; -2) de rayon 4.
4. Dans le plan muni d’un repère orthonormé, l’ensemble des points M(x ; y) tels que x4- y4= 0 est constitué :
a. d’une droite et d’un cercle
b. de deux droites et d’un cercle
c. de deux droites vrai
d. de deux droites et d’un point n’appartenant pas à celles-ci.
x4- y4=(x2+y2)(x2-y2)=(x2+y2)(x+y)(x-y)=0
x2+y2 =0, correspond à l'origine.
x+y = 0 correspond à la droite d'équation y = -x.
x-y = 0 correspond à la droite d'équation y = x.
5. Soient A et B deux points distincts du plan muni d’un repère orthonormé.
L’ensemble des points M tels que AM2− AB2= 0 est :
a. la médiatrice du segment [AB]
b. le cercle de centre A et de rayon AB vrai.
c. le cercle de centre B et de rayon AB
d. le cercle de centre B et de rayon racine carrée de AB.
AM2= AB2 soit AM = AB.
M appartient au cercle de centre A et de rayon AB.
6. Dans l’espace muni d’un repère orthonormé, on considère la droite D dont une équation paramétrique est donnée par :
x = 2t −1 ; y = −4+2t ; z = 1+t avec t réel.
La droite D coupe le plan de base xOz au point de coordonnées :
a. (3 ;0 ;3) vrai
b. (−3 ;−6 ;0)
c. (0 ; -3 ; 1,5)
d. (0 ;2 ;0).
Equation cartésienne du plan xOz : y =0. Les réponses b, c et d sont donc exclues.
A(3 ; 0 ; 3) appartient-il à D ?
3=2t-1 soit t = 2 ; y = -4+2*2 =0 est vérifié ; 3 = 1+2 est vérifié.
A(3 ; 0 ; 3) appartientbien à D.
7. Dans le plan muni d’un repère orthonormé, on considère le cercle C d’équation cartésienne x2+ y2−6x +3 = 0 et D la droite d’équation réduite y = ax.
A quel intervalle doit appartenir le nombre réel a pour que D et C aient au moins un point en commun ?
a .[-3½ ; 3½] ; b. [0 ; 3½] ; c. [0 ; 2½] ; d. [-2½ ; 2½].Vrai.
x2+ a2x2−6x +3 = 0 ; (1+a2)x2−6x +3 = 0.
Discriminant D :(-6)2-4*3(1+a2) > 0.
36-12-12a2> 0 ; 2-a2> 0. a2 < 2.
Calculs numériques, suites numériques.
8. Combien existe-t-il de nombre(s) réel(s) égaux à leurs inverses ?
a. Aucun
b. Un unique
c. Exactement deux vrai
d. Une infinité.
x = 1 /x ; x2 = 1 ; x = ±1.
9. Quels que soient les réels a, b et c, on a : (a +b)2−(a +c)2=
a. (b −c)(2a +b +c) vrai
b. (b −c)(a +2b +c)
c. (b −c)(a +b +2c)
d. (a −c)(a +2b +c).
(a +b)2−(a +c)2=[(a+b)+(a+c)][(a+b)-(a+c)]=(2a+b+c)(b-c).
10. Soient a =(3+2*3½) / 7½ et b = 7½.
On peut alors affirmer que :
a. a < b vrai
b. a > b
c. a = b
d. les nombres a et b ne peuvent pas être comparés.
a-b =(3+2*3½) / 7½ -7 / 7½ =(3+2*3½-7) /7½ =(-4 +2*3½) / 7½ < 0.
11.Pour n ∈N∗, on peut affirmer que la somme des n premiers entiers pairs non nuls 2+4+···+2n est égale à :
a. n(n +1)/2 ; b. 2n(n +1) /2 vrai ; c. n(2n +1) /2 ; d. 2n(2n +1) /2.
Somme des termes d'une suite arithmétique de premier terme u1=2 et de raison 2.
n (u1 + un) / 2 =n( 2+2n) / 2.
Pour les deux questions suivantes, on considère les suites (un) et (vn) définies par :
u0 = 1; un+1 = (−1)n −un pour tout n ∈N
et vn = (−1)nun pour tout n ∈ N.
12.
La suite (vn) est :
a. arithmétique de raison −1 vrai
b. géométrique de raison 1
c. géométrique de raison −1
d. ni arithmétique, ni géométrique.
vn+1 = (−1)n+1un+1 = (−1)n+1( (−1)n −un )=(-1)2n+1- (−1)n+1un= -1+(−1)nun= -1 +vn.
13. Pour tout entier naturel n, on a :
a. un = n(−1)n +n
b. un = n(−1)n +n(−1)n
c. un = (−1)n −n(−1)n. Vrai.
d. un = 1−n2.
vn =v0+n(-1)=v0-n=1-n. ( suite arithmétique de raison -1 et de premier terme v0 = 1)
un=vn /(-1)n =(-1)n (1-n)= -1n -(-1)n n.
14. Soient (un) et (vn) des suites adjacentes, qui convergent vers le réel ℓ différent de 0. Les suites (an) et (bn), définies par
an = un −ℓ et bn = vn −ℓ sont :
a. adjacentes et convergent vers 0. Vrai.
b. adjacentes et convergent vers ℓ
c. adjacentes et convergent vers −ℓ
d. non adjacentes.
En plus l'infini : limite de ( un −ℓ )= limite de un −ℓ =0.
limite de ( vn −ℓ )= limite de vn −ℓ =0.
Elle sont adjacentes : en plus l'infini, limite de an-bn = 0.
15.
Soit (un) une suite monotone. Les suites (un) et (−un) :
a. sont forcément adjacentes
b. ne peuvent pas être adjacentes
c. sont adjacentes uniquement si (un) converge
d. sont adjacentes uniquement si (un) converge vers 0. Vrai.
un -(-un)=2un. Donc les suites (un) et (−un) sont adjacentes.
En plus l'infini, la limite de 2 un est nulle.
16.Deux suites constantes sont adjacentes si et seulement si elles sont :
a. nulles
b. convergentes
c. égales vrai
d. convergentes vers 0.
un = a ; vn = b ; limite en plus l'infini de (un-vn) : a-b= 0 soit a = b.
17.Soient (un) et (vn) des suites adjacentes, avec (un) croissante et (vn) décroissante.
Soit (wn) une suite croissante qui converge vers un réel ℓ.
On peut alors affirmer que les suites (un +wn) et (vn −wn) :
a. sont forcément adjacentes
b. ne peuvent pas être adjacentes
c. sont adjacentes uniquement si ℓ = 0 vrai
d. aucune de ces réponses n’est correcte.
un+wn-(vn-wn)=un-vn+2wn.
Or la limite en plus l'infini de un-vnest égale à zéro.
La limite en plus l'infini de un+wn-(vn-wn) est égale à 2 ℓ.
18. Soient (un) et (vn) deux suites non nulles, respectivement arithmétique de raison r et géométrique de raison q.
Sachant que la suite (un ×vn) est géométrique, on peut affirmer que :
a. r = 0 et q = 1 ; b. r = 0 vrai ; c. q = 1 ; d. r = 0 ou q = 1.
un = u0+nr ; vn =v0 qn ; un ×vn=v0 qn (u0+nr) =v0u0 qn +n r v0 qn.
v0, u0 et q ne sont pas nulle, donc si r = 0, la suite (un ×vn) est géométrique.
Fonctions.
19. Soit n entier non nul, la fonction définie sur R par : f(x) = 1+x+x2+...+xn.
On note C sa courbe représentative. L'équation de la tangente à C au point d'abscisse 1 admet pour équation :
f '(1) = 1 +2+...+n =n(n+1) /2 ( somme des termes d'une suite arithmétique de raison1 et de premier terme 1).
f(1) =1+1+12+...+1n=n+1.
Equation de la tangente : y = f '(1) x+b = n(n+1) / 2 x +b.
Le point de coordonnées (1 ; f(1)) appartient à la tangente :
f(1)=n+1 =n(n+1) / 2+b ; b =(n+1) (1-n/2).
y = n(n+1) / 2 x +(n+1) (1-n/2)= n(n+1) / 2 x +(n+2-n2)/2. Réponse B.
20. On donne la courbe représentative d'une fonction f, définie et dérivable sur [1 ; 13].
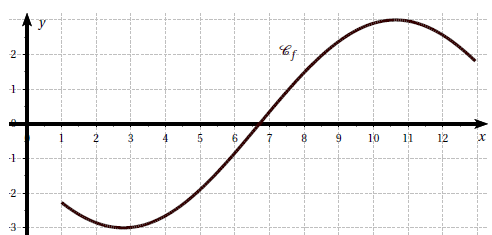
Combien l’équation f ′(x) = 0 possède-t-elle de solution(s) dans l’intervalle [1;13]?
a. 0 ; b. 1; c. 2 vrai ; d. 3.
La dérivée s'annule quand la courbe présente un extrémum ( tangente horizontale ).
21.On admet que, pour tout nombre réel x, on a : ex> x +1.
On peut alors affirmer que pour tout nombre réel x, on a :
a. exp(−x2) < (x −1)(x +1)
b. exp(−x2) < -x2+1.
c. exp(−x2) > x2-1.
d. exp(−x2) >(1-x)(1+x). Vrai.
On remplace x par -x2 dans ex> x +1 : exp(−x2) > -x2+1=1-x2.
exp(−x2) > (1-x)(1+x).
22. Pour tout réel x, on a : ln[(1+ex) / (1+e-x)] =
a. ex ; b. e2x ; c. x vrai ; d. 2x.
ln[(1+ex) / (1+e-x)] =ln[ex(1+e-x) / (e-x(1+ex)] =ln(ex-(-x) )+ln[(1+e-x) /(1+ex)]=ln(e2x)-ln[(1+ex) /(1+e-x)].
2ln[(1+ex) / (1+e-x)] =ln(e2x) = 2x.
ln[(1+ex) / (1+e-x)] = x.
23.
Soit f la fonction définie et dérivable sur R par : f (x) = exp(xex)
On a alors f ′(x) =
a. exp(xex) ; b. (x +1)exp(xex) ; c.(x+1) exp((x+1)ex) vrai ; d. (x+1) exp(x(1+ex)).
On pose w =xex ; u = x et v = ex ; u' = 1 ; v' = ex.
w' = u'v +v'u = ex+xex=(x+1)ex.
f '(x) = w' w =(x+1)ex exp(xex) =(x+1) exp(ex(x+1)).
24. Sachant que a > 0 et que la fonction f , définie et dérivable sur R par f (x) = ln(eax +e-ax) est telle que la limite en plus l'infini de f '(x) = 8 on peut affirmer que :
a. a = 1 ; b. a = 2 ; c. a = 4 ; d. a = 8. Vrai.
On pose u = eax +e-ax ; u' = aeax -ae-ax ; f '(x) = u' / u = a(eax -e-ax ) / (eax +e-ax).
f '(x) =aeax (1-e-2ax ) / [eax (1-e-2ax )]=a(1-e2ax ) / (1-e-2ax ).
En plus l'infini, e-ax tend vers zéro car a > 0 et f '(x) tend vers a.
25. Le domaine de définition de la fonction f définie par f (x) = ln(x2) est égal à :
a. R∗ vrai ; b. R ; c. ]0 ;+∞[ ; d. [0 ;+∞[.
x2 doit être différent de 0.
26. Soit f une fonction définie et deux fois dérivable sur R et telle que f ′(0) = 0.
Sachant que f est concave, on peut affirmer que f est :
a. à valeurs positives ou nulles sur [0 ;+∞[
b. à valeurs négatives ou nulles sur [0 ;+∞[
c. croissante sur [0 ;+∞[
d. décroissante sur [0 ;+∞[. Vrai.
f est concave : f " < 0 et f ' est décroissante.
Or f '(0) =0 : f ' > 0 sur ]-oo ; 0] et f '(x) < 0 sur [0 ; +oo[.
f est croissante sur ]-oo ; 0] et décroissante sur [0 ; +oo[.
27. Quel est l’antécédent par la fonction exponentielle de l’antécédent par la fonction logarithme népérien de 0 ?
a. 0 vrai ; b. 1 ; c. e ; d. Celui-ci n’existe pas parce que la fonction ln n’est pas définie en 0.
ln(1) =0 ; ex = 1 soit x = 0.
|
...
|
....
|
28. La somme S est égale à :
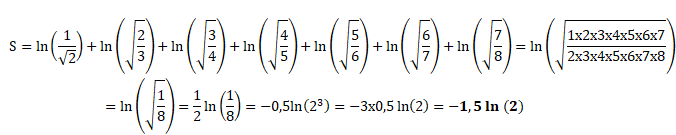
Réponse C.
29.
Soit sh la fonction définie sur R par sh(x) =(ex −e−x)/2 et α une solution de l’équation ln(ex −e−x)=1. On peut alors affirmer
que :
a. ln(sh(α)) < 0
b. ln(sh(α)) > 0 vrai
c. ln(sh(α)) = 0
d. Aucune de ces réponses n’est correcte.
ln(eα −e−α)= ln(2sh(α))=1 ; ln(2) + ln(sh(α)) = 1 ; ln(sh(α)) = 1-ln(2) > 0.
30. Soit f la fonction définie sur R par : f (x) = xe2x.
L’équation de la tangente à la courbe représentative de f dans le plan
muni d’un repère orthonormé en son point d’inflexion a pour équation :
a. y = −e−2x −2e−2 vrai
b. y = −3e−4x −8e−4
c. y = 3e2x −2e2
d. y = 5e4x −8e2.
f '(x) =e2x+2xe2x ; f "(x)=2e2x+2e2x+4xe2x =4e2x(1+x).
f " s'annule et change de signe pour x = -1 ( point d'inflexion).
f '(-1) =e-2(1-2= -e-2.
Equation de la tangente : y = -e-2x +b.
Le point (-1 ; f(-1)=-e-2) appartient à la tangente.
-e-2=e-2 +b ; b = -2e-2 ; y = -e-2x -2e-2.
31.
La fonction f , définie sur ]0 ;+∞[, par : f (x) = x2 (2ln(x)−3) est :
a. concave sur ]0 ;1[, convexe sur ]1 ;+∞[ vrai
b. convexe sur ]0 ;1[, concave sur ]1 ;+∞[
c. concave sur ]0 ;e[, convexe sur ]e ;+∞[
d. convexe sur ]0 ;e[, concave sur ]e ;+∞[.
Calcul de f '(x) en posant u = x2 et v = 2ln(x)−3 ; u' = 2x ; v' = 2 /x.
f '(x) = 2x(2ln(x)−3) +2x = 2x(2ln(x)−2)
Calcul de f "(x) en posant u = 2x et v = 2ln(x)−2 ; u' = 2 ; v' = 2 /x.
f "(x)=2(2ln(x)-2)+4 =4 ln(x).
f " s'annule pour x = 1.
f " est négative sur ]0 ; 1[, f(x) est concave.
f " est positive sur ]1 ; +oo[, f(x) est convexe.
32. La limite en plus l'infini de (4x+1)½-x½) / x½ est égale à :
a. 0 ; b. 1 vrai ; c. −∞ ; d. +∞.
[(4x+1) / x]½-1 = [ 4+1 /x]½-1
En plus l'infini : 1 /x½ tend vers zéro ; 4½-1 tend vers 1.
33.
Soient u et v deux fonctions définies sur R telles que :
La limite en plus l'infini de u(x) est égale à moins l'infini.
La limite en plus l'infini de v(x) est égale à plus l'infini.
Sachant de plus que v est impaire, on peut affirmer que la fonction f = v ◦u, définie sur R par f (x) = v (u(x)) est telle que :
la limite en plus l'infini de f(x) est égale à :
a. 0 ; b. +∞ ; c. −∞ vrai
d. Aucune de ces réponses n’est correcte.
En plus l'infini, la limite de u(x) est égale à moins l'infini.
La
limite en plus l'infini de f(x) est égale à la limite en moins l'infini
de v(X) soit moins l'infini car v est impaire et que la limite en plus l'infini de v(x) est égale à plus l'infini.
Primitive et équation différentielle.
34. Soit f la fonction définie sur R par f (x) =1/3e2x+5-2
La
primitive F de f sur R dont la représentation graphique coupe l’axe des
ordonnées au point d’ordonnée 3 a pour expression F(x) :
F (x) =1/6e2x+5-2x+Cste.
F(0) = 3 = 1/6e5 +Cste.
Cste = 3-1/6e5.
F(x) =1/6e2x+5-2x+3-1/6e5. Réponse B.
35. Soit f une fonction définie et dérivable sur R telle que f ′ = f et f
(0) = 2f ′(0).On peut alors affirmer que, pour tout réel x,
f (x) =
a. ex ; b. e2x ; c. e0,5x ; d. 0.Vrai.
Les solutions de l'équation différentielle f = f ' sont de la forme f = kex avec k une constante.
Il faut de plus f(0 = f '(0) soit k = 0.
36. Si f est solution sur
R de l’équation différentielle y′(x)+3y(x) = 0 (E), alors la fonction g
= 2f est solution sur R de l’équation
différentielle :
a. y′(x)+3y(x) = 0 vrai
b. 2y′(x)+3y(x) = 0
c. y′(x)+6y(x) = 0
d. Aucune de ces réponses n’est correcte.
g' = 2 f ' soit f ' = 0,5 g' ; repport dans (E) : 0,5 g'+1,5 g =0.
g' + 3g = 0.
37. Soit g une fonction définie et dérivable sur R, solution de l’équation différentielle y′(x)− y(x) = f (x), où f est elle-même
une fonction définie et dérivable sur R, solution de l’équation différentielle y′(x)+3y(x) = 0.
On peut alors affirmer que la fonction g ′ est solution sur R de l’équation différentielle :
a. y′(x)− y(x) = 0
b. y′(x)− y(x) = f (x)
c. y′(x)− y(x) = −3f (x) vrai.
d. y′(x)− y(x) = −2f (x).
g'-g=f ; g"-g' = f ' ;
f ' +3 f = 0 soit f ' = -3f ;
g"-g' = -3f ; (g') '-g ' =-3f.
Dénombrement et probabilités.
38. Sachant que (n 2)=15, on peut affirmer que n est :
a. impair ; b. multiple de 6 vrai ; c. un nombre premier ; d. multiple de 5.
(n 2)=n (n-1) / 2 =15 ; n(n-1)=30.
n2-n-30=0 ; discriminant D =1+4*30=121=112 ; solution positive : (1+11) / 2 = 6.
39. Soient A et B deux événements indépendants tels que P(B) =0,5P(non A) et P(A∪B) = 0,68. On a alors P(A) =
a. 0,6 vrai ; b. 0,06 ; c. 0,36 ; d. 0,46.
P(A∪B) =P(A) +P(B) - P(A ∩ B)
Les événements sont indépendants, donc P(A ∩ B)= P(A) * P(B).
P(A∪B) =P(A) +P(B) -P(A) * P(B).
P(A∪B) =P(A) +0,5 (1-P(A))-0,5P(A)(1-P(A)).
0,68 = P(A) +0,5 -0,5P(A)-0,5P(A)+0,5 P(A)2.
0,5 P(A)2=0,68-0,5 =0,18 ; P(A)2=0,36 ; P(A) = 0,6.
40.On lance huit fois une pièce de monnaie bien équilibrée. La probabilité d’obtenir exactement 7 "Pile" est égale à :
a.0,5 ; b. 0,53 ; c. 0,55vrai ; d. 0,58.
La variable aléatoire X compte le nombre de "pile" ; X suit une loi binomiale de paramètre n = 8 et p = 0,5.
P(X=7) = (87) 0,57*0,51 =8 *0,58 =23 *0,58 =1/0,53*0,58 =0,55.
41.
Soient n ∈N∗ et X et Y deux variables aléatoires telles que :
X suit la loi binomiale de paramètres n et 0,1;
Y suit la loi binomiale de paramètres n2 et 0,1.
Quelle est la valeur de n sachant que E(X +Y ) = 2?
a. 1 ; b. 2 ; c. 3 ; d. 4. Vrai.
E(X +Y ) =E(X)+E(Y)= 2.
n*0,1 + n2*0,1=2.
n2+n-20=0 ; discriminant D =1+80=81=92.
Solution positive retenue : (-1+9)/2=4.
42. Soient X1, X2,..., X5, cinq variables aléatoires telles que pour tout i entier tel que 1 < i < 5, la variable aléatoire Xi suit la
loi binomiale B(8 ; 0,5i).
On définit également la variable aléatoire M par :M = (X1+X2+X3+X4+X5) / 5.
On a alors : E(M) =
a. 21 /20 ; b. 21 /40 ; c. 31 /40 ; d. 31 /20. Vrai.
E(M) =(8 x0,5 +8 x0,52 +8 x0,53 +8 x0,54 +8 x0,55 ) / 5=0,8(1+0,5+0,25+0,125+0,0625)=0,8 x1,9375=1,55=31 /20.
43. Soit X une variable aléatoire suivant la loi binomialeB(n ;p) de paramètres n et p, avec p ∈]0 ;1[. On peut alors affirmer
que :
a. E(X) = pV (X) ; b. V (X) = pE(X) ; c. E(X) = (1−p)V (X) ; d. V (X) = (1−p)E(X). Vrai.
E(X) = n p ; V(X) = n p (1-p) =E(X) (1-p).
Algorithmique et programmation.
Pour les questions 44 à 45, on considère l’algorithme suivant :

44. Pour une valeur saisie de N par l’utilisateur, que retourne cet algorithme?
a. La somme des entiers de 1 à N
b. La somme des inverses des entiers de 1 à N vrai
c. L’inverse de la somme des entiers de 1 à N
d. L’inverse de la somme des inverses des entiers de 1 à N.
45. Pour une valeur saisie de N égale à 5, l’algorithme retourne une valeur comprise entre :
a. 0 et 1 ; b. 1 et 2 ; c. 2 et 3 vrai ; d. 3 et 4.
0+1+1/2+1/3+1/4 +1/5 ~2,28.
|
|
|
|