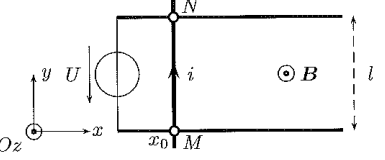
Rails de Laplace,  concours ENAC pilote 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... On considère des rails de Laplace, conducteurs et de résistance négligeable, distants de l, disposés selon un plan horizontal. Une barre rigide MN conductrice, de résistance R=10 kW et de masse linéique rl , est assujettie à rester perpendiculaire aux deux rails. Elle peut se déplacer sans frottement, selon un mouvement de translation rectiligne, le long des rails. L’ensemble est plongé dans un champ magnétique B externe uniforme et vertical. À l’instant initial, on branche, entre les deux extrémités des deux rails, un générateur idéal qui impose une tension constante U. On notera 𝑖 l’intensité (éventuellement variable) du courant électrique qui circule dans le circuit. On note x0 la position initiale de la barre.   25. Parmi les définitions suivantes, quelles sont celles dont le contenu est incomplet ?  A) La force de Lorentz est la force qui s’exerce sur une charge d, de vitesse v dans le référentiel d’étude. Incomplet.  B) La force de Laplace est la force qui s’exerce sur un conducteur parcouru par un courant d’intensité 𝑖. Incomplet. Le conducteur  ( ou la charge )doit se trouver dans un champ magnétique.  C) Un champ magnétique uniforme est un champ qui ne varie pas dans l’espace. D) Le flux d’un champ magnétique uniforme à travers une surface orthogonale au champ s’appuyant sur un contour orienté est égal, au signe près, au produit de la norme du vecteur champ magnétique par l’aire de la surface considérée. 26. En vous appuyant sur la figure ci-dessus, déterminer à tout instant, le vecteur force de Laplace.. 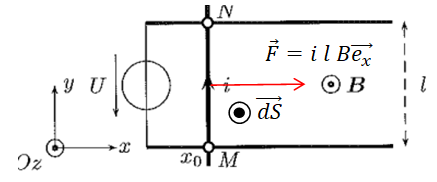Réponse A. 27.  Donner l’équation du mouvement de la barre. A) x"= -iB / rl .   . B) x" =-iB  rl . C) x" =-i l B. D) x"= iB / rl . Vrai. Le poids et l'action des rails se neutralisent. La seconde loi de Newton écrite sur l'axe horizontal donne :  mx" = i l B ; x" = i l B / m. rl= m /  l ; x"= iB / rl .   28.   Le déplacement de la tige provoqué par la force de Laplace génère un phénomène d’induction dans le circuit. Quelle est la force électromotrice ein correspondante ? A) ein = −l B x'. Vrai. ̇ B) ein = i B x'.̇ C) ein = −il B x'.̇ D) ein = i l B x'. Surface balayée par le barre se déplaçant à la vitesse x' duant dt : dS = l x' dt. Flux magnétique  dF = BS =Bl x' dt. fem induite : ein = -dF / dt = - B l x'. 29. Quelle relation entre x'̇, i et U peut-on déduire de la question qui précède ? A) B l x' +Ri = -U. B) B l x' -Ri =U. C) B l x' +Ri =U. Vrai. D) -B l x' +Ri =U. Le sens du courant induit est tel que par ces effets électromagnétiques il s'oppose au déplacement de la barre. La force de Laplace induite est colinéaire à la vitesse mais de sens contraire : d'où le sens du courant induit i ( opposé à i) U+ein = Ri. U -B l x = Ri. Bl x' +Ri =U. 30. Déduire de ce qui précède l’équation différentielle décrivant l’évolution de i dans le circuit, puis celle décrivant l’évolution de la vitesse v= x' de la barre. i = U / R -B l x' / R. On dérive : di /dt = 0 -B l x" / R. Or x"= iB / rl . di/dt +  B2 l / ( R rl )i = 0. x"= iB / rl ; i =U / R -B l x' / R. x" = U B / ( R rl ) - B2 l x' / ( R rl ). x"=dv /dt  ; x' = v. dv /dt +B2 l v / ( R rl ) = U B / ( R rl ). Réponse A.

menu