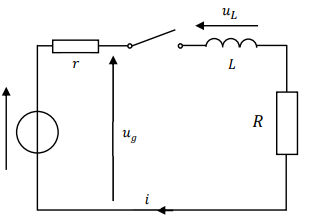
Circuit RL,  concours ENAC pilote 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Une bobine d’inductance 𝐿 (résistance négligeable) est placée en série avec un résistor de résistance 𝑅. L’ensemble est alimenté par un générateur de tension continue de force électromotrice 𝐸 et de résistance interne 𝑟. À l’instant 𝑡 = 0 initial (𝑡 désigne le temps), on ferme le circuit série à l’aide d’un interrupteur.   7.  Quel est l’ordre de grandeur de l’inductance 𝐿 des bobines couramment utilisées en travaux pratiques ?  A) Le mégahenry (MH) ; B) Le millihenry (mH) vrai ; C) Le nanohenry (nH) ; D) Le kilohenry (kH). 8. Déterminer l’équation différentielle du premier ordre vérifiée par l’intensité 𝑖(𝑡) qui circule dans la bobine. Additivité des tensions : ug =uR +uL ; ug = E-ri ; uL = Ldi/dt ; uR = Ri. E-ri = L di / dt +Ri. Ldi /dt +(R+r) i = E. On pose t= L / (R+r). di /dt + i / t = E / L. Réponse D. 9. Quelle est la solution de l’équation différentielle précédente ? Solution générale de l'équation sans second membre : i =A exp(-t / t) avec A une constante. Solution particulière de l'équation : i=E/(R+r). Solution générale de l'équation avec second membre : i= A exp(-t / t) +E / (R+r). i(t=0) = 0 ; A+E /(R+r) =0 ; A = -E/(R+r). i= E/ (R+r) [ 1-exp(-t / t)]. Réponse B. 10. Déterminer la tension 𝑢𝐿(𝑡) aux bornes de la bobine. di /dt = E / [ t (R+r)] exp(-t / t). di / dt = E / L exp(-t / t). uL(t) = Ldi/dt =E  exp(-t / t). Réponse B.   11. Comment évolue la tension 𝑢𝑔(𝑡) aux bornes du générateur ?  A) La tension aux bornes du générateur reste constante et égale à 𝐸.  B) La tension aux bornes du générateur devient nulle. C) La tension aux bornes du générateur évolue selon 𝑢𝑔(𝑡) = 𝐸 − 𝑟𝑖(𝑡). D) La tension aux bornes du générateur diminue et devient égale à RE / (r+r) au bout d’une durée suffisamment longue. ug(t) = E-r i = E-r E/ (R+r) [ 1-exp(-t / t)]. Au bout d'un temps assez long : exp(-t / t) tend vers zéro. ug(t) =E-r E/ (R+r)= [E(R+r)-rE ] / (R+r) =E R / (R+r).  Réponses C et D. 12. .On remplace maintenant le générateur de tension continue par un GBF qui délivre une tension sinusoïdale de pulsation w. Comment évolue la tension complexe uL , associée à uL , en fonction du courant complexe 𝑖 associé à 𝑖 ? i(t) = I exp(jwt + J). di(t) /dt = j I w exp(jwt + J). uL(t) = j L w I exp(jwt + J) = jLw i(t).  Réponses A et B.

menu