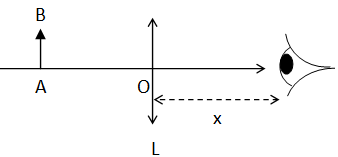
Une loupe, assimil�e � une lentille mince L de distance focale image f '
0
> 0 et de centre optique O, est utilis�e pour observer
un objet AB situ� dans un plan de front. L’ensemble est plac� dans
l’air dont on supposera l’indice de r�fraction �gal � l’unit�.
L’œil de l’observateur est situ� � une distance x > 0 en arri�re de
la lentille. On mod�lise cet œil, que l’on
suppose sans d�faut (œil emm�trope), comme l’association d’une lentille
mince L' de vergence variable et d’un capteur fixe
(la r�tine). On note la distance entre l’œil et son punctum proximum,
c’est-�-dire, la distance minimale de vision nette : d
m = 25 cm. Dans tout l’exercice, on admet que les conditions de Gauss sont satisfaites.
On d�finit le grossissement G de la loupe par le rapport
q ' /
q
de l’angle
q '
sous lequel l’objet est vu � travers L sur l’angle
q sous
lequel on voit l’objet directement (sans la loupe) lorsqu’il est plac� au punctum proximum. Dans cette d�finition, la valeur
de G d�pend de la position de l’objet et de la position de l’œil. On cherche les conditions d’observation qui maximisent le
grossissement.
On donne la relation de conjugaison de Descartes, celle de Newton et le grandissement transversal G
t
pour une lentille
mince de distance focale image f
i
:
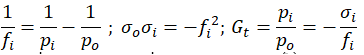
p
oet p
i
sont respectivement les distances alg�briques de l’objet et de son image au centre de la lentille.
En outre,
so et
si
sont les distances alg�briques respectives de l’objet au foyer principal objet et de l’image au foyer principal image.
7. Que peut-on affirmer ?
A) La limite de r�solution angulaire d’un œil normal est d’environ 1,5"
.
Limite de r�solution de l'oeil humain : 3 10
-4 rad =3 10
-4 x180 / 3,14 ~0,017 degr� soit 0,017 x3600 ~62 ".
B) Un ballon sph�rique de 20 cm de diam�tre plac� � une distance de 100 m est vu sous un angle sup�rieur � la
limite de r�solution angulaire d’un œil sans d�faut.
Vrai.
diam�tre apparent du ballon = 0,20 /100 =2 10
-3 rad > 3 10
-4 rad.
C) Un œil emm�trope peut observer nettement un objet � l’infini.
Vrai.
D) Un objet virtuel pour l’œil peut �tre observ� nettement.
Cet objet virtuel se situe derri�re le cristallin ; on ne peut pas le voir nettement.
8. Dans cette question, AB est plac� dans le plan focal objet de L et la position de l’œil, derri�re la lentille, est quelconque.
L’œil voit nettement l’image de AB � travers L. D�terminer
q'
et G.
A) q'= AB / d
m
;
B) q'= AB / f '
vrai ;
C) G = f ' / d
m ;
D) G =d
m / f '
vrai.
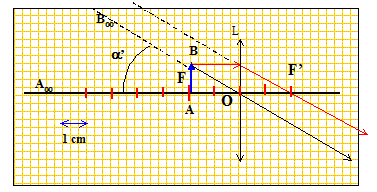
L'image A'B' donn�e par la loupe se trouve � l'infini, l'objet AB �tant dans le plan focal objet.
p
0 = -f
i ;
q'=
a'= AB / f '
;
q = AB / d
m ; G =
q' /
q =d
m / f '.
9. L’objet AB n’est plus dans le plan focal de L. L’œil est plac� � proximit� de la loupe (x ≈ 0) et accomode de sorte qu’il
observe l’image de l’objet � travers L � son punctum proximum. � quelle position p
1= mesure alg�brique de OA l’objet est-il plac� et que vaut
alors le grossissement G
de la loupe dans ces conditions d’observation ?
A) p
1 =d
m f ' / (d
m-f ').
B) p
1 = -d
m f ' / (d
m+f ')
vrai.
C) G
1 = d
m / f '.
D) G
1 =1 + d
m / f '
vrai.
p
i = -d
m.
1 / f ' = 1 / p
i -1 / p
1 = -1 / d
m -1 / p
1 ;
1 / p
1 = -1 / d
m -1 / f ' = - ( f ' +d
m) / ( f ' d
m) ; p
1 = -d
m f ' / (d
m+f ').
G = p
i / p
1 = (d
m+f ') / d
m = 1 + d
m / f '.
10. L’œil est d�sormais plac� � une position quelconque dans l’intervalle 0 < x ≤ d
m. On note A
oo la position de A qui permet
� l’œil d’observer l’image de l’objet donn�e par L sans accomodation et A
m la position de A qui oblige l’œil � accommoder
au punctum proximum. On introduit les distances alg�briques p
oo = mesure alg�brique de OA
oo et p
m = mesure alg�brique de OA
m.
Exprimer ces derni�res
A) poo = -f ' vrai ;
B) poo =x -f ;
C) pm = - f '(dm-x) / ( f ' +dm-x) vrai D) pm = f '(x-dm) / ( f ' -dm+x)
L'oeil n'accommode pas en observant l'image � l'infini ; l'objet est donc au foyer objet de la loupe : p
oo = - f '.
Si l'image se situe � d
m : p
i = x-d
m.
1 / f ' = 1 / p
i -1 / p
m =1 / (x-d
m) -1 / p
m = 1 / p
m =1 / (x-d
m) - 1 / f ' =(f '+d
m-x) / (f ' (x-d
m)).
p
m =(f ' (x-d
m)) / (f '+d
m-x).
11. On note p = mesure alg�brique de OA, la position de A telle que p
oo ≤ p ≤
pm. Calculer le grossissement G(x,p) de la loupe pour ces positions x de l’œil et p de l’objet.
A) f ' d
m / [(x-p)(f '+p)]
;
B) f ' dm / [(x-p)(f '-p)]
;
C) f ' d
m /(x f ' +px +p f ').
D) f ' d
m /(x f ' +px -p f ').
Vrai.
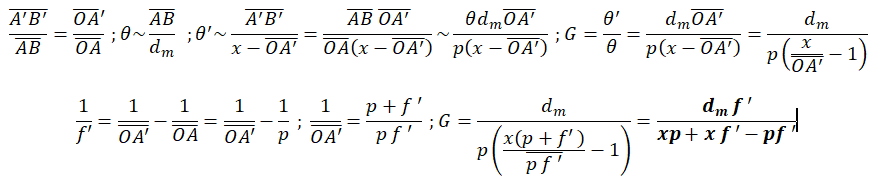12. On note A'
l’image de A par L et p' = mesure alg�brique de OA'. Pour quelle position x de l’œil et quelle valeur de p '
le grossissement est-il
maximum ?
A) x = d
m et p' = 0.
B) x = 0 et p' = -d
m.
Vrai C) x quelconque et p' = -oo.
D) x =0 et p' = -f '.
d
m et f ' sont des constantes.
Le grossissement est maximum si le d�nominateur xp+xf '-pf ' = x(p + f ') -p f 'est minimal.
p < 0 et p
< p
oo = - f ' alors p + f ' >0 ;
-p f ' >0 ; l'expression x(p + f ') -p f 'est minimal quand x =0. ( cas de la question 9).
p' = -d
m ;
q ' est d'autant plus grand quand l'image est plus proche.
