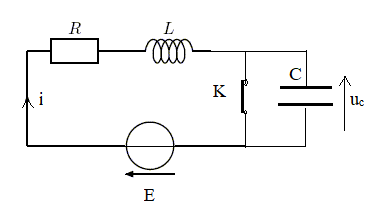
Le
condensateur d’un circuit 𝑅𝐿𝐶 s�rie, de capacit� 𝐶 = 20 μF, est mis
en court-circuit par un interrupteur 𝐾 depuis une
dur�e suffisamment longue pour que le r�gime soit �tabli (permanent).
Le circuit est aliment� par une source de tension
stationnaire id�ale de force �lectromotrice 𝐸. On ouvre 𝐾 � un
instant pris comme origine temporelle. La bobine du circuit
poss�de une inductance 𝐿 = 50 mH. On note 𝑅 la r�sistance du
r�sistor, 𝑖 l’intensit� du courant �lectrique qui traverse la
bobine, et 𝑢
c, la tension aux bornes du condensateur
Lorsque 𝐾 est ouvert, le facteur de qualit� du circuit vaut 𝑄 = 10. On note
w0
la pulsation propre du circuit.
13. Calculer num�riquement 𝑅.
A) 0,002 ohm ;
B) 0,2 ohm.
C) 5 ohms.
Vrai.
D) 500 ohms.
LC
w02 = 1 ;
w0 = 1 /(LC)
� =1 /(0,05 x20 10
-6)
� =10
3 rad /s.
Q = L
w0 / R ; R = L
w0 / Q =0,050 x 10
3 / 10 =5 ohms.
14.Que peut-on dire de la pseudo-pulsation
w ?
On ouvre K : E = Ldi/dt +Ri + u
c.
i = dq / dt = C du
c / dt ;
di/ dt =C d
2u
c / dt
2 ;
E =LC d
2u
c / dt
2 +RCdu
c / dt + u
c.
E /(LC) =d
2u
c / dt
2 +R / L du
c / dt + u
c / (LC).
w0 = 1/(LC)
�. Q = L
w0 / R =(L / C)
� / R.
E
w02 =d
2u
c / dt
2 +
w0 / Q du
c / dt +
w02 u
c.
Equation caract�ristique de l'�quation diff�rentielle sans second membre ::
r
2 +
w0 / Q r +
w02 =E
w02 .
Discriminant :
D =(
w0 / Q)
2-4
w02 = 4
w02 (1/(4Q
2)-1) < 0 car Q = 10.
Solutions de cette �quation caract�ristique :
-
w0 / (2Q) � j
w0 (1/(4Q
2)-1)
�.
Pseudo-pulsation:
w =(-
D)
� / 2 =
w0 (1-1/(4Q
2))
�.
Or 1/(4Q
2) <<1 donc (1-1/(4Q
2))
�~1-1/(8Q
2).
w ~
w0 |1-1/(8Q
2) ].
R�ponse A.
15. Que valent l’intensit� 𝑖(0
+) et la tension 𝑢
c
(0
+) � l’instant 𝑡 = 0
+ succ�dant imm�diatement � l’ouverture de 𝐾 ?
A) 𝑖(0
+)=0.
B) 𝑖(0
+)=E / R.
Vrai.
C) 𝑢
c
(0
+)=0
Vrai.
D) 𝑢
c
(0
+) = E.
A
t < 0 : le r�gime permanent est �tabli.
La tension aux bornes de la bobine est nulle et E = Ri.
Par suite l'intensit� i(t) �tant une fonction continue 𝑖(0
+)=E / R.
A
t < 0 : la tension aux bornes du condensateur est nulle.
Par suite la tension u
c(t) �tant une fonction continue u
c(0
+)=0.
16. La tension aux bornes du condensateur �volue selon 𝑢
c
(𝑡) = exp(-t / (2
t)) [𝐴 cos(
wt) + 𝐵 sin(
w𝑡)]+ E, 𝐴, 𝐵 et
t
�tant des
constantes temporelles. Exprimer 𝐴 :
A) A = E ;
B) A = -E
vrai ;
C) A=0 ; D) A = �E.
𝑢
c
(0) =0 =A+E.
17. Exprimer 𝐵 :
i(t) =C du
c / dt = exp(-t / (2
t)) [𝐴 cos(
wt) + 𝐵 sin(
w𝑡)] (-1/(2
t))+exp(-t / (2
t)) [-𝐴
w sin(
wt) + 𝐵
w cos(
w𝑡)].
i(t=0) = -A / (2
t)+ 𝐵
w = E / R.
B = E /(R
w) +A / (2
tw)=E /(R
w) -E / (2
tw).
18. On attend suffisamment longtemps que le r�gime s’�tablisse puis, � un instant pris comme nouvelle origine des
temporelle, on ferme 𝐾. On retiendra, par convention, comme dur�e du r�gime transitoire, la dur�e n�cessaire pour
que 𝑖 atteigne 95 % de sa valeur finale (on indique que ln 20 ≈ 3). D�terminer la dur�e
trt du r�gime transitoire
succ�dant � la fermeture de 𝐾.
A) ~3L / R
vrai.
B) ~3RC
C) ~30 ms
vrai.
D) ~300 ���s.
En r�gime �tabli : u
c= E et i = 0.
Fermeture de K
: le condensateur se d�charge tr�s rapidement dans les fils ( maille de
droite). La r�sistance de ces conducteurs �tant tr�s faible,
t = rC ~0.
Puis on a un circuit RL : i(t=0) = 0.
Le courant s'�tablit avec une constante de temps
t' = L / R = 0,050 / 5 = 0,01 s = 10 ms.
E = Ldi /dt + Ri.
E / L = di /dt +R / L i.
Solution de cette �quation i = A exp(-t /
t')+ E / R.
i(0) = 0 = A+E / R ; A = -E / R.
i(t) = E/R(1-exp(-t /
t').
L'intensit� atteint 95 % de sa valeur finale E / R � :
0,95 = 1-exp(-t /
t') ; exp(-t /
t') =0,05.
exp(-t / 0,01) = 0,05 ; t = -0,01 ln(0,05) = 0,01 ln20~0,01 x3 ~0,03 s ~30 ms soit 3 L / R).
