La
Terre, assimilée à un corpuscule 𝑇 de masse M
T, possède une
orbite elliptique dans le référentiel héliocentrique. Ce
dernier, supposé galiléen, est centré sur le Soleil de masse M
S
, placé en O. On note A
p et A
a les positions
orbitales extrêmes
de T : le périhélie 𝐴
p et l’aphélie A
a. On
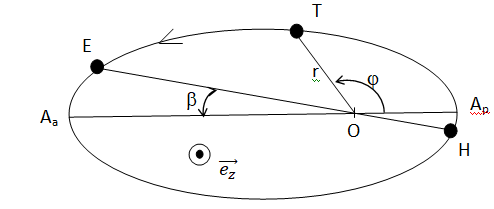
repère la position de T à l’aide du système de coordonnées polaires de
centre O : r=OT et
j.
Les angles sont orientés dans le sens de parcours de la trajectoire.
On pose r
p = OA
p et r
a = OA
a
et on note G la constante de Newton (dite de gravitation universelle).
On introduit v
p et v
a les
vitesses de T respectivement en A
p et A
a. Sur la
figure précédente, on a représenté la position H occupée par la Terre
au
début de l’hiver (solstice d’hiver), ainsi que la position E occupée
par la Terre au début de l’été (solstice d’été) à l’aide de
l’angle ß =12,2° .
L’origine (ou référence) de l’énergie potentielle gravitationnelle est
prise à l’infini et on note E
m l’énergie mécanique de T
dans le référentiel héliocentrique.
19. Que peut-on
affirmer ?.
A) r
pv
p
= r
av
a ;
vrai.
B) r
p2v
p
= r
a2v
a ;.
C) E
m(A
p)
diffère de E
m(A
a).
Vrai.
D) E
m(A
p) = E
m(A
a).
Vrai.
L'interaction de gravitation est une force centrale :
- l'énergie mécanique se conserve. E
m(A
p) = E
m(A
a).
- le moment cinétique se conserve.
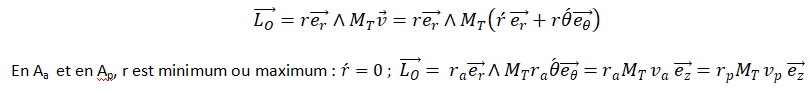 20.
20. Exprimer v
a.
Conservation de l'énergie mécanique :
½M
T v
a2 -GM
T M
S
/ r
a =½M
T v
p2 -GM
T
M
S / r
p .
½v
a2 -G M
S / r
a =½ v
p2
-G M
S / r
p .
Or v
p =r
a / r
p v
a.
½v
a2 -G M
S / r
a =½ (r
a
/ r
p v
a)
2 -G M
S
/ r
p .
½v
a2 [1-(r
a / r
p )
2
]=G M
S [ 1/ r
a-1/ r
p]= G M
S
[ (r
p - r
a) / (r
ar
p)].
v
a2 =2G M
S [ (r
p - r
a)
/ (r
ar
p)] / [1-(r
a / r
p )
2
].
v
a2 =2G M
S [ (r
p - r
a)
/ (r
ar
p)] / [ (r
p2-r
a2)
/ r
p 2 ].
v
a2 =2G M
S / r
a / [ (r
p
+ r
a) / r
p ].
v
a2 =2G M
S r
p / [r
a
(r
p + r
a) ].
v
a ={ 2G M
S r
p / [r
a
(r
p + r
a) ] }
½. Réponse
D.
21. Exprimer L
z.
L
z =M
T r
a v
a =M
T r
a { 2G M
S r
p / [r
a
(r
p + r
a) ] }
½= M
T { 2G M
S r
ar
p /
(r
p + r
a) }
½. Réponse
B.
22. L’équation polaire de la trajectoire de la Terre est la suivante : r = p /(1+e cos
j)
où e et p sont deux constantes temporelles
indépendantes de r et de
j. Sachant que e << 1, que peut-on affirmer ?
A) L
z / M
T ~p
2(1+ e cos
j)
j' ;
B) L
z / M
T ~p
2(1- e cos
j)
j' ;
C) L
z / M
T ~p
2(1+2 e cos
j)
j' ;
D) L
z / M
T ~p
2(1-2 e cos
j)
j' .
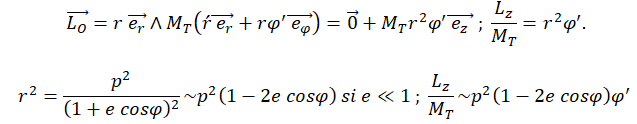
Réponse
D.
23. On rappelle l’égalité suivante, dans laquelle g'(
j) désigne la dérivée d’une fonction g(
j) par rapport à
j :
g'(
j)
j' =d g(
j) / dt.
En déduire la durée
t1
nécessaire pour que T passe de H à E, c’est-à-dire la durée qui s’écoule entre le solstice d’hiver et
le solstice d’été.
On pose g'(
j) =1-2e cos
j ; g(
j) =
j-2e sin
j + A avec A une constante.
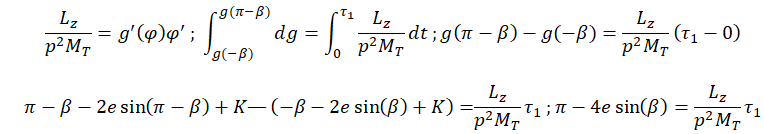
Réponse
D.
24. De même, exprimer la durée
t2
nécessaire pour que 𝑇 passe de E à H, c’est-à-dire la durée qui s’écoule entre le solstice
d’été et le solstice d’hiver.
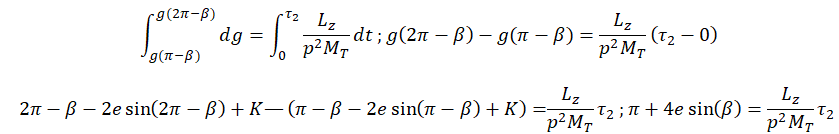
Réponse
C.