Masse accrochée entre deux ressorts,  concours ENAC pilote 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... On s’intéresse aux oscillations harmoniques d’un système simple constitué d’une masselotte, assimilée à un corpuscule 𝐴 (masse 𝑚), attachée à deux ressorts identiques (raideur 𝐾, longueur au repos L0 , masse négligeable) par une de leurs extrémités. L’autre extrémité de chaque ressort est fixée à un bâti. A l’équilibre, la longueur des ressorts est Le > L0. On cherche la pulsation propre des oscillations d’un tel système dans différentes configurations. Pour toutes les situations considérées dans cet exercice, on néglige les frottements. 1. Quelle est l’unité SI (système international des unités) et la dimension physique d’une pulsation propre ? A) s-1. B) rad s-1. Vrai. C) La dimension physique est celle de l’inverse d’une durée. Vrai. Un angle est le rapport de la longueur d'un arc de cercle au rayon du cercle. Un angle n'a donc pas de dimension physique. D) La dimension physique est celle d’un angle divisé par une durée. 2. Quelles sont les affirmations exactes ? A) Une pulsation au carré est homogène à une force par unité de masse.  B) Une pulsation au carré est homogène à une force par unité de longueur. C) Une pulsation au carré est homogène à une force par unité de masse et par unité de longueur. Vrai.  D) Une pulsation au carré est homogène au produit d’une masse et d’une force par unité de longueur. w2 = k / m.  k s'exprime en N  m-1. w2 s'exprime en N  m-1kg-1. 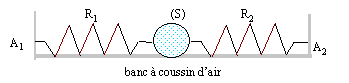On pose A1A2 = L. 3. On déplace 𝐴, par rapport à sa position d’équilibre 𝑂 (prise comme origine des coordonnées cartésiennes 𝑥 et 𝑦), d’une quantité initiale x0 << L0 selon la direction horizontale 𝑂𝑥  et on l’abandonne sans vitesse initiale. Le mouvement est astreint à demeurer horizontal. On observe alors un mouvement harmonique de pulsation w0,l . Quelles sont les expressions de w0,l et de la période T0 des oscillations correspondante ? A) w0,l = (2k / m)½. Vrai. B) w0,l = (2m / k)½. C) T0= (2k / m)½ / (2p). D) T0=2p (m / (2k))½ . Vrai. Les deux ressorts étant identiques : l1=l2. 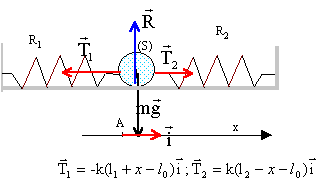longueur de R1 : l1+x = ½L-R+x longueur de R2 : l2-x = ½L-R-x La seconde loi de Newton s'écrit en projection sur l'axe Ax : -T1 + T2 = mx". -k(½L-R+x-l0) + k(½L-R-x-l0)=mx". 2kx=mx" soit x" + 2k/m x=0. On pose w0,l²= 2k/m ; w0,l = 2pf soit f = 1/(2p)[2k/m]½ ; T0= 1/f = 2p[2k/m]-½.   4. On écarte maintenant la masselotte, par rapport à sa position d’équilibre initiale, d’une quantité initiale 𝑦(0) << L0 , dans la direction transversale 𝑂𝑦 , laquelle est, comme la direction 𝑂𝑥, contenue dans le plan horizontal, et on l’abandonne sans vitesse initiale. Le mouvement est astreint à s’effectuer seulement selon cette direction transversale (𝑂𝑦). On observe alors, dans la direction 𝑂𝑦 seulement, un mouvement harmonique de pulsation propre w0,t . Quel est le rapport w0,t / w0,l  ?  A)  1. B) (1 − L0/Le)½. Vrai. C) (1 − Le/L0)½. D) (1 + Le/L0)½. 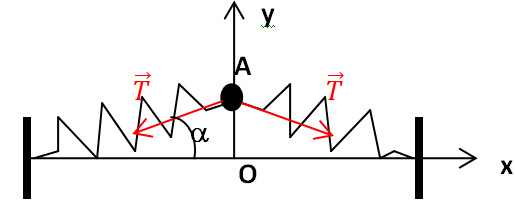Norme des forces execées par les ressorts : T =k [(Le2+y2)½-L0] = k [Le(1+(y / Le)2)½-L0]. Or y << Le, donc un développement limité à l'ordre 1 conduit à : (1+ (y / Le)2)½~ 1+½ y2 / Le2~ 1. T ~ k(Le-L0). Ecrire la seconde loi de Newton suivant l'axe Oy : m y" =-2T sin a.  a étant petit, sin a ~ tan a ~ y / Le. m y" +2 k(Le-L0)  / Le y = 0. my" +2 k(1-L0 / Le) y = 0. y" +2 k(1-L0 / Le)  / m y = 0. On identifie w0,t  =[2 k(1-L0 / Le)  / m]½. w0,t / w0,l  =(1-L0 / Le) ½. ... .... 5. La masselotte précédente et ses deux ressorts sont maintenant disposés verticalement, c’est-àdire dans la direction du vecteur champ de pesanteur. Quelle est la nouvelle pulsation propre w'0,t des oscillations si, comme précédemment, on écarte 𝐴, dans la direction 𝑂𝑧, d’une très petite quantité par rapport à la position d’équilibre (le mouvement est contraint à s’effectuer selon la direction verticale) ? A) w'0,t = w0,t Vrai. B) w'0,t =2 w0,t . C) w'0,t = w0,t / 2.  D) On ne peut rien dire a priori. La seconde loi de Newton s'écrit suivant l'axe (O, z) : k(L1-L0) - k(L2-L0) - mg = mz". k( L1 éq-z -L0) - k(L2 éq- L2 +z) - mg = mz". k(L1 éq-L0) -kz - k(L2 éq-L2)- k z -mg = mz". La masse étant au repos : T1 = k(L1 éq-L0) ; T2 = k(L2 éq-L0). -2kz  -mg= mz". z"+2k /m z =-g. La pulsation est inchangée.  6. Calculer la longueur des ressorts à l’équilibre si L0 = 10 cm, 𝑚 = 10 g et k = 10 N. m-1. La longueur totale entre les deux bâtis est 2L0 (on néglige la dimension de la masselotte). On prendra pour l’intensité du champ de pesanteur la valeur g ≈ 10 m. s-2. Le point 𝑂 est pris comme origine de l’axe vertical ascendant 𝑂𝑧. Parmi les réponses proposées, Le,h et Le,b désignent, respectivement, les longueurs à l’équilibre du ressort du haut et du ressort du bas.  A) Le,h =11 cm et Le,b =9 cm. B) Le,h =10 cm et Le,b =10 cm. C) Le,h =9 cm et Le,b =11 cm. D) Le,h =10,5 cm et Le,b =9,5 cm. Vrai. A l'équilibre z" =0 ;  k(Le,h-L0) - k(Le,b-L0) - mg =0. 10(Le,h-0,1) - 10(Le,b-0,1) = 0,1. Le,h-0,1 - Le,b+0,1 = 0,01. Le,h - Le,b = 0,01. De plus Le,h + Le,b = 0,2. 2Le,h =0,21 ; Le,h =0,105 m.

menu