Freinage par induction,  concours ENAC pilote 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Un cadre métallique filiforme 𝐴𝐵𝐶𝐷, de forme carrée (côté 𝑎), est abandonné sans vitesse initiale, par rapport au référentiel ℛ du laboratoire supposé galiléen, dans le champ de pesanteur terrestre supposé uniforme.  Au cours de sa chute, ce cadre pénètre soudainement, à un instant pris comme origine du temps, dans une région, supposée illimitée, de l’espace (𝑧 > 0) où règne un champ magnétique 𝐵 uniforme et stationnaire.  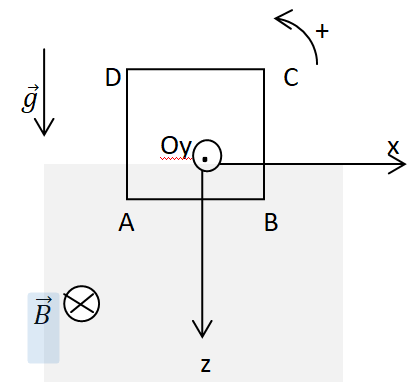Dans cet exercice, on désignera par zA la cote du point A. On considère en outre que l’inductance propre du cadre est négligeable. 13. On oriente le cadre dans le sens trigonométrique. On note t1 l’instant à partir duquel le cadre se trouve entièrement immergé dans la région 𝑧 > 0. Quelle est l’expression de la tension électromotrice (ou force électromotrice) e(t) induite au cours de la chute du cadre ? Si t < 0 et si t > t1, le flux du champ magnétique B ne varie pas ; donc e(t) = 0. Entre les dates t=0 et t =t1, la surface (S = a zA) du cadre plongé dans le champ magnétique varie. 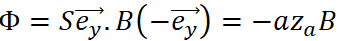Il en sera de même du flux magnétique F : D'où l'apparition d'une fem e(t) = -dF/dt = B a dzA /dt = B a zA z'A. Réponse B.   14. Le cadre métallique présente une résistance R. Déterminer l’expression de la force de Laplace F à laquelle est soumis le cadre. Aucun courant induit ne circule dans le cadre si t <0 et si t > t1. La force de Laplace est donc nulle. Sinon un courant d'intensité i = e(t/ / R circule dans le cadre dans le sens positif choisi. Dans DA, le courant descend et dans BC le courant monte : les forces de Laplace correspondantes se compensent. 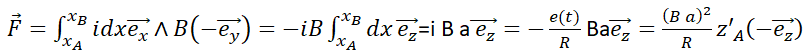Force de Laplace sur le côté AB :   Réponse C.   15. Établir, par rapport à R, l’équation différentielle du mouvement de A, le cadre étant supposé être en translation rectiligne, au cours de sa chute pour les instants compris entre l’instant initial et t1 . Le principe fondamental de la dynamique en projection sur l'axe Oz donne : mg-(Ba)2 / R z'A = m z"A. z"A+(Ba)2 / (mR) z'A =g. On pose t = mR/ (Ba)2, constante de temps. Réponse B. 16. Calculer t si B = 1 T, a = 5 cm, m=0,1 kg et R = 10 ohms. t =0,1 x10 / (0,05)2 =400 s. Réponse B. ... .... 17. Déduire de la question précédente la loi d’évolution de la vitesse z'A (t) sachant que la vitesse initiale est  v0. z"A+1 / t  z'A =g. Solution particulière z'A =g t. Solution générale de l'équation sans second membre : z'A= A exp(-t / t) avec A une constante. Solution générale : z'A= A exp(-t / t) +g t. A t=0 : v0 = A+g t. z'A=( v0-g t )exp(-t / t) +g t. Réponse A. 18.  Le cadre ABCD présente un interrupteur K qui permet de modifier le circuit fermé dans lequel pourrait circuler un éventuel courant induit :  si K est en position 1 (point K1 ), le circuit fermé est la spire rectangulaire AMK1D ; si K est en position 2 (point K2), le circuit fermé est la spire rectangulaire 𝐴𝐵𝐶𝐷. Que peuton dire sur e(t) si on maintient le cadre immobile et on commute soudainement K de la position 1 à la position 2 ? Ici encore, le cadre est orienté dans le sens trigonométrique. Si l'interrupteur bascule de K1 à K2, la surfce immergée S du circuit augmente. Le vecteur surface et le champ magnétique étant colinéaires et de sens contraire, le flux diminue. dF / dt < 0 et donc e(t) >0. .

menu