Mathématiques, concours Geipi Polytech 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. 29 points Première partie – Fonctions Dans cette partie, a et b sont des nombres réels. Le plan est muni d’un repère orthonormé. 1.1 Les réels a et b sont strictement positifs.ln(a+b) =  A) ln(a) × ln(b) . B) ln(a) + ln(𝑏) . C) ln(a) + ln(1+(1 + b / a ) vrai. ln[1+(1 + b / a ]=ln[(a+b) / a] = ln(a+b) -ln(a). ln(a) + ln(1+(1 + b / a )  = ln(a+b).  1.2- On peut calculer ln(𝑥2 − 1) sur :  A) ]0 ; +∞[ . B) ]−1 ; 1[ . C) ]−∞ ; −1[ ∪ ]1 ; +∞[  vrai. D) ]e−1 ; +∞[ . x2-1 doit être strictement positif soit x appartenant à : ]−∞ ; −1[ ∪ ]1 ; +∞[  1.3- Si f et g sont deux fonctions définies sur ]-∞ ; a[ ∪ ]a ; +∞[ et telles que : quand x tend vers a, f(x) tend vers +oo et g(x) tend vers 0+, alors quand x tend vers a : A) f(x) / g(x) tend vers 0+ . B)  f(x) / g(x) tend vers +∞ vrai . C) f(x) x g(x) tend vers 0+ . D) f(x) x g(x) tend vers +∞. 1.4- Si f est une fonction définie sur l’intervalle ]a ; +∞[ et telle que quand x tend vers a, f(x) tend vers +∞, alors :  A) La courbe représentative de f dans le repère R admet une asymptote horizontale. B) La courbe représentative de f dans le repère R admet une asymptote verticale.  vrai. C) La fonction f est décroissante sur ]a ; +∞[. 1-5- f est une fonction définie et dérivable sur ℝ telle que f(1) = 3 qui vérifie, pour tout nombre réel x, f '(x) + 2 f (𝑥) = 4. * On peut en déduire que : A) f ′ (1) = −2 vrai. B) f ′ (1) = 10 . C) f ′ (1) = 1 . f '(1) + 2 f (1) = 4. f '(1) +6=4 ; f '(1) = -2 * Une équation de la tangente à la courbe représentative de f dans le repère R au poinnt d’abscisse 1 est : D) 𝑦 = −2𝑥 + 3 . E) 𝑦 = 10𝑥 + 3 . F) 𝑦 = 𝑥 + 2 . G) 𝑦 = −2x + 5 vrai. f '(1) = -2  coefficient directeur de la tangnente au point d'abscisse 1. y = -2x+b. Le point de coordonnées (1 ; f(1) =3 ) appartient à la tangente. 3=-2+b ; b = 5. 1-6- f est une fonction dérivable sur l’intervalle ]a ; b[ contenant c. La courbe représentative de f dans le repère R admet au point d’abscisse c une tangente horizontale. On peut en déduire que : A) f(𝑐) = 0. B) f admet en c un maximum ou un minimum local qui vaut f(𝑐).  C) L’équation f(𝑥) = c admet une unique solution sur l’intervalle ]a ; b[.  D) f '(c) = 0. Vrai. 1.7- f est une fonction continue sur l’intervalle [a ; b]. Quelles sont les propositions vraies ? A) Si f(𝑎) × f(𝑏) > 0, alors f s’annule sur l’intervalle [a ; b].  B) Si c ∈ ]a ; b[, alors f(c) est compris entre f(a) et f(b).  C) Si k est un nombre réel compris entre f(a) et f(b), alors l’équation f(x) = k admet au moins une solution sur l’intervalle [a ; b]. Vrai.  1.8- f est une fonction deux fois dérivable sur l’intervalle [a ; b]. On note C la courbe représentative de f dans le repère R, A le point de C d’abscisse a et B le point de C d’abscisse b. On suppose que f  ''(x) > 0 sur l’intervalle [a ; b]. On peut en déduire que : A) f est croissante sur [a ; b].  B) f ' est croissante sur [a ; b] vrai. . C) f est convexe sur [a ; b]. vrai.  D) C est en-dessous du segment [AB]. vrai. Deuxième partie : suites numériques. 1-9- On considère une suite arithmétique (un) telle que u1 = 0 et u10 = 10. On peut en déduire que :  A) La raison de cette suite est égale à 1.  B) u19 = 20. vrai. C) Cette suite est convergente.  D)u1 + u2 + ⋯ + u10 = 50. Vrai. u1 = 0 ; u2 = r ; u3 =2 r ; u4 = 3r  ...u10 =9 r. u10-u1=10 = 9 r. La raison est égale à r = 10 /9. u19 = u1 + 18r = 0 +18 x 10 /9=20. (u1+u10)x n) / 2=(0+10) x10 /2 = 50.  1-10- On considère la suite (u𝑛) définie pour tout entier naturel n, par : u𝑛 = 5 − (5 /4)𝑛 . On a :  A) La suite (un) est géométrique de raison 5/ 4 .  B) La suite (un) est arithmétique de raison 5/ 4 . C) La suite (un) est décroissante. Vrai.  D) en plus l'infini, la limite de (un) est égale à 5 . un+1-un = -(5 /4)n+1+(5/4)n =(5 /4)n(1-5/4) < 0. La suite est décroissante. En plus l'infini (5/4)n tend vers plus l'infini et un tend vers moins l'infini. Troisième partie – Probabilités Dans cette partie, W désigne l’univers d’une expérience aléatoire E et P désigne une probabilité sur W. 1-11- On considère deux événements quelconques A et B. La probabilité P(A ∩ B) est égale à :  A) P(A) × P(B). B) P(A) + P(B). C) P(A ∪ B) − P(A ∩ nonB) − P(nonA∩ B ). Vrai  D) P(A) + P(B) − P(A ∪ B) vrai .1-12- On considère une variable aléatoire X qui prend ses valeurs dans l’ensemble {0, 1, 10}.  On donne les probabilités : P(𝑋 = 0) = 1/ 2 et P(X = 10) = 1/ 6 . On peut en déduire que :  A) P(X = 1) = 2/ 3 . B) P(X = 1) = 1 /3 vrai. C) E(X) = 2 vrai . D) E(𝑋) = 11 / 3 . P(X=1) = 1-P(X=0)-P(X=10)=1-1/2 -1 /6 =2/6=1/3. E(X) = 0 x1/2 + 1 x1 /3 +10 x1 /6 = 12 /6 =2. Quatrième partie – Géométrie dans le plan. 1-13- a et b sont des réels non nuls. On considère les points A, B, C et D de coordonnées respectives dans un repère orthonormé R : A(a ; a), B(a ; -a), C(−a ; b) et D(−a ; 0). Quelles sont les propositions vraies ?  A) Les droites (AB) et (DC) sont sécantes. B) Les droites (AB) et (DC) sont parallèles. Vrai.  C) Le quadrilatère ABCD est un parallélogramme si et seulement si b = 2a. D) Le quadrilatère ABCD est un parallélogramme si et seulement si b = −2a. Vrai. Exercice II (26 points). On pourra admettre les résultats de la première partie pour traiter la deuxième. 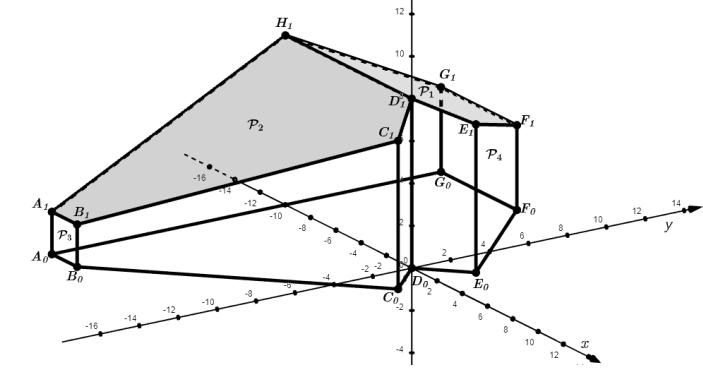La figure  représente un bâtiment.  La toiture est constituée de deux pans plans : P1 le plan (H1D1E1) et P2 le plan (C1D1H1). Les plans P3 et P4  sont parallèles. Les plans contenant les sept façades sont orthogonaux au plan de la dalle.  Première partie 1- Justifier que les droites (A0B0) et (F0G0) sont parallèles. P3 et P4 son parallèles et orthogonaux au plan de la dalle, noté P0. A0B0 : intersection de P3 et P0. F0G0 : intersection de P4 et P0. Par suite les droites (A0B0) et (F0G0) sont parallèles.  2- Justifier que la droite (D1H1) est parallèle aux droites (A1B1) et (F1G1). A0B0B1A1 est un rectangle : donc(A0B0) est parallèle à (A1B1). G0F0G1F1 est un rectangle : donc(G0F0) est parallèle à (F1G1). De plus (A0B0) et (F0G0) sont parallèles. Donc les droites (A1B1) et (F1G1) sont parallèles. Les plans P1 et P2 se coupent selon la droite (D1H1). (A1B1) appartient au plan P2 ; (F1G1) appartient au plan P1. (A1B1) et (F1G1) sont parallèles. Les plan P1 et P2 sont sécants selon D1H1. Théorème du toit : si une droite (A1B1) de P2 est parallèle à une droite (F1G1) de P4, alors la droite intersection des deux plans est parallèles à (A1B1) et (F1G1). Seconde partie. L’espace est rapporté à un repère orthonormé. On donne les coordonnées suivantes : A0(−10 ; −12 ; 0), B0(−8 ; −12 ; 0), C0(2 ;−2 ; 0), D0(0 ; 0 ; 0), E0(2 ; 2 ; 0), F0(−4 ; 8 ; 0), G0(−10 ; 8 ; 0), C1(2 ;−2 ; 7), D1(0 ; 0 ; 8), E1(2 ; 2 ; 7), H1(−10 ; 0 ; 8). 3- Donner les coordonnées des vecteurs suivants. 4- Montrer que le vecteur n de coordonnées(0 ; 1 ; 2) est un vecteur normal au plan P1. 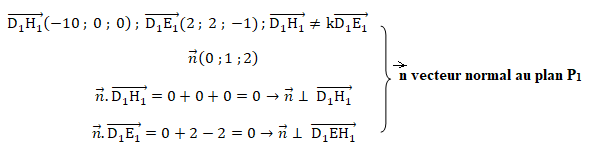5- En déduire une équation cartésienne du plan P1. Justifier la réponse. 0x +1y +2z +d = 0 soit y+2z+d=0. D1 appartient  à ce plan : 2 *8+d=0 ; d = -16. y+2z-16=0.  6- Le point F1 a pour coordonnées (−4 ; 8 ; z1). Déterminer la valeur de z1. Justifier la réponse. F1 appartient au plan P1. 8+2z1-16 = 0 ; z1 =4.  7- En déduire la longueur F0F1. Aucune justification n’est demandée. F0F1 = [(-4+4)2+(8-8)2+42 ] ½ =4.  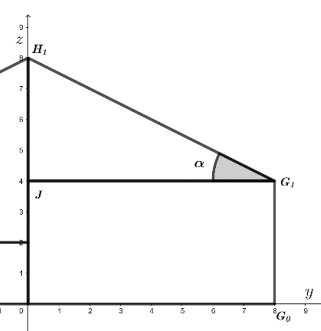La façade arrière du bâtiment est schématisée ci-dessous. La droite verticale issue de H1et la droite horizontale issue de G1se coupent en un point J. La pente du toit est la mesure a, exprimée en degrés, de l’angle JG1H1. 8- Déterminer la valeur de tan a. Aucune justification n’est demandée. tan a =H1J / JG1 = 4 / 8 = 0,5. 9- Dans cette région, la pente d’un toit doit être comprise entre 33° et 45°. La toiture du bâtiment respecte-t-elle les normes de la région ? Justifier la réponse. a ~ 27 °. La pente du toit ne respecte pas les normes. 10- On admet qu’une équation cartésienne du plan P2 est donnée par y − 2z + 16 = 0. Vérifier qu’une équation cartésienne du plan (B0C0C1) est donnée par x − y − 4 = 0. xB0-yB0-4 = -8+12-4=0 est vérifiée. xC0-yC0-4 = 2+2-4=0 est vérifiée. xC1-yC1-4 = 2+2-4=0 est vérifiée. Les coordonnées de ces trois points non alignés vérifient l'équation x-y-4=0. L'équation cartésienne du plan P2 est donnée par y − 2z + 16 = 0. 11- En déduire une représentation paramétrique de la droite (B1C1). Aucune justification n’est demandé. B0(−8 ; −12 ; 0) ; B1(−8 ; −12 ; z) ; C1(2 ;−2 ; 7). Coordonnées d'un vecteur directeur de (B1C1) : (10 ; 10 ; 7-z). B1 appartient au plan P2 : z = ½y +8= -6+8=2. Coordonnées d'un vecteur directeur de (B1C1) :(10 ; 10 ; 5). ou (2 ; 2 ; 1) Représentation paramétrique de cette droite: x= 2 t +xC1 =2t+2. y = 2t +yC1 =2t-2.  z =t+zC1 =t+7. Une représentation paramétrique de la droite (A1H1) est donnée par : x = −10 ; y = 2k ;  z = 8 +k ,avec k réel. On admet de plus que les droites (A1H1) et (B1C1) sont sécantes. 12- On souhaite prolonger le pan de toit (A1B1C1D1H1) jusqu’au sol. Cela est-il possible ? Justifier la réponse. Intersection des droites (A1H1) et (B1C1) : -10 = 2t+2 ; t = -6. Par suite z = 1 m. Ces droites se coupent à une altitude de 1 m. Ce pan de toit ne pourra pas être prolongé jusqu'au sol. ... .... Exercice 3. 25 points On considère la fonction f définie pour tout réel x , par : f(x) = −(1 + x2)e-𝑥 . Dans le plan muni d’un repère orthonormé, on note Cf la courbe représentative de f. 1- Donner la limite de f(x) en moins l'infini. Aucune justification n’est attendue. e-𝑥  tend vers plus l'infini et 1+x2 tend vers plus l'infini. Par produit des limites, f(x) tend vers plus l'infini si x tend vers moins l'infini. 2- Donner la limite de f(x) en plus l'infini. Justifier. e-𝑥  tend vers zéro et 1+x2 tend vers plus l'infini. Par produit des limites, f(x) tend vers zéro si x tend vers plus l'infini. 3- On en déduit que Cf admet une asymptote D au voisinage de +∞. Donner une équation de D. Préciser la position de Cf par rapport à D. Aucune justification n’est demandée. L'axe des abscisses est asymptote à Cf. y = 0. e-𝑥 >0 ; −(1 + x2) <0 ; la courbe est en dessous de l'asymptote. 4-  f ' désigne la dérivée de f. Déterminer les réels a et b tels que, pour tout réel x, f '(x) = (ax+b)2e-𝑥. Détailler le calcul. On dérive f(x) en posant u = -(1+x2) et v = e-x. u' = -2x ; v' = -e-x. u'v+v'u = e-x(-2x+1+x2) =(x-1)2 e-x. a = 1 ; b = -1. 5- Donner l’ensemble  des solutions de l’équation f '(x) = 0. Aucune justification n’est demandée. Une solution unique x = 1. 6- Compléter le tableau des variations de la fonction f sur ℝ. 7- Soient A et B les points de Cf d’abscisses respectives xA = 1 et xB = 0. TA et TB désignent les tangentes à Cf aux points A et B. Donner, sans justification, des équations de TA et de TB. TA : coefficient directeur f '(1) =0 ; Le point A de coordonnées (1 ; f(1) =-2e-1) appartient à la tangente. Equation de TA : y = b = -2e-1. TB : coefficient directeur f '(0) =1 ; Le point B de coordonnées (0 ; f(1) =-1) appartient à la tangente. Equation de TB : y =x+ b  ; -1 = 0+b ; b = -1. y = x-1. 8- QCM Sur une figure, on place les points A et B, on trace la droite D, les tangentes TA et TB puis la courbe Cf. Parmi celles proposées ci-dessous, laquelle représente la figure obtenue ? 9 - Justifier que l’équation f(x) = −3 admet une unique solution dans l’intervalle [−1 ; 0].  f(-1) =-2e à f(0) = -1. Sur l'intervalle [-1 ; 0] la fonction est continue et strictement croissante à valeurs dans [-2e ; -1]. -3 appartient à cet intervalle. D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(x) = -3 admet une solution unique.  10 - QCM On considère l’algorithme ci-dessous dans lequel :a et b sont deux réels tels que a < b. a= −1  b= 0 Tant que |b − a| > 0,3 x= (a+b)/ 2 Si g(a)g(x) > 0  alors a=x  sinon b =x  Fin si Fin tant que x =(a+b) /2 Afficher x  x est un nombre réel. g est la fonction définie sur [−1 ; 0] par g(x) = f(x) + 3 . On applique cet algorithme à la fonction g. Quelle valeur contient la variable x après l’exécution de l’algorithme ? A) −0,75 ; B) −0,5 ; C) −0,625 vrai ; D) −1. a -1 -1 -0.75 b 0 -0,5 -0,5  |b − a| > 0,3 vrai vrai faux x -0,5 -0,75 0,625 g(a) négatif négatif g(x) positif négatif g(a) g(b) >0 faux vrai ..

menu