Physique, Concours interne  ing�nieurs de l'industrie et des mines 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

.
. . .

.
.
.. ..
......


...
Exercice 1.
On consid�re une onde lumineuse, dans l'air, r�fl�chie sur une couche mince d'�paisseur (t), d'indice n1, d�pos�e sur un mat�rieau d'indice n2. F1 est l'onde r�fl�chie sur la couche mince, F2 l'onde r�fl�chie � l'interface mat�riau / couche mince apr�s travers�e de celle-ci. On consid�re que l'angle d'incidence de l'onde lumineuse est quasi normal.

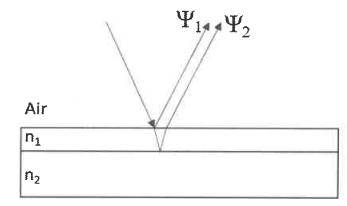
On note :
F1=E1 sin (a1-wt) avec a1 = kx+e1.
F2=E2 sin (a2-wt) avec a2 = kx+e2.
E1/E2 est respectivement l'ampliitude de l'onde F1/F2 : k est le nombre d'onde ; w la pulsation ; e la phase � l'origine ; x la distance depuis la source.
Coefficient de r�flexion � l'interfce de  2 milieux d'indice n et n' : R = (n'-n) / (n'+n).
1. En utilisant l'identit� sin( A-B) = sin A cos B - cos A sin B, montrer que l'on peut �criire F' = F1+F2 = E sin( a-wt). Commenter ce  r�sultat.
sin (a1-wt) = sin a1 cos (-wt)- cos a1 sin(-wt)= sin a1 cos (wt) + cos a1 sin(wt).
 sin (a2-wt) = sin a2 cos (-wt)- cos a2 sin(-wt)= sin a2 cos (wt) + cos a2 sin(wt).
F1+F2 =E1 sin (a1-wt) +E2 sin (a2-wt).
F1+F2 =E1 [sin a1 cos (wt) + cos a1 sin(wt) ] +E2 [sin a2 cos (wt) + cos a2 sin(wt) ] .
F1+F2 =cos (wt) [E1 sin a1 +E2 sin a2 ] + sin(wt)[E1 cos a1 +E2 cos a2 ].

E sin( a-wt) = E [ sin a cos (wt)-cos a sin (wt)].
On identifie : E sin a =E1 sin a1 +E2 sin a2 .
 E cos a = -[E1 cos a1 +E2 cos a2 ].
L'onde r�fl�chie a m�me fr�quence que l'onde incidente. Par contre son  amplitude n'est pas constante.

2. Exprimer a en fonction de E1, E2, a1 et a2.
 tan a = - [E1 sin a1 +E2 sin a2] / [E1 cos a1 +E2 cos a2 ].

3. Montrer que E2 = E12+E22+2E1E2 cos(a2-a1).
 E2 sin2 a =E21 sin2 a1 +E22 sin2 a2 +2E1E2sin a1 sin a2 .
E2 cos2 a =E21 cos2 a1 +E22 cos2 a2 +2E1E2cos a1 cos a2 .
On ajoute : E2 = E12+E22+2E1E2 ( sin a1 sin a2 +cos a1 cos a2).
 sin a1 sin a2 +cos a1 cos a2)= cos(a2-a1).

4. Expliciter la diff�rence de chemin optique d entre les ondes F1 et F2.
L'angle d'incidence de l'onde lumineuse est quasi normal, la diff�rence de chemin optique est �gale � 2 �paisseur de la couche mince.
d = 2 t.
 5. On souhaite r�aliser un filtre anti-reflet pour des lunettes de vue. Quelle est l'�paisseur minimum de la couche mince � d�pooser sur les verre permettant de minimiser les r�flexion pour une onde lumineuse de longueur d'onde  l ? Donner un ordre de grandeur approximatif.
Les interf�rences doivent �tre destructrices.
d = 2 t =(2k+1) l /2.
tmini = l / 4 soit 500 / 4 = 125 nm pour une onde de longueur d'onde 500 nm, la plus sensible pour l'oeil humain.
6. M�me avec une �paisseur id�ale, un anti-reflet de fluorure de magn�sium  ( n=1,38) ne pourra pas minimiser enti�rement les r�flexions sur un verre d'indice n = 1,53. Pourquoi ? Que est la fraction de lumi�re r�fl�chie ?
Seule la r�flexion est entierement supprim�e en incidence normale pour des longueurs d'onde proches de 500 nm.
 Coefficient de r�flexion � l'interfce de  2 milieux d'indice n et n' : R = (n'-n) / (n'+n).
R = (1,53-1,38) / ((1,53 +1,38) =0,15 / 2,91 ~0,05.
7. Comment choisir l'indice de la couche mince pour que toute la lumi�re soit transmise ? Quelle valeur de n1 faudrait-il choisir si n2 = 1,5 ?
Les ondes r�fl�chies qui interf�rent de mani�re destructive ( d�phasage p ) doivent avoir la m�me amplitude E1=E2.
E2 = E12+E22+2E1E2 cos(p) = 0.
Coefficient de r�flexion air - couche anti-reflet d'indice n1 : R1 = (n1-1) /  (n1+1).
Coefficient de r�flexion couche antireflet d'indice n1  verre d'indice n2 : R2 = (n2-n1)/ (n2+n1).
La r�flexion est annul�e ( toute la lumi�re est transmise) si : R1 = R2 .
(n1-1) /  (n1+1) = (n2-n1)/ (n2+n1).
n1 n2-n1 +n2-n12= n1n2 +n12-n2-n1.
 2n12=2n2.
n1 = n2� =1,5�~1,22.
8. Le filtres anti-reflet peuvent �tre constitu�s de plusieurs couches. Quel est l'int�r�t et l'inconv�nient principal d'augmenter le nombre de couches ?
Int�r�t : les propri�t�s anti-reflet sont conserv�es au voisinage des longueurs d'onde proches des UV et des IR, c'est � dire sur toute la gamme du visible.

...
....

 Exercice 2.
  On consid�re une �toile assimil�e � une sph�re de gaz en �quilibre hydrostatique. La densit� de l'�toile varie en fonction de la distance r, et la masse d'une couche d'�paisseur de est dMr = 4 p r2 r(r) o� r(r) est la masse volumique � la distance r.
La pression au sein de l'�toile est due � la pression des particules ( pression gazeuse) et celle des photons ( pression de rayonnement ). si l'on note P(r) la pression s'appliquant en r sur l'�l�ment de volume consid�r� et P +dP la pression en r+dr, on peut montrer que la force due � la pression(P) s'appliquant sur cet �l�ment est -dPdA.

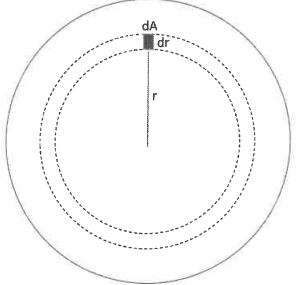
1 Consid�rant que la force gravitationnelle et la pression s'�quilibre, exprimer dP en fonction de G, Mr, r, r et dr.
dP / dr = -GMrr / r2.
GMr / r2 : intensit� du champ gravitationnel au rayon r.
2. En d�duire l'ordre de grandeur de la pression au centre du soleil en pascals et en atmosph�res. On consid�rera dans la suite de l'exercice r constant �gal � la masse volumique moyenne. Pour le soleil :
R = 6,96 108 m ; M =1,99 1030 kg ; G = 6,674 10-11 m3 kg-1 s-2.
r = M / (4 /3pR3)
Int�grer la pression du centre Pc= P(0) vers la surface PR ~ 0.

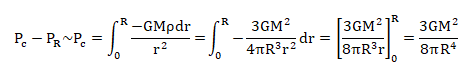
Pc = 3GM2 / (8pR4 )=3 x6,674 10-11 x(1,99 1030)2 / [8 x3,14(6,96 108)4 ]=1,3 1014 Pa ou 1,3 109 atmosph�res.


3. On suppose que le gaz est constitu� d'hydrog�ne. En partant de la loi des gaz parfaits, donner l'expression de la pression gazeuse Pg en fonction de la constante des gaz parfaits, du nombre d'Avogadro, de la masse volumique, de la temp�rature et de la masse d'un atome d'hydrog�ne �H= 1,67 10-27 kg. En d�duire l'ordre de grandeur de la temp�rature au centre du soleil. Commenter cette approximation.
PgV = nRT.
Pg = nRT / V.
n = masse d'hydrog�ne / masse molaire H2.
masse d'hydrog�ne = volume fois masse volumique.
n / V = masse volumique / masse molaire H2.
n / V =masse volumique / (Na �H) =  r / (Na �H).
Pg = r / (Na �H) RT.
T = Pg Na �H / (r R).
r = M / (4 /3pR3) =3 x1,99 1030 / (4 x3,14x(6,96 108)3) =1,4 103 kg m-3.
T = 1,3 1014 x6,023 1023 x 1,67 10-27 / (1,4 103 x8,314) =
T = 1,1 107 K.
Valeur r�elle : 1,5 107 K.
Cette approximation donne l'ordre de grandeur de la temp�rature au centre du soleil.

4. Quelle est l'�nergie potentielle d'une couche situ�e � la distance r du centre de l'�toile en fonction de G, r et � ?
Surface de la couche  : 4 p r2 ; �paisseur : dr.
Volume de la couche dt = 4 p r2 dr.
Masse de la couche de masse volumique � : dm = �dt.
Masse de l'astre : m(r) = � 4 / 3 pr3.
Pour une couche situ�e � l'infini, son �nergie potentielle gravitationnelle est nulle.
Pour une couche d�pos�e � la surface de l'astre, � la distance r du centre :
dEp = -Gm(r) dm / r = -G�2 16 / 3 p2  r4 dr.
Int�grer entre 0 et R : Ep = -G�2 16 / 15 p2  R5.
De plus � =M / (4 /3 pR3).
Ep = -3GM2 / (5R).

5. Quelle serait l'�nergie lib�r�e si l'�toile pouvait se contracter jusqu'� dispara�tre compl�tement ? Donner le r�sultat en fonction de G, M et R ( le rayon de l'�toile) avant de le calculer.
Si la sph�re se contracte ( R diminue) et l'�nergie gravitationnelle diminue ( donc de l'�nergie est lib�r�e ).
Quand un gaz est en �quilibre gravitationnel, l'�nergie interne du gaz ( �nergie cin�tique des particules ) est �gal � -�Ep .
La moiti� de l'�nergie gravitationnelle lib�r�e par la contraction reste dans l'�toile pour chauffer le gaz et maintenir l'�quilibre. L'autre moiti� est lib�r�e par rayonnement.
E = 3GM2 / (10R).
Dans le cas du soleil : E =3 x 6,674 10-11 x(1,99 1030)2 /(10 x6,96 108) =1,1 1041 J.

6. La luminosit� du soleil (L) �tant d'environ 3,86 1026 W, comparer le r�sultat pr�c�dent � l'�ge de la terre.
Si la lumisosit� est constante au cours du temps : 1,1 1041 / (3,86 1026) ~2,8 1014 s ou 9 106 ans.
�ge de la terre : 4,5 109 ans.
Ces r�sultats �tant tr�s diff�rent, la luminosit� n'est pas constante.

7. On onsid�re que le soleil se comporte comme un corps noir. Pour un tel corps, la loi suivante relie le rayonnement thermique � la temp�rature T.
E = s T4 avec s = 5,67 10-8 W m2 K-4.
E repr�sente l'�mittance. Quelle est la dimension de E ? En d�duire la temp�rature de surface du soleil.
E s'exprime en W m2 K-4 K4 = W m2.
Surface du soleil : 4 p R2 =4 x3,14 x(6,96 108)2 = 6,1 1018 m2.
E =   3,86 1026 / (6,1 1018)=6,3 107 W m-2.
T4 = 6,3 107 /( 5,67 10-8 ) =1,1 1015 .
T =5,8 103 K.

  
menu