Un saut parfait, bac général Asie  2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Le saut au ski Freestyle est une discipline olympique qui est l'équivalent sur neige du trampoline ou de la gymnastique. Les skieurs s'élancent à plus de 60 km.h-1 sur une rampe et montent d une hauteur suffisante pour réaliser des figures. La performance est jugée par rapport à la qualité d'exécution et de réception ainsi que par rapport à la hauteur et à la portée du saut.  Pour une m6me valeur de la vitesse initiale, les caractéristiques du saut - durée, hauteur, portée - dépendent notamment de l'inclinaison a de la rampe par rapport au plan horizontal. Dans la partie A, on utilise un moddle simplifié pour prévoir, à partir des équations horaires, comment varient la durée du saut ainsi que la distance et la hauteur maximales théoriques en fonction de l'angle a de la rampe avec l'horizontale. Dans la partie B, on examine la hauteur réellement atteinte à partir des données expérimentales dans le cadre d'une étude énergétique.  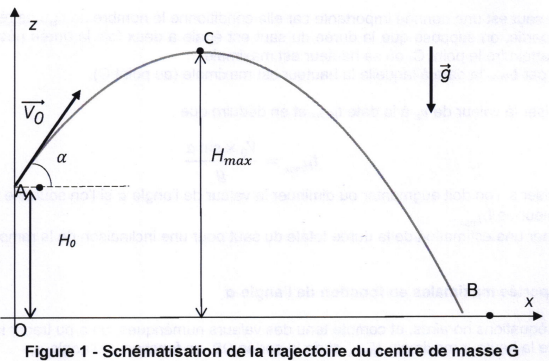On s'intéresse au mouvement du centre de masse G du skieur qui s'élance depuis une rampe, à une hauteur initiale H0, avec une vitesse initiale dont le vecteur est incliné d'un angle a pat rapport à l'horizontale. Dans tout l'exercice, le référentiel terrestre est supposé galiléen. Les axes sont choisis de telle sorte que le plan (Ox, Oz) contienne la trajectoire. Données - Masse du skieur avec son équipement : m = 80 kg - Valeur du champ de pesanteur terrestre g = 9,81 m s-2  - Valeur de la hauteur initiale H0 = 3,60 m - Valeur de Ia vitesse initiale : V0 = 17 m s-1. Partie A - Etude théorique portant sur l'influence de I'angle a entre la rampe et le plan horizontal.  Dans cette partie, on fait les hypothdses simplificatrices suivantes - on néglige les frottements de l'air sur le skieur ; - on néglige les rotations du skieur sur lui-même. La seule force appliquée sur le skieur est donc son poids. 1. Déterminer, à partir de la deuxième loi de Newton, les expressions littérales des coordonnées ax et az du vecteur accélération  du centre de masse G du skieur. Le système n'étant soumis qu'à son poids ( verticale vers le bas, valeur mg ), la seconde loi de newton conduit à : ax =0 ; az = -g.  2. Etablir les expressions des coordonnées vx(t) et vz(t) du vecteur vitesse du centre de masse G et montrer que les équations horaires x(t) et z(t) du centre de masse sont : x(t) = v0 cos a t ; z(t) = -½gt2  +v0 sin a t+H0. La vitesse est une primitive de l'accélération. vx(t) = A ; vz(t) = -gt + B avec A et B des constantes. vx(t=0) = A =v0 cos a ; vz(t=0) = B=v0 sin a . vx(t) =v0 cos a ; vz(t) =-gt+v0 sin a . La position est une primitive de la vitesse. x(t) = v0 cos a t + C ; z(t) = -½gt2  +v0 sin a t+D avec C et D des constantes. x(t=0) = C = 0 ; z(t=0) =D = H0.  Durée du saut en fonction de l'angle a.  La durée du saut est une donnée importante car elle conditionne le nombre de figures réalisables. Dans cette partie, on suppose que la durée du saut est égale à deux fois la durée nécessaire au skieur pour atteindre le point C, où sa hauteur est maximale. On désigne par tHmax, la date à laquelle la hauteur est maximale (au point C).  3. Préciser la valeur de vz à la date tHmax, et en déduire que tHmax = v0 sin a / g. A la date tHmax, vz est nulle :-gtHmax+v0 sin a =0 ; tHmax = v0 sin a / g. 4. Préciser si l'on doit augmenter ou diminuer la valeur de l'angle a si l'on souhaite augmenter la valeur de tHmax. Entre 0 et 90 °, la fonction sinus est croissante ;  pour augmenter tHmax il faut donc faire croître a.  5. Donner une estimation de la durée totale du saut pour une inclinaison de la rampe de 30°. z(t) = -½gt2  +v0 sin a t+H0 = 0. -4,9t2  +17 sin 30 t+3,6 = 0. Discriminant : D =8,52 +4 *3,6 *4,9 =142,81 ~11,952. On retient la racine positive : t =(-8,5 -11,95) / (-2*4,9)=2,08 ~2,1 s. ... .... 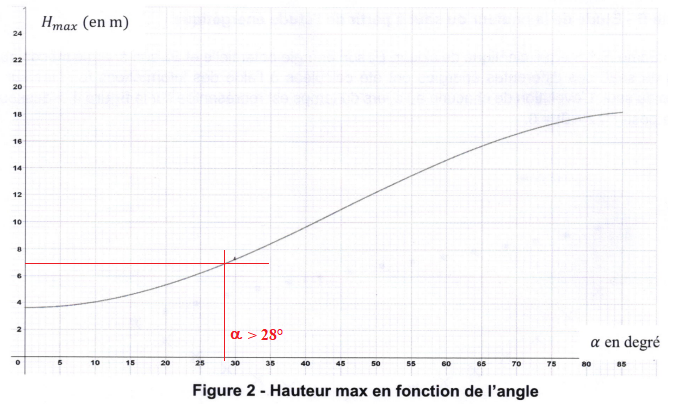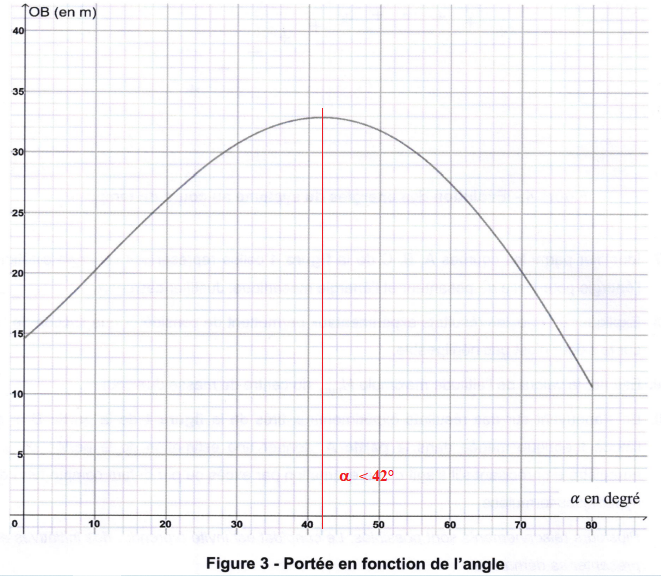Hauteur et portée maximales en fonction de I'angle a.  A partir des équations horaires, et compte tenu des valeurs numériques, on a pu tracer les évolutions de la hauteur maximale Hmax et de la portée OB en fonction de I'angle a. Les graphiques correspondants sont donnés. 6. lndiquer dans quel intervalle de valeurs doit théoriquement se trouver l'angle a pour continuer d'augmenter simultanément la hauteur et la portée tout en permettant d'envisager un saut d'une hauteur d'au moins 7 m. Partie B - Etude de la hauteur du saut à partir de l'étude énergétique.  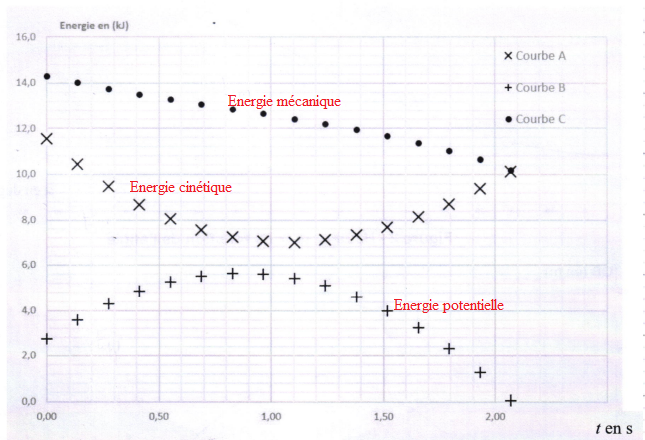On nommeEc I'énergie cinétique du skieur, Ep, son énergie potentielle et Em son énergie mécanique. Lors du saut, ces différentes énergies ont été calculées à I'aide des informations fournies sur la vidéo du saut. L'évolution de chacune au cours du temps est représentée sur la figure ci-dessous. On a posé Ep(z= 0) = 0. 7. ldentifier parmi les courbes A, B, C de la figure celles représentant l'énergie cinétique, l'énergie potentielle de pesanteur et l'énergie mécanique. Justifier ces choix. L'énergie potentielle initiale est égale à m g H0 =80 x9,81 x3,60 =2,8 103 J = 2,8 kJ.. Energie cinétique initiale : 0,5 x 80 x172 =1,16 104 J = 11,6 kJ. Puis elle décroît en passant par le maximum, et croït ensuite. L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. 8. Expliquer en quoi les résultats expérimentaux permettent de considérer que l'action de l'air sur le skieur n'est pas négligeable. L'énergie mécanique n'est pas constante, elle décroît du travail des frottements de l'air.  9. Estimer la valeur de l'altitude maximale Hmax, du centre de masse du skieur. Energie potentielle maximale 5,6 kJ = 5,6 103 J. 5,6 103 = mg Hmax ; Hmax = 5,6 103 /(80 x9,81)=7,1 m.  10. En s'appuyant sur des résultats expérimentaux tirés de la figure ci-dessus et sur l'étude théorique menée dans la partie A, donner une estimation de la portée du saut enregistré en précisant s'il s'agit d'une estimation par excès ou par défaut compte tenu des hypothèses formulées. Hmax est atteinte à t = 0,85 s. x(t) = v0 cos a t avec a = 30°. x =17 cos 30 * 0,85 ~ 13 m, valeur par excès qui ne tient pas compte des frottements.

menu