Probabilités,
fonctions, Mathématiques,
bac général Centres étrangers
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Dans une grande ville française, des
trottinettes électriques sont mises à disposition des
usagers. Une entreprise, chargée de l’entretien du parc de
trottinettes, contrôle leur état
chaque lundi.
Partie A.
On estime que :
- lorsqu’une trottinette est en bon état un lundi, la probabilité
qu’elle soit encore en
bon état le lundi suivant est 0,9 ;
- lorsqu’une trottinette est en mauvais état un lundi, la
probabilité qu’elle soit en bon
état le lundi suivant est 0,4.
On s’intéresse à l’état d’une trottinette lors des phases de
contrôle.
Soit n un entier naturel. On note B n l’événement « la
trottinette est en bon état n semaines
après sa mise en service » et p n la probabilité de B n.
Lors de sa mise en service, la trottinette est en bon état. On a donc p 0
= 1.
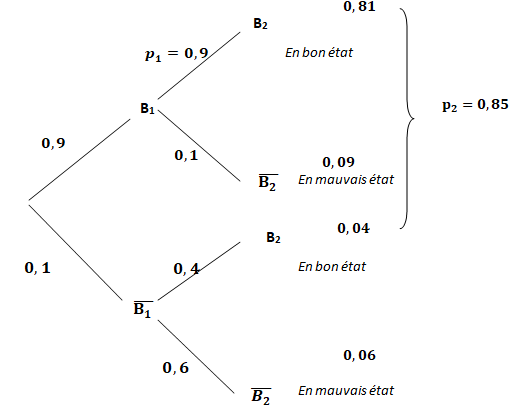
1. Donner p 1
et montrer que p 2 = 0,85. On pourra s’appuyer sur un arbre
pondéré.
 2.
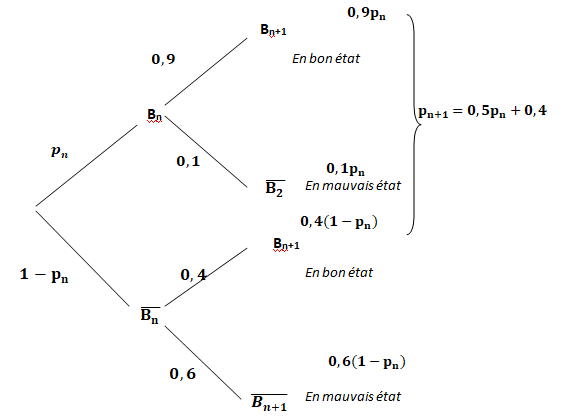
2. Recopier et
compléter l’arbre pondéré ci-dessous.
3. En déduire que,
pour tout entier naturel n, p n+1 = 0,5p n + 0,4.
 4. a.
4. a. Démontrer par
récurrence que pour tout entier naturel n, p n ⩾ 0,8.
Initialisation :
p 1 =0,9, la propriété est vraie au rang 1.
Hérédité
: pn ⩾
0,8 est supposé vrai.
pn+1 = 0,5 pn +0,4 ; pn+1 > 0,5 x0,8
+0,4 ; pn+1 > 0,8. La propriété est
vraie au rang n+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est vraie pour
tout entier n.
b.
À partir de ce résultat, quelle communication l’entreprise peut-elle
envisager pour valoriser la fiabilité du parc ?
La probabilité qu'un e
trotinette soit en bon état à tout moment est supérieure à 0,8.
5.
a. On considère la suite (u n) définie pour tout
entier naturel n par u n = p n − 0,8.
Montrer que (u n) est une suite géométrique dont on donnera
le premier terme
et la raison.
pn+1
= 0,5pn + 0,4 ; un+1 = pn+1 − 0,8= 0,5pn
- 0,4=0,5 (pn
− 0,8)=0,5 un.
u0 =p0-0,8=0,2 ; raison q = 0,5.
b. En
déduire l'expression de u n puis de p n en fonction
de n.
u n =0,2 x0,5 n ; p n = un +0,8 = 0,2 x0,5n +0,8.
c. En déduire la
limite de la suite (p n).
0,5 < 1 ; 0,5n tens vers zéro si n tend vers plus
l'infini ; pn tend vers 0,8.
Partie B.
Dans cette partie, on modélise la situation de la façon suivante :
- l’état d’une trottinette est indépendant de celui des autres ;
- la probabilité qu’une trottinette soit en bon état est égale à 0,8.
On note X la variable aléatoire qui, à un lot de 15 trottinettes,
associe le nombre de
trottinettes en bon état.
Le nombre de trottinettes du parc étant très important, le
prélèvement de 15 trottinettes peut être assimilé à un tirage avec
remise.
1. Justifier que X
suit une loi binomiale et préciser les paramètres de cette loi.
On répète 15 fois et de manière indépendante la même épreuve de
Bernouilli de paramètre p=0,8.
X suit la loi Binomiale de paramètres n = 15 ; p = 0,8.
2. Calculer la
probabilité que les 15 trottinettes soient en bon état.
p(X = 15 = 0,8 15 ~0,035.
3. Calculer la
probabilité qu’au moins 10 trottinettes soient en bon état dans un
lot de 15.
p(X >10) = 1-p(X < 9) =0,939.
4. On admet que E(X) =
12. Interpréter le résultat.
En moyenne, 12 trotinettes sont en bon état sur un lot de 15.
|
...
|
....
|
Une société de production
s’interroge sur l’opportunité de programmer un jeu télévisé. Ce
jeu réunit quatre candidats et se déroule en deux phases.
La première phase est une phase de qualification. Cette phase ne dépend
que du hasard.
Pour chaque candidat, la probabilité de se qualifier est 0,6 .
La deuxième phase est une compétition entre les candidats qualifiés.
Elle n’a lieu que si
deux candidats au moins sont qualifiés. Sa durée dépend du nombre de
candidats qualifiés
comme l’indique le tableau ci-dessous (lorsqu’il n’y a pas de deuxième
phase, on considère
que sa durée est nulle).
Nombre
de canndidats qualifiés pour la deuxième phase
|
0
|
1
|
2
|
3
|
4
|
Durée
de la deuxième phase ( min)
|
0
|
0
|
5
|
9
|
11
|
Pour que la société décide de retenir ce jeu, il faut que les deux
conditions suivantes soient
vérifiées :
Condition n°1 : La deuxième phase doit avoir lieu dans au moins
80% des cas.
Condition n°2 : La durée moyenne de la deuxième phase ne doit pas
excéder 6 minutes.
Le jeu peut-il être retenu ?
On note X la variable aléatoire comptant le nombre de candidats
qualifiés lors de la première phase.
On répète de manière indépendante 4 fois la même épreuve de Bernoulli
de paramètre 0,6.
p(X > 2) =1-p(X =
0)-p(X=1)=1 -0,44 -(4 1)0,61
x0,43 ~0,821.
Cette valeur étant supérieure à 0,8, la première condition est vérifiée.
Durée moyenne : 5 p(X=2) +9P(X=3) +11P(X=4) ~6,3.
Cette valeur étant supérieure à 6, la seconde condition n'est pas
vérifiée. le jeu n'est pas retenu.
Fonction et suite.
On considère la fonction fdéfinie sur ]−1,5 ; +∞[ par f(x) = ln(2x + 3)
− 1.
Le but de cet exercice est d’étudier la convergence de la suite (un)
définie par : u0 = 0 et u𝑛+1 = f(un)
pour tout entier naturel n.
Partie A : Étude d’une
fonction auxiliaire
On considère la fonction g définie sur ]−1,5 ; +∞[ par g(x) = f(x) − x.
1. Déterminer la
limite de la fonction g en −1,5.
Quand x tend vers -1,5 : ln(2x+3) tend vers zéro et f(x)
tend vers moins l'infini
g(x) tend donc vers moins l'infini.
On admet que la limite de la fonction g en +∞ est −∞.
2. Étudier les variations
de la fonction g sur ]−1,5 ; +∞[.
f '(x) = 2 /(2x+3) ; g'(x) = 2 /(2x+3)-1 = (2-2x-3) / (2x+3) =-(2x+1)
/(2x+3).
2x+3 > 0 ; g'(x) a le signe de -(2x+1).
Si x < -0,5, g'(x) > 0 et g(x) est strictement croissante.
Si x > -0,5, g'(x) < 0 et g(x) est strictement décroissante.
Si x = -0,5, g'(x) =0, g(x) présente un maximum.
3. a. Démontrer
que, dans l’intervalle ]−0,5 ; +∞[, l’équation g(x) = 0 admet une
unique
solution a.
g est continue car dérivable sur ]-0,5 ; +oo[.
g(-0,5) = ln(2)-0,5 ~0,19 >0.
En plus l'infini, g(x) tend vers moins l'infini.
D'après le théorèmede la bijection, l'équation g(x) = 0 admet une
solution unique sur ]0,5 ; +oo[.
b. Déterminer un
encadrement de a
d’amplitude 10−2.
La calculatrice donne a
~0,256 : 0,25 < a < 0,26.
Partie B : Étude de la suite (un)
On admet que la fonction f est strictement croissante sur ]−1,5 ; +∞[.
1. Soit x un nombre
réel.
Montrer que si x ∈ [−1; a]
alors f(x) ∈ [−1; a].
g(a) = 0 ; donc f(a)-a =0 ; f(a) = a.
f(-1) = -1.
La fonction f est strictement croissante sur ]-1,5 ; +oo[.
Pour x appartenant à [−1; a],
f(x) apartient à [f(-1) ; f(a)]
soit f(x) ∈ [−1; a].
2. a. Démontrer
par récurrence que pour tout entier naturel n :
−1 ⩽ un ⩽ un+1 ⩽ a.
On note P(n) telle que −1 ⩽ un ⩽ un+1 ⩽ a.
Initialisation
: u0 = 0 ; u1 = f(0)=ln(3)-1 ~0,1.
0 ⩽ u0 ⩽ u1 ⩽ a. la propriété est vraie au
rang zéro.
Hérédité
: −1 ⩽ un ⩽ un+1 ⩽ a est supposé vraie.
La fonction f est strictement croissante sur ]-1,5 ; +oo[, donc f(un)
< f(un+1),
soit un+1 <
un+2.
De plus pour tout x appartenant à [-1 ; a], f(x) appartient à [-1 ; a].
Par suite un+1 et un+2 appartiennent à [-1 ; a].
-1 < un+1
< un+2
< a. Pn+1 est vraie.
Conclusion
: la propriété est vraie au rang zéro et héréditaire, donc elle est
vrai pour tout entier n.
b. En déduire que la
suite (un) converge.
La suite étant croissante et majorée par a, elle converge.
|
|