Plongeon
de haut vol, bac Centres �trangers
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Le
plongeoir est install� � une hauteur de 27 m au dessus de l'eau. le
plongeon est effectu� en 3 s. La vitesse d'impact lors de l'entr�e de
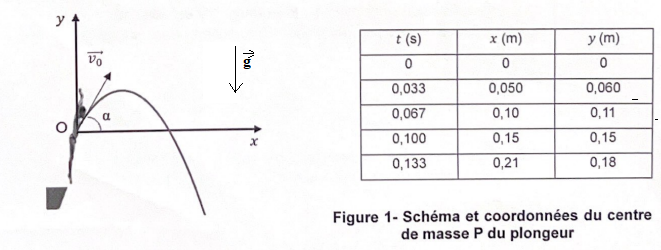
l'eau est proche de 90 km / h. On se concentre sur le centre de masse
du plongeur, not� P. L'origine O du rep�re co�ncide avec la position du centre de masse � t = 0.
Masse du plongeur m = 80 kg.
Etude �nerg�tique.
L'�nergie potentielle de pesanteur est nulle pour y = 0.
1. Compl�ter les lignes 35 et 36 du code Python.
Le
programme permet les repr�sentations graphiques des �volutions au cours
du temps des �nergies cin�tique et potentielle du plongeur durant
quelques millisecondes qui suivent le d�but de la chute.
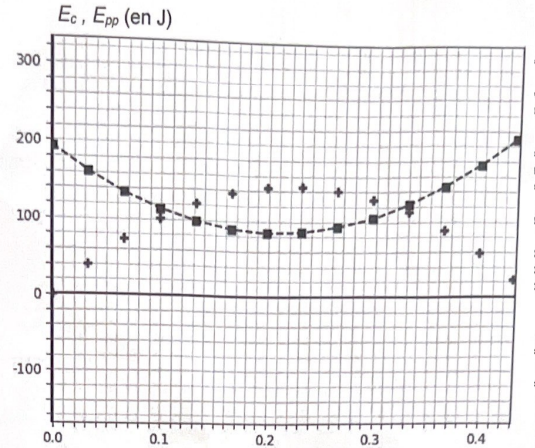2. Justifier que la courbe en pointill�s est celle de l'�volution de l'�nergie cin�tique au cours du temps.
L'�nergie potentielle est nulle � t = 0. L'�nergie cin�tique diminue jusqu'au sommet de la trajectoire puis augmente.
3. Montrer que v0 ~2,3 m /s.
Energie cin�tique initiale =200 = �mv02 = 40v02 ; v02 =5 ; v0=2,23 ~2,3 m /s.
Un autre relev� des coordonn�es du point P, effectu� sur une dur�e plus longue conduit au trac� ci-dessous :
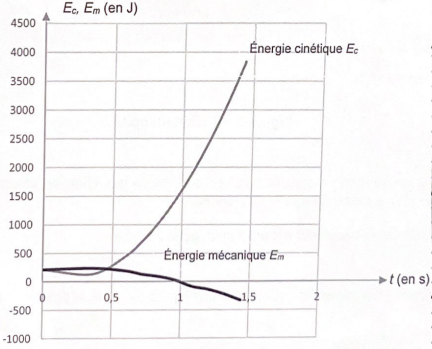
L'�nergie m�canique est constante si t < 0,4 s puis diminue.
4. Pour chaque phase pr�ciser si les frottements sont n�gligeables ou non. Justifier.
t < 0,4 s : frottement n�gligeable et �nergie m�canique constante.
t > 0,4 s : frottement non n�gligeable ; l'�nergie m�canique diminue du travail des frottements.
5.
Formuler une hypoth�se sur l'importance des forces de frottement en
fonction de la vitesse, suivant que celle-ci est faible ou �lev�e.
Aux petites vitesses : l'�nergie m�canique diminue peu et les frottements restent faibles.
Aux vitesses �lev�es : l'�nergie m�canique diminue beaucoup plus et les frottements sont plus importants.
|
...
|
....
|
Etude cin�matique.
6. En utilisant les valeurs du tableau ci-dessus, calculer les coordonn�es v0x et v0y, coordonn�es du vecteur vitesse initiale.
v0x = (0,050-0)/ (0,033-0)=1,515 ~1,5 m /s.
v0y = (0,060-0)/ (0,033-0)=1,818~1,8 m /s.
7. V�rifier que a = 50�.
v0 =(1,5152 +1,8182)�=2,367 m/s.
v0x =v0 cos a ; cos a = 1,515 / 2,367=0,640 ; a~50�.
v0y =v0 sin a ; sin a = 1,818 / 2,367=0,768 ; a~50�.
Dans la suite, on fait l'hypoth�se d'une chute libre. A t = 0 P est � 28 m au dessus de l'eau.
8. Appliquer la seconde loi de Newton au plongeur.
9. Exprimer les coordonn�es du vecteur acc�l�ration et celles du vecteur vitesse.
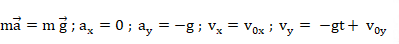
10. En d�duire les �quations horaires du mouvement de P.
La position est une primitive de la vitesse et la position initiale est l'origine du rep�re.
x(t) = v0x t =v0 cos a t.
y(t) = -�gt2 +v0y t = -�gt2 +v0 sin a t .
11. Etablir l'�quation de la trajectoire et montrer qu'elle est compatible avec celle repr�sent�e.
t = x / (v0 cos a ).
Repport dans y(t) : y = -�g x2 / (v0 cos a )2+ tan a x.
Equation d'une parabole, en accord avec le sch�ma.
12. Montrer que la dur�e de la chute est solution de l'�quation : -4,9 t2 +1,8t+28=0.
Au contact avec l'eau y =-28 ; -�gt2 +v0 sin a t =-28.
-4,9 t2 +2,367 x sin 50 t +28 = 0.
-4,9 t2 +1,8t+28=0.
Cette �quation admet deux solutions t1 = -2,21 s et t2 = 2,58 s.
Exp�rimentalement la dur�e de la chute vaut Dt= 2,8 s. La valeur de l'incertitude sur cette dur�e est u(Dt) = 0,3 s.
13. V�rifier que l'hypoth�se de la chute libre est valide.
2,5 < Dt < 3,1 s.
t2 =2,56 s appartient � cet intervalle : l'hypoth�se est valide.
14.15. Montrer que la vitesse lors de l'entr�e dans l'eau est de l'ordre de 24 m /s.
vx=1,515 m /s ; vy=v0y-gt=1,818-9,81 x2,58= -23,5 m/s.
v=(1,5152 +23,52)�=23,54 ~24 m/s ou 23,54 x3,6 ~85 km /h.
Cette valeur est en accord avec 90 km /h du texte ci-dessus.
Une fois dans l'eau, le plongeur s'immobilise en 0,5 s.
16. Estimer la valeur de l'acc�l�ration aeau subie par le plongeur.
|aeau| = |variation de la vitesse| / dur�e = 24 / 0,5 = 48 m s-2 soit environ 5 g.
|
|
