A. Étude du mouvement d’un ballon lors du tir au-dessus du gardien.
Un « jet de 7 mètres » a été reproduit et filmé au gymnase, la chronophotographie du mouvement
du ballon est la suivante :

- hauteur de la barre transversale d’un but de handball : 2,0 m.
Dans cette étude :
- Le système étudié est le ballon, les coordonnées de la position de son centre de masse G
sont notées (x ; y) dans le repère.
- Dans ce repère, les coordonnées du vecteur vitesse du ballon sont notées (v
x ; v
y) et celles
de son vecteur accélération sont notées (a
x ; a
y).
- Le vecteur vitesse initiale v
0 du ballon forme un angle
a avec l’horizontale.
- L’action de l’air sur le ballon est négligée.
- L’instant t = 0 correspondant à l’origine des dates est choisi juste après que le ballon a quitté
la main du tireur.
À cet instant, les coordonnées du centre de masse G du ballon sont (x
0 = 0 ;
y
0 = h = 2,34 m)
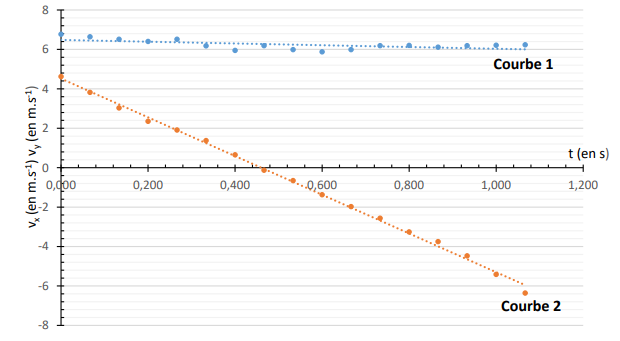
- Les courbes représentant les coordonnées du vecteur vitesse au cours du temps, après
étalonnage du repère et pointage des positions successives du centre du ballon, sont
données ci-dessous :
 Q.1.
Q.1. Nommer le référentiel dans lequel la trajectoire du ballon est observée sur la
chronophotographie.
Référentiel terrestre.
Q.2. En précisant certaines hypothèses, établir l’expression du vecteur accélération du
centre de masse du ballon lors du tir. Établir les coordonnées de ce vecteur dans le
repère R.
L'action de l'air étant négligée, la ballon n'est soumis qu'à son poids.
La seconde loi de Newton conduit à : a
x = 0; a
y = -g.
Q.3. Parmi les expressions proposées pour l’intensité du champ de pesanteur terrestre,
déterminer par analyse dimensionnelle celle qui est homogène (on note M la masse de la
Terre et R son rayon) :
a) g =
G·M
2/ R ;
b) g =
G·M/
R2 vrai ; c) g =
(G+M) / R
2..
G s'exprime en m
3 kg
-1s
-2 ; M s'exprime en kg et R en mètre :
G·M2/ R s'exprime en m4kg s-2 ;
G·M/
R2 s'exprime en m s-2 , dimension d'une accélération.
c) G et M ne s'additionnent pas.
Q.4. Montrer que les expressions des coordonnées du vecteur vitesse du centre de masse
du ballon lors du tir sont :
v
x
(t) = v
0
· cos (
a) ; v
y
(t) = -g·t +
v0
· sin (a).
La vitesse est une primitive de l'accélération :
vx
(t) =A ; vy
(t) = -g·t + B. A et B sont des constantes.
vx
(t=0) =A = v0
· cos (a) ; vy
(t=0) = B= v0
· sin (a).
Q.5. Sur le graphique représentant l’évolution des coordonnées du vecteur vitesse au cours
du temps, identifier la courbe correspondant à v
x et celle correspondant à v
y. Justifier.
v
x(t) est constant : courbe 1 ;
v
y décroît au cours du temps, s'annule en passant au sommet de la trajectoire puis change de signe ( courbe 2).
Q.6. Calculer à partir de ces courbes la norme v
0 du vecteur vitesse initiale, ainsi que la
valeur de l’angle
a.
v0
· cos (a) =6,4 m /s ; v0
· sin (a) =4,6 m /s ;
tan (a) =4,6 / 6,8 ~0,676 ; a ~34°.
v0 =4,6 / sin (a) =8,2 m /s ;
Q.7. Établir les équations horaires x(t) et y(t) du mouvement lors du tir.
La position est une primitive de la vitesse.
x (t) = v0
· cos (a) t + C ; y
(t) = -½g·t2 + v0
· sin (a) t + D avec C et d des constantes.
x (t=0) =0= C ; y
(t=0) =h= D = 2,34 m.
x (t) = v0
· cos (a) t ; y
(t) = -½g·t2 + v0
· sin (a) t + h.
Q.8. En déduire que l’équation y(x) de la trajectoire s’écrit :
y(x) = -
½·g·
x
2
/ (v
0 2 ·cos
2(
a) )+ tan (a
)·x + h.
t =
x (t) /( v0
· cos (a)), repport dans y(t) :
y
(x) = -½g·x2 / (v0 2 ·cos 2(a) ) + x
· tan (a) + h.
Q.9. Le gardien étant situé à 4,0 m du tireur, déterminer si le « jet de 7 mètres » étudié
permet de marquer un but. On considère que le gardien peut atteindre avec son bras levé
une hauteur maximale de 2,8 m en plein saut.
y
(4) = -0,5 x 9,81x42 / (8,2 2 ·cos 2(34) ) +4 x
· tan (34) + 2,34 = 3,3 m > 2,8 m.
Le ballon passe au dessus du gardien.