A la d�couverte de Saturne, bac g�n�ral m�tropole 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. . . . . . . .. .. ...... ... Le but de cet exercice est d’�tudier la lunette astronomique de Huygens afin de comparer ses observations de Saturne et de ses anneaux � celles de Galil�e. La fin de l’exercice est consacr�e � l’�tude du mouvement du satellite Titan � partir des observations de Huygens. 1. Observation de Saturne par Huygens  La lunette de Huygens, consid�r�e comme afocale, est mod�lis�e par un syst�me de deux lentilles minces convergentes not�es L1 et L2. La lentille L1 repr�sente l’objectif et la lentille L2 l’oculaire. 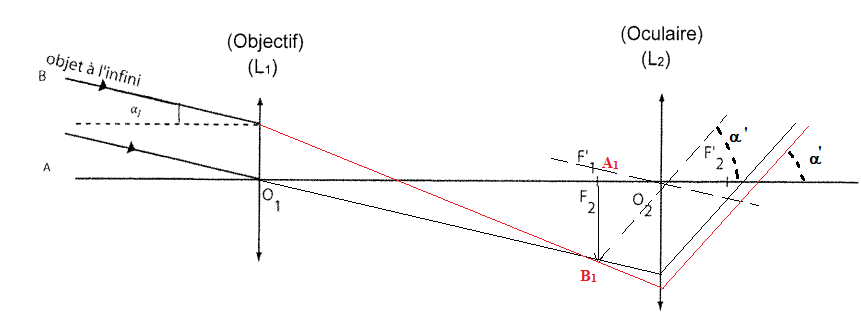Leurs centres optiques respectifs sont not�s O1 et O2 et leurs distances focales respectives sont not�es f1' et f2'. La lunette est utilis�e pour observer un objet AB, suppos� � � l’infini �, dont l’image par l’objectif sera not�e A1B1. Deux rayons lumineux issus de B sont repr�sent�s sur le sch�ma. Q1. Pr�ciser le sens du terme � afocal �. La lunette est afocale car elle donne d'un objet situ�e � l'infini, une image situ�e � l'infini. Des rayons parall�les entre eux avant le syst�me optique, ressortent parall�les apr�s le syst�me. Q2. Placer, sur la figure les foyers objet F2 et image F’2 de la lentille L2 dans le cas d’une lunette afocale.  Q3. Construire, sur la figure la marche des deux rayons lumineux issus de B qui �mergent de la lunette en faisant appara�tre l’image interm�diaire A1B1. 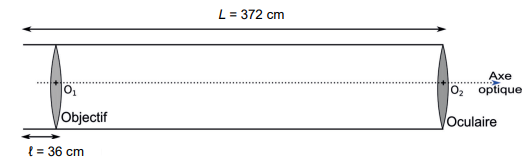La lunette de Huygens est constitu�e d’un tube long de 372 cm. L’oculaire est plac� � une extr�mit� du tube. L’objectif quant � lui est enfonc� de 36 cm par rapport � l’autre extr�mit�, afin de le prot�ger de la bu�e. Q4. V�rifier, � partir des donn�es, que la lunette d’Huygens peut �tre consid�r�e comme � afocale �. Donn�es : f '1 = 329 cm ; f '2 = 7,0 cm. O1O2 =372 -36= 336 cm. O1O2 =f '1 +f '2.  L’angle a, repr�sent� sur la figure d�signe l’angle sous lequel l’espace AB entre la surface de Saturne et son premier anneau est vu � l’œil nu depuis la Terre, lorsque les anneaux de Saturne sont vus de face. On note a’ l’angle sous lequel un observateur voit l’image A’B’ de l’espace AB, � travers la lunette astronomique.  Q5. Placer l’angle a’ sur la figure.  Q6. Donner l’expression du grossissement GHuy de la lunette de Huygens en fonction des angles a et a’. GHuy = a' / a.  Q7. Montrer que le grossissement GHuy de la lunette de Huygens s’exprime en fonction des distances focales des lentilles L1 et L2 constituant la lunette : GHuy= f1' f2' . Triangle O1A1B1 : tan a ~ a =A1B1 / f '1. Triangle O2A1B1 : tan a' ~ a' =A1B1 / f '2 Par suite GHuy = a' / a.= f '1 / f '2. Q8. Calculer la valeur du grossissement GHuy de la lunette utilis�e par Huygens.  GHuy=329 / 7,0 =47. Q9. Conclure sur la possibilit� pour Huygens de distinguer la surface de Saturne de son premier anneau en utilisant la lunette. La distance entre la surface de Saturne et son premier anneau est �gale �  DA-B = 3,17 104 km. Distance Terre-Saturne : DT-S = 1,42�109 km. a ~DA-B / DT-S =3,17 104 / (1,42 109)=2,23 10-5 rad. a' = 2,23 10-5 x47=1,0 10-3 rad. Cette valeur �tant sup�rieure � 3,0 10-4 rad, Huygens  peut distinguer la surface de Saturne de son premier anneau en utilisant la lunette. 2. Prise en compte de la diffraction dans l’observation astronomique.  L’observation des d�tails d’un objet avec une lunette astronomique est principalement limit�e par le ph�nom�ne de diffraction. En effet, l’image donn�e par l’objectif d’une source ponctuelle � � l’infini � n’est pas un point mais une figure de diffraction circulaire, appel�e tache d’Airy. 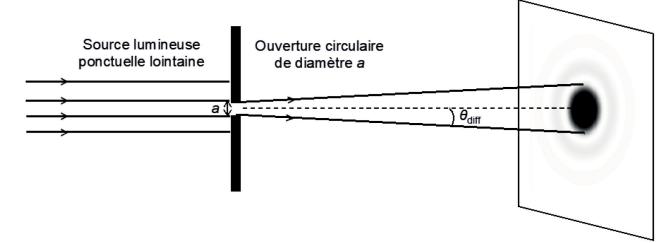Dans le cas de la lunette astronomique, on admet que l’angle caract�ristique de diffraction v�rifie la relation :  qdiff = 1,22 � λ / a avec l la longueur d’onde du faisceau incident et a le diam�tre de l’objectif. Une lunette astronomique ne permet de distinguer deux points A et B que si l’�cart angulaire q entre les directions de ces deux points vus depuis la Terre est sup�rieur ou �gal � l’angle caract�ristique de diffraction, c’est-�-dire si la condition q ≥ qdiff est v�rifi�e. Si ce n’est pas le cas, les taches d’Airy associ�es aux deux points se superposent et les deux points ne peuvent �tre s�par�s visuellement. Q10. Expliquer pourquoi on peut consid�rer que le ph�nom�ne de diffraction a emp�ch� Galil�e d’observer les anneaux de Saturne avec sa lunette astronomique contrairement � Huygens qui a pu les observer.  Une approche quantitative est attendue. On rappelle que la distance entre Saturne et la limite du premier anneau visible � l’�poque est �gale � DA-B = 3,17�104 km et on effectuera les calculs avec une valeur de la longueur d’onde l = 550 nm, pour laquelle l’œil humain est le plus sensible. Grossissement de la lunette de Galil�e : GGal = 14. Diam�tre de son objectif 29,0 mm. q = 2,23 10-5  rad.  qdiff = 1,22 �550 10-9 / (29 10-3)=2,3 10-5 rad. q < qdiff Galil�e ne peut pas observer les anneaux. Grossissement de la lunette de Huygens : GHuy = 47. Diam�tre de son objectif 51,0 mm. q = 2,23 10-5 rad.  qdiff = 1,22 �550 10-9 / (51 10-3)=1,3 10-5 rad. q > qdiff Huygens peut observer les anneaux. ... .... 3. D�couverte de Titan par Huygens.  Le 25 mars 1655, � 8 heures du soir, employant sa lunette, Huygens aper�oit pr�s de Saturne, un point brillant qu'il soup�onne �tre un satellite de cette plan�te. Plus tard, ce satellite sera appel� Titan. � Apr�s le 25 mars 1655, � savoir le 10 avril, le satellite a �t� vu � la m�me position qu'il occupait � cette premi�re date. De m�me, le 3 et le 19 avril de cette m�me ann�e des positions identiques furent observ�es ; de m�me encore le 13 et le 29 de ce mois. Tenant donc compte de ces r�sultats, j'ai dessin� une circonf�rence de cercle repr�sentant l'orbite du satellite, avec Saturne au centre, et je l'ai divis�e en 16 parties, comme le montre la figure suivante. Dans cette orbite j'ai fait circuler le satellite suivant l'ordre naturel des chiffres. […] Q11. Justifier le choix de Huygens de diviser la trajectoire de Titan en 16 parties. Du 25 mars au 10 avril, il y a 16 jours ; de m�me du 3 au 19 avril ; de m�me du 13 au 29 avril. Le satellite a �t� vu � la m�me position qu'il occupait � cette premi�re date. Le mouvement de Titan, not� T, est �tudi� dans le r�f�rentiel saturnocentrique, dont l’origine est plac�e au centre S de Saturne et dont les axes sont dirig�s vers des �toiles lointaines. Il est consid�r� comme galil�en. On travaille dans le rep�re de Frenet . Dans Systema Saturnium, Huygens pr�cise que la valeur de la p�riode de r�volution THuy de Titan est de � 15 jours 23 heures 13 minutes �. Masse de Saturne M ; masse de Titan : m ; rayon de l'orbite de Titan : r.  Q12. Donner l’expression vectorielle de la force d’interaction gravitationnelle exerc�e par Saturne sur le satellite Titan en fonction de G, M, m, r et de l’un des vecteurs unitaires. Q13. Le mouvement de Titan autour de S est suppos� circulaire. Montrer qu’il est uniforme puis que l’expression de la vitesse du satellite s’�crit sous la forme : v = (GM / r)�. La norme de la vitesse �tant constante, le mouvement est uniforme. Q14. En d�duire l’expression de la p�riode de r�volution not�e T de Titan. Calculer sa valeur. Commenter. Titan d�crit une circonf�rence de rayon r en T seconde � la vitesse v (m/s). 2pr = vT ; v = 2pr  / T ; v2 =4 p2r2 / T2 = GM / r. T2=4p2r3/ (GM). M =5,68 1026 kg ; r = 1,22 109 m. T2=4 x3,142 x(1,22 109)3 / (6,67 10-11 x 5,68 1026 )=1,9 1012 ; T =1,4 106 s ou environ 16 jours, en accord avec les observations.

menu