Forces aérodynamiques sur un volant de badminton, bac général métropole 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . .. . . . . .. .. ...... ... On s’intéresse au mouvement d’un volant de badminton lancé, à la date t = 0,0 s d’un point noté G0 avec une vitesse initiale v0 = 40 m·s-1, et faisant un angle q0 = 60° avec l’horizontale. La chronophotographie de ce mouvement est donnée ci-dessous. L’axe des x est suivant l’horizontale et l’axe des y suivant la verticale ascendante. le volant étudié est de modèle MAVIS 370 de longueur L = 60 mm et un rayon R = 34 mm. La masse de ce volant est m = 5,3 g dont 3 g sont répartis dans le bouchon et 2,3 g dans la jupe. 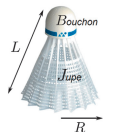On étudie la trajectoire du centre de masse du volant de badminton. Q1. Estimer à l’aide d’une mesure graphique la valeur de la vitesse du volant à la date t = 0,160 s, c’est-à-dire la vitesse au point G4. Q2. Représenter cette vitesse sur la chronophotographie  en utilisant une échelle de 1,0 cm pour 5,0 m·s-1. v4 = G3G5 / (2Dt) = 1,5 / 0,08=18,75 ~19 m /s. On suppose dans un premier temps que l’action de l’air est négligeable devant le poids du volant. Les résultats obtenus dans le cadre de cette hypothèse seront ensuite comparés avec les résultats expérimentaux afin de déterminer s’il est nécessaire de prendre en compte cette action pour modéliser de manière pertinente le mouvement du volant de badminton.  Q3. En appliquant la deuxième loi de Newton au volant lancé, à l’instant t = 0,0 s, avec une vitesse initiale v0 faisant un angle q0 avec l’horizontale, montrer que les équations horaires des coordonnées vx et vy de son vecteur vitesse s’écrivent :  vx = v0 × cos(q0) et vy = - g × t + v0 × sin(q0). Le système n'est soumis qu'à son poids. La seconde loi de Newton conduit à : ax = 0 et ay = -g. La vitesse est une primitive de l'accélération : vx = cste = v0 × cos(q0). vy= -gt + cste  ; vy(t=0) = Cste = v0 × sin(q0) vy = - g × t + v0 × sin(q0).  Q4. Déterminer les valeurs des coordonnées vx et vy de la vitesse à la date t = 0,160 s.  vx = 40 × cos( 60)=20 m /s. vy = -9,81x0,160 + 40 sin(60) =33,1 m /s. Q5. En déduire, dans le cadre de ce modèle, la valeur de la vitesse à cette date. Commenter en la comparant à celle déterminée à la question Q1. v = [vy2 +vx2]½ = [33,12 +202]½ =38,7 m /s. Cette valeur est 2 fois supérieure à celle trouvée question 1. Parmi les forces à prendre en compte dans l’étude de ce mouvement, il existe une action modélisée par une force appelée force de trainée. La force de trainée peut être modélisée par l’expression F=kv2, de sens contraire à la vitesse où k = 1,4×10-3 kg·m-1 est une constante dépendant entre autre de la masse volumique de l’air et de la dimension du projectile, v la norme du vecteur vitesse. Q6. Représenter sans souci d’échelle le vecteur force de trainée au point G1 . 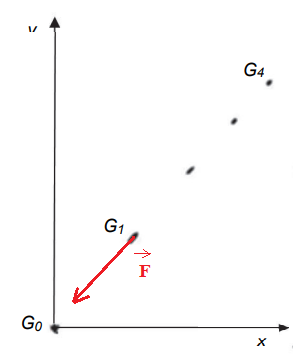Q7. Montrer quantitativement que, pour une vitesse de valeur v0 = 40 m·s-1 du volant, la force de trainée ne peut pas être négligée devant le poids. P = mg = 5,3 10-3 x9,81=0,052 N. F = 1,4 10-3 x402 =2,24 N très supérieur à la valeur du poids.   ... .... Le graphique ci-dessous représente les trajectoires d’un volant en plume et d’un volant en plastique lancés dans les mêmes conditions. Q8. Analyser qualitativement ce graphique et formuler une hypothèse concernant la valeur de la force de trainée qui s’exerce sur un volant en plastique par rapport à celle qui s’exerce sur un volant en plume. Le volant en plume retombe plus rapidement au sol. La force de trainée est plus importante que dans le cas du volant en plastique.

menu