Sécurité d’un four à pyrolyse.
Certains fours électriques possèdent un mode appelé pyrolyse qui facilite leur
nettoyage. On peut lire dans une notice de constructeur :
« Durant l'opération de nettoyage par pyrolyse, la température du four peut monter
jusqu'à 500°C. Pour votre sécurité, la porte du four se verrouille automatiquement
pendant l'opération de nettoyage et le voyant “verrou” s'allume. Lorsque le four aura
suffisamment refroidi, le système se déverrouillera et permettra à nouveau l'ouverture
de la porte. »
Données :
− Masse du four : 35 kg
− Température de la pièce : 20°C.
Capacité thermique massique du four.
Durant la montée en température, la consommation électrique du four est de 2,6 kWh.
On suppose que cette énergie électrique est entièrement utilisée par la résistance
chauffante du four pour le porter jusqu’à 500°C.
1. Nommer l’effet thermique se produisant dans la résistance.
Effet Joule.
2. Convertir cette consommation électrique en joule.
2,6 x3,6 10
6 =9,36 10
6 J.
3. Calculer la capacité thermique massique du four.
Q =m C (T
fin - T
ini) ; C = Q / [ m
(Tfin - Tini)]=
9,36 106 /(35 x(500-20))~5,6 102 J kg-1K-1.
La capacité thermique massique ainsi calculée intervient dans la modélisation de la
phase de refroidissement du four.
Modélisation de la phase de refroidissement.
La fonction
q, représentée ci-dessous, modélise l’évolution de la température du four
(exprimée en degré Celsius) en fonction du temps t (exprimé en minute) écoulé depuis
la fin de la pyrolyse. L’instant initial t = 0 correspond au début de la phase de
refroidissement.
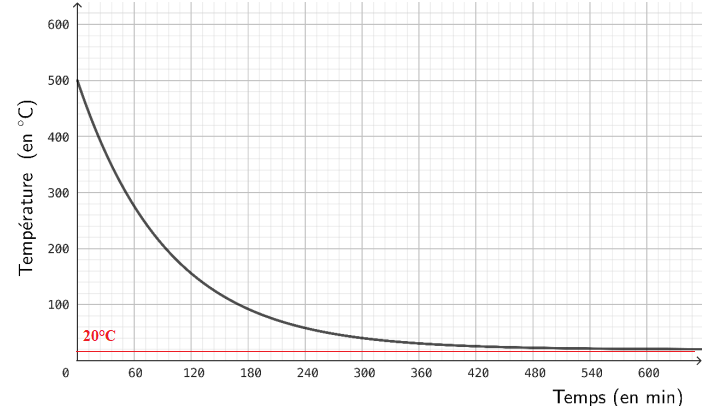 4.
4. Déterminer graphiquement la limite de
q(t) en plus l'infini.
5. Interpréter cette limite dans le contexte de l’exercice.
Le four se trouve à la température de la pièce.
La fonction
q utilisée pour cette modélisation est définie sur [0 ; +∞[ par :
q(t) = 480 exp(
− t / 95) + 20.
6. Calculer la valeur exacte de la solution de l’équation
q(𝑡) = 280.
280= 480 exp(
− t / 95) + 20.
260 / 480 = exp(
− t / 95) ; 13 / 24 =exp(
− t / 95) ;
ln(13 / 24) = -t / 95 ; ln(24 / 13) = t / 95 ; t = 95 ln(24 / 13) ~ 58 minutes.
Pour des raisons de sécurité, le fabricant impose que la porte du four reste verrouillée
tant que la température du four est supérieure à 280°C.
7. Au bout de combien de temps la porte se déverrouille-t-elle ?
t = 95 ln(24 / 13) ~ 58 minutes.
Une mesure originale de température.
Le robot Persévérance a pour mission de ramasser des échantillons de roches
martiennes. Un rayonnement laser infrarouge est émis à intervalles de temps réguliers
et casse les roches à collecter. Les roches émettent alors un son qui est capté par les
microphones du robot.
Lors de l’analyse des enregistrements audio, les scientifiques ont mis en évidence des
variations de température inattendues. Cette découverte repose sur la mesure de la
vitesse de propagation des ondes sonores dépendante de la température.
Cet exercice propose de comprendre le principe de la mesure de la température à la
surface de Mars en s’appuyant sur des expériences effectuées sur Terre.
Un schéma possible de l’expérience martienne est le suivant
1. Expliciter ce que représentent P, R et d dans ce contexte.
2. Indiquer les lieux d’émission et de réception des ondes sonores sur le schéma.
 3.
3. Proposer une liste de matériel nécessaire pour vérifier expérimentalement au
laboratoire l’affirmation : « la vitesse de propagation des ondes sonores dépend
de la température ».
Emetteur récepteur à ultrasons ; oscilloscope ; système de chauffage ; thermomètre.
L’expérience de mesure de la vitesse de propagation du son dans l’air est conduite
avec un émetteur et un récepteur à ultrasons. Elle a été reproduite en trois lieux
différents d’un lycée : le laboratoire de physique, la chambre froide et le congélateur
des cuisines. La distance entre l’émetteur et le récepteur est restée la même pour les
trois expériences : 1,80 m.
Lieu
|
température °C
|
durée Dt de la propagation du son entre émetteur et récepteur (ms)
|
vson dans l'air ( m /s)
|
laboratoire
|
24,2
|
5,21
|
|
chambre froide
|
9,0
|
5,38
|
335
|
congélateur
|
-10,8
|
5,56
|
324
|
4. Déterminer la valeur expérimentale de la vitesse du son sur Terre à 24,2°C.
v = d /
Dt =1,80 / (5,21 10
-3)=3,45 10
2 m /s.
Lors de la collecte des échantillons de roches martiennes, le laser et le microphone
sont synchronisés avec une précision de ± 0,01 ms sur la mesure de la durée de
propagation du son.
5. Vérifier que la précision des valeurs mesurées sur Terre est du même ordre de
grandeur que la précision des mesures martiennes.
Les durés sont données avec 3 chiffres significatifs. La précision est donc ±0,01 ms.
Dans l’hypothèse où l’atmosphère est assimilée à un gaz parfait, la température est
proportionnelle au carré de la vitesse de propagation : T = a v
son2 ; v
son est exprimée en m s
−1
; la température absolue T est exprimée en kelvin K ;
a= 2,49 × 10
−3 u ⋅ s ⋅ i.
6. Calculer la température absolue du congélateur en exploitant la relation
précédente.
T =2,49 10
-3 x324
2 =261,4 ~261 K.
7. Convertir en kelvin la température du congélateur mesurée directement avec le
thermomètre.
273 -10,8 =262,2 ~262 K.
8. Comparer les deux mesures et conclure sur la précision de la technique
employée par les scientifiques pour mesurer la température à la surface de Mars.
Ecart relatif : (262,2 -261,4) / 262 x100 =0,3 %.
La mesure de la température reposant sur la mesure de la
vitesse de propagation des ondes sonores est plus précise à toute température.