Probabilités,
Bac Amérique du sud 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
1.
Entre 1998 et 2020, en France 18 221 965
accouchements ont été recensés, parmi lesquels
293 898 ont donné naissance à des jumeaux et 4 921 ont donné naissance
à au moins trois enfants.
a. Avec une
précision de 0,1% calculer parmi tous les accouchements recensés, le
pourcentage d’accouchements donnant naissance à des jumeaux sur la
période 1998-2020.
293 898 / 18 221 965 x100=1,61 %.
b. Vérifier que le
pourcentage d’accouchements qui ont donné naissance à au moins trois
enfants est inférieur à 0,1%.
On considère alors que ce pourcentage est négligeable.
4921 / 18 221 965 x100=0,027 %.
On appelle
accouchement ordinaire, un accouchement donnant naissance à un seul
enfant.
On appelle accouchement double, un accouchement donnant naissance à
exactement deux enfants.
On considère dans la suite de l’exercice qu’un accouchement est soit
ordinaire, soit double.
La probabilité d’un accouchement ordinaire est égale à 0,984 et celle
d’un accouchement double est alors égale à 0,016.
Les probabilités calculées dans la suite seront arrondies au millième.
2. On admet qu’un
jour donné dans une maternité, on réalise n accouchements.
On considère que ces n accouchements sont indépendants les uns des
autres.
On note X la variable aléatoire qui donne le nombre d’accouchements
doubles pratiqués ce jour.
a. Dans le cas où n
= 20, préciser la loi de probabilité suivie par la variable aléatoire X
et calculer la probabilité qu’on réalise exactement un accouchement
double.
Les acouchements sont des événements indépendants ; la probabilité
d'avoir une naissance est égale à 0,016. X suit la loi binomiale
de paramètres n = 20 ; p = 0,016.
P(X =1) = 20 x0,016 x(1-0,016)19 ~0,236.
b. Par la méthode
de votre choix que vous expliciterez, déterminer la plus petite valeur
de n telle que p(X >1)>0,99.
Interpréter le résultat dans le contexte de l’exercice.
p(X >1)=1-
p(X=0) =1-0,984n x0,0160 = 1-0,984n > 0,99.
0,01 > 0,984n
; ln (0,01) > n
ln(0,984) ; n >
ln(0,01) / ln(0,984) ; n >
286.
Sur 286 accouchement, il y a en moyenne un accouchement double.
3. Dans cette maternité, parmi les
naissances double, on estime qu’il y a 30%de jumeaux monozygotes
(appelés « vrais jumeaux » qui sont obligatoirement de même sexe : deux
garçons ou deux filles) et donc 70% de jumeaux dizygotes (appelés «
faux jumeaux », qui peuvent être de sexes différents : deux garçons,
deux filles ou un garçon et une fille).
Dans le cas de naissances doubles, on admet que, comme pour les
naissances ordinaires, la probabilité d’être une fille à la naissance
est égale à 0,49 et que celle d’être un garçon à la naissance est égale
à 0,51.
Dans le cas d’une naissance double de jumeaux dizygotes, on admet aussi
que le sexe du second nouveau-né des jumeaux est indépendant du sexe du
premier nouveau-né.
On choisit au hasard un accouchement double réalisé dans cette
maternité et on considère les évènements suivants :
• M : « les jumeaux sont monozygotes »;
• F1 : « le premier nouveau-né est une fille »;
• F2 : « le second nouveau-né est une fille ».
a. Recopier puis
compléter l’arbre pondéré ci-dessous.
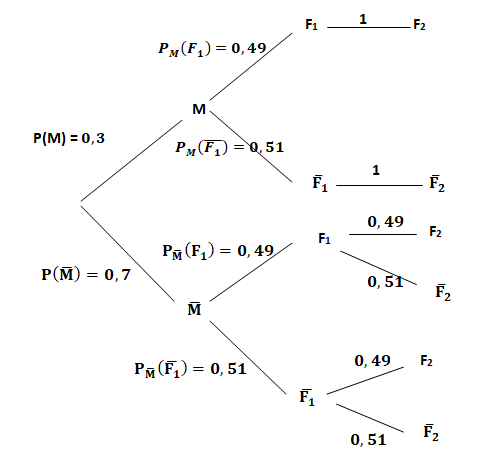
b. Montrer que la
probabilité que les deux nouveaux-nés soient des filles est 0,315 07.
Première branche et troisième branche de l'arbre :
p(F1 n F2) =0,3 x1 x0,49 + 0,7 x 0,49 x0,49 = 0,315 07.
c. Les deux nouveaux-nés sont des
jumelles. Calculer la probabilité qu’elles soient monozygotes.
p F1 n F2(M) =p(M n (F1 nF2)) / p(F1
n F2) =0,3 x1 x0,49 / 0,315 07~0,467.
|
...
|
....
|
Partie A
Un jeu proposé dans une fête foraine consiste à effectuer trois tirs
successivement sur une cible mouvante.
On a constaté que :
• Si le joueur atteint la cible lors d’un tir alors il ne l’atteint pas
lors du tir suivant dans 65% des cas;
• Si le joueur n’atteint pas la cible lors d’un tir alors il l’atteint
lors du tir suivant dans 50% des cas.
La probabilité qu’un joueur atteigne la cible lors de son premier tir
est de 0,6.
On choisit au hasard un joueur à ce jeu de tirs.
On considère les évènements suivants :
• A1 : « Le joueur atteint la cible lors du 1er tir »
• A2 : « Le joueur atteint la cible lors du 2e tir »
• A3 : « Le joueur atteint la cible lors du 3e tir ».
1. Recopier et
compléter, avec les probabilités correspondantes sur chaque branche,
l’arbre pondéré ci-dessous modélisant la situation.
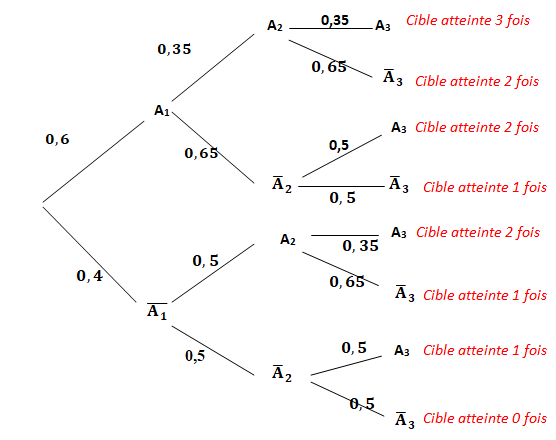
Soit X la variable aléatoire qui donne le nombre de fois où le joueur
atteint sa cible au cours des trois tirs.
2. Montrer que la
probabilité que le joueur atteigne exactement deux fois la cible au
cours des trois tirs est égale à 0,401 5.
0,6 x0,35 x0,65 +0,6 x0,65 x0,5 +0,4 x0,5 x0,35 =0,1365 +0,195
+0,07=0,401 5.
3. L’objectif de
cette question est de calculer l’espérance de la variable aléatoire X,
notée E(X).
a. Recopier et
compléter le tableau ci-dessous donnant la loi de probabilité de la
variable aléatoire X.
X
= xi
|
0
|
1
|
2
|
3
|
p(X
= xi)
|
0,1
|
1-0,1-0,401
5-0,0735=0,425
|
0,401 5
|
0,0735
|
b. Calculer E(X).
E(X) = 0,425 +2 x0,4015 +3 x0,0735 =1,4485.
c. Interpréter le
résultat précédent dans le contexte de l’exercice.
Sur trois tirs, la cible est atteinte 1,5 fois.
Partie B.
On considère N, un entier naturel supérieur ou égal à 1.
Un groupe de N personnes se présente à ce stand pour jouer à ce jeu
dans des conditions identiques et indépendantes.
Un joueur est déclaré gagnant lorsqu’il atteint trois fois la cible.
On note Y la variable aléatoire qui compte parmi les N personnes le
nombre de joueurs déclarés gagnants.
1. Dans cette
question, N =15.
a. Justifier que Y
suit une loi binomiale dont on déterminera les paramètres.
On effectue 15 expériences identiques et indépendantes. Y suit la loi
binomiale de paramètres n = 15 ; p = 0,0735.
b. Donner la
probabilité, arrondie à 10−3, qu’exactement 5 joueurs soient
gagnants à ce jeu.
p(Y = 5) =(15 5) x0,07355 x(1-0,0735)15-5
~0,003.
2. Par laméthode de
votre choix, que vous expliciterez, déterminer le nombre minimum de
personnes qui doivent se présenter à ce stand pour que la probabilité
qu’il y ait au moins un joueur gagnant soit supérieure ou égale à 0,98.
p(Y >1) > 0,98.
1-p(Y=0) > 0,98 ;
0,02 > p(Y =0)
0,02 >(n
0) x0,07350 x(1-0,0735)1n
;
0,02 >0,9265n
; ln(0,02) > n
ln(0,9265)
n < ln(0,02) /
ln(0,9265) ; n >
52.
|
|