Mathématiques, concours Police Technique et Scientifique 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

. .
.. ..
......


...
Question 1 : (2 points)
On suppose a réel strictement négatif : la fonction f(x) = 1 / (1 + a e-x) est
A. définie sur R
B. n’est pas définie en x=−ln(−a)
C. n’est pas définie en x=−ln(1/a) Vrai
D. n’est pas définie en x=ln(−a)
Le dénominateur doit être différent de zéro.
e-x > 0 ; a e-x < 0 ;  e-x doit être différent de -1 / a.
-x doit être différent de ln(-1 /a) ; x doit être différent de ln(a).

Question 2 : (2 points)
On suppose a strictement négatif : le nombre de droites asymptotes à la courbe représentative de f est
A. 1
B. 2
C. 3
D. 0.

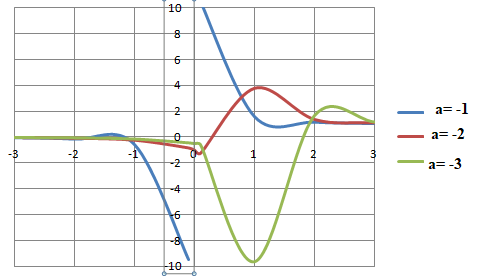Si a diffère de -1: quand x tend vers plus l'infini; e-x tend vers zéro et f(x) tend vers 1. La droite d'équation y = 1 est asymptote.
Quand x tend vers moins l'infini; e-x tend vers plus l'infini et f(x) tend vers 0. La droite d'équation y = 0 est asymptote.
Si a = -1 : en plus des asymptotes précédentes, la droite d'équation x = 0 est asymptote.

Question 3 : (2 points)
On suppose a strictement positif :
A. La fonction f est décroissante sur R
B. La fonction f est croissante sur R. Vrai.
C. La fonction f n’est pas monotone sur R
D. La fonction f prend des valeurs négatives sur R.
f '(x)= ae-x /(1+ae-x)2 < 0 ; f(x) est strictement croissante sur R allant de zéro à 1.

Question 4 : (2 points)
La fonction f est solution de l’équation différentielle
A. y ’= y (1−y ) vrai.
B. y ’= y (1+ y)
C. y ’=−y+ y ²
D. y ’=−y
f '(x)= ae-x /(1+ae-x)2 = (1+ae-x -1) / (1+ae-x)2 = 1 /(1+ae-x)-1 /(1+ae-x)2= f(x) -f(x)2=f(x) (1-f'x).

Question 5 : (2 points)
Quelle est la valeur de a pour que f (0) vaille la moitié de la valeur de la limite de f en +oo ?
A. a=0
B. a=1 vrai.
C. a=12
D. a=−1
En plus l'infini, e-x tend vers zéro et f(x) tend vers 1.
f(0) = 1 / (1+a) = ½ ; 1+a = 2 ; a = 1.

Question 6 : (2 points)
Parmi les expressions suivantes, laquelle désigne une autre expression de f (x) ?
A. ex / (1+aex) ; B. e-x / (a+e-x) ; C. ex / (a+ex) vrai ; D. B. e-x / (1+ae-x).
f(x)=1 / (1+ae-x) =ex / [ex(1+ae-x)]=ex / [ex+a].

Question 7 : (2 points)
Une expression d’une primitive de f est donnée par
A. x+a
B. ln(1+ae-x)
On dérive : -ae-x / (1+ae-x)=
C. ln(e−x+a)
 On dérive : -e-x / (e−x+a) = -1/ (1+aex)
D. ln(ex+a). Vrai.
On dérive : ex / (ex+a) = 1 / (1+ae-x).

Dans toutes les questions 8 à 12, on suppose a>0.

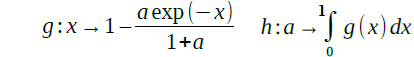
On note g ’ , la fonction dérivée de la fonction g . Une expression de g ’(x ) est
A. a e-x /(1+a) vrai
B.−a e−x / (1+a)
(1+a)
C.1−a e−x / (1+a)
D.(x−a e−x )/ (1+a)

Question 9 : (2 points)
La fonction g est solution de l’équation différentielle
A. y ’= y
B. y ’=−y
C. y ’= y+1
D. y ’=−y+1 vrai
g' = a e-x /(1+a) ; -g = -1+ae-x/(1+a) ; -g+1=ae-x/(1+a)= g'.

...
....

 Question 10 : (2 points)
On définit la suite (vn)n entier naturel par vn=g (n)
A. La suite (vn) n’est pas géométrique vrai
B. La suite (vn) est géométrique de raison 1/e
C. La suite (vn) est géométrique de raison -a/(1+a)
D. La suite(vn) est géométrique de raison -1.
vn =1-ae-n / (1+a).
vn+1 =1-ae-(n+1) / (1+a)=1-ae-n e-1 / (1+a)=1-ae-n  / [e(1+a)]= 1-vn / e.

Question 11 : (2 points)
On peut exprimer h(a) sous la forme
A. (2a+1 – a e−1) / (a+1).
B. (1+ae) /(1+a)
C. (1+ae−1) / (1+a) vrai
D. (1 – ae−1) / (1+a).



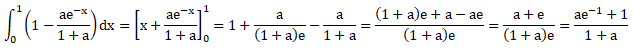
Question 12 : (2 points)
La limite de la fonction h lorsque a tend vers +∞
A. vaut 0
B. vaut 1
C. vaut 1/e vrai
D. n’existe pas.
(a+e) / (e+ae) =(1+e /a) / (e / a +e) tend vers 1/ e si a tend vers plus l'infini.

Question 13 : (2 points)
Soit u une suite géométrique telle que u4=8 et u6=4 alors
A. u10=−4
B. u10=1 vrai
C. u10=2
D. u10=18.
u5 = qu4 ; u6 = q2u4 ; 4 = 8q2 ; q=1/2½ = 2-½.
u7 = q3u4 ; u8 = q4u4 ; u9 = q5u4 ; u10 = q6u4 =8 x1 /8=1.

Question 14 : (2 points)
On pose S=1 – 2+4 – 8+...+1024−2048 . On a
A. S=−1365 vrai
B. S=−1029
C. S=−12 282
D. S=−4095.
S = 1 +4 +16 +...+1024 -(2+8+...+2048).
1 +4 +16 +64 +256 +1024  : somme des 6 premiers  termes d'une suite géométrique de raison 4 et de premier terme 1.
1 +4 +16 +64 +256 +1024=1365.
2+8+32+128+512+2048 : somme des 6 premiers  termes d'une suite géométrique de raison 4 et de premier terme 2.
2+8+32+128+512+2048=2730
S =1365-2730=-1365.

Question 15 : (2 points)
La suite (cn) n entier naturel définie par cn=5n – 7n.
A. a pour limite +∞
B. a pour limite 0
C. a pour limite −∞ vrai
D. n’a pas de limite.
7n((5 / 7)n-1) ; (5 / 7)n tend vers zéro si n tend vers plus l'infini.
Cn tend vers -7n .

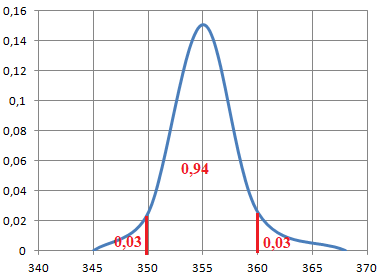
On considère la situation suivante : on étudie la production d’une usine qui fabrique des médicaments, conditionnés en sachets. On choisit un sachet au hasard dans la production journalière. La masse de ce sachet, exprimée en grammes, est modélisée par une variable aléatoire X qui suit une loi normale d’espérance μ=355 . De plus, une observation statistique a montré que 3 % des sachets ont une masse inférieure ou égale à 350 g , ce qui se traduit dans le modèle considéré par : P(X<350)=0,03 .
Question 16 : (2 points)
Quelle est la probabilité, arrondie au centième, de l’évènement « la masse du sachet est comprise entre 350 et 360 grammes » ?
A. 0,06
B. 0,94 vrai
C. 0,97
D. On ne peut pas répondre car il manque des données.


Question 17 : (2 points)
La durée de vie de fonctionnement, exprimée en jours, d’une machine servant à la fabrication des médicaments, est modélisée par une variable aléatoire Y qui suit la loi exponentielle dont l’espérance est égale à 800 jours. Quelle est la probabilité, arrondie au centième, que la durée de
fonctionnement de la machine soit inférieure ou égale à 500 jours ?
A. 0,46 vrai
B. 0,54
C. 1
D. On ne peut pas répondre car il manque des données.
l = 1/800  ; P(Y < 500) =1-exp(-500 / 800) ~0,46.

Question 18 : (2 points)
L’entreprise a déterminé que 2/3 des pharmacies sont satisfaites de ses médicaments, au niveau de confiance de 95 %, avec un intervalle d’amplitude inférieure à 0,05. Quel est le nombre minimal de pharmacies qu’elle a dû interroger pour obtenir ce résultat ?
A. 37
B. 1366 vrai
C. 342
D. 19
amplitude de l'intervalle de confiance = 2 / n½ =0, 05  soit 1 / n½  = 0,025 ; n ~1600.

  
menu