Mathématiques.
Concours contrôleur des douanes 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1.
On considère la fonction f définie sur ]0 ; +∞[ par f (x) = ex −ln(x).
1. Étudier les variations de la fonction g définie sur R par g(x) = xex −1.
Dérivée de x ex en posant u = x et v = ex ; u'=1 ; v' = ex.
g'(x)=u'v+v'u = ex+xex=ex(x+1) >0 sur ]-1; +∞[. g(x) est strictement croissante sur cet intervalle.
g'(x) < 0 sur ]-oo ; -1( , g'x) est strictement décroissante sur cet intervalle.
g'(x) =0 si x = -1 ; g(x) adment un minimum en x = -1.
g(-1) = -e-1 ~-1,467.
Limite en moins l'infini : ex tend vers zéro et g(x) tend vers -1.
Limite en plus l'infini : ex tend vers +oo et g(x) tend vers +oo.
2. En déduire qu’il existe un réel unique a tel que aea =1.
Sur l'intervalle ]-1 ; +oo[, g(x) est continue car dérivable et croît strictement de -1,467 à +oo.
D'après le théorème des valeurs intermédiaires, il existe a appartenant à ]-1 ; +oo[ unique tel que g(a) = 1.
On admet que 0,567 < a < 0,568.
3. Étudier le signe de g(x) sur ]0 ; +∞[.
g(a) = 0 ; g(x) < 0 sur ]0 ; a ] et g(x) > 0 sur ]a ; +oo[.
4. Calculer la fonction dérivée f ′ de f et étudier son signe sur ]0 ;
+∞[.
f '(x) = ex-1/x =( xex-1) / x = g(x) / x.
x est positif sur ]0 ;
+∞[. Le signe de f '(x) est celui de g(x).
g(x) < 0 sur ]0 ; a ] et g(x) > 0 sur ]a ; +oo[.
5. En déduire les variations de f ]0 ; +∞[.
Sur ]0 ; a ], f(x) est décroissante ; sur ]a ; +oo[ f(x) est croissante.
f(x) admet un minimum en x = a.
6. Montrer que f admet un minimumm égal à a+a-1.
f(a) = ea-ln(a).
Or g(a) = 0 ;aea =1 ; f(a) = 1/ a-ln(1/ea) = 1/ a+ln(ea)= a+a-1.
Exercice 2
Partie A
Soit a et b deux réels tels que a < b et f et g deux fonctions continues sur l’intervalle [a ; b].
Montrer que : si pour tout t appartenant à [a ; b], f(t) < g(t) alors 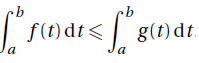
f(t) < g(t) est équivalent à g(t) -f(t) > 0.
D'après la positivité de l'intégrale :
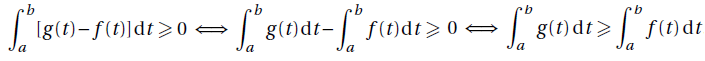
Partie B
Soit n un entier naturel non nul. On appelle fn la fonction définie sur [0 ; +∞[ par fn(x) = ln(1+xn) et on pose
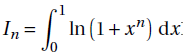
On note Cn la courbe représentative de fn dans un repère orthonormal.
1. a. Déterminer la limite de f1 en +oo.
f1x) = ln(1+x)
En +oo, ln(1+x) tend vers +oo.
b. Étudier les variations de f1 sur [0 ; +∞[.
f '1(x) = 1 / (1+x) >0 sur [0 ; +oo[.
f1(x) est strictement croissante de ln(1)=0 à +oo.
c. À l’aide d’une intégration par parties, calculer I1 et interpréter graphiquement le résultat.
Pour le calcul de I1 on pourra utiliser le résultat suivant :
pour tout x ∈ [0 ; 1], x /(x+1) = 1-1/(x+1).
On pose u = ln(1+x) ; dv =dx ; u' = 1/(1+x) ; v = x.
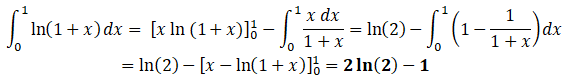
2. a. Montrer que pour tout entier naturel non nul n , on a :0 < In < ln(2).
0 < x < 1 ; 0 < xn < 1 ; 1 < 1+xn < 2 ; ln(1) < ln(1+xn )< ln (2) ;
Intégrer ces trois fonctions entre 0 et 1.
0 < In < ln(2).
b. Étudier les variations de la suite (In).
Pour x < x < 1, la suite xn est décroissante, donc xn+1 < xn.
1+xn+1 <1+xn entraîne ln(1+xn+1 ) <ln(1+xn ) entaîne In+1 < In : la suite (In) est décroissante.
c. En déduire que la suite (In) est convergente.
Les intégrales In sont positives car intégrales de fonctions positives. Elles sont minorées par zéro.
La suite (In) est décroissante et minorée par zéro, donc elle converge.
3. Soit g la fonction définie sur [0 ; +∞[ par : g(x) = ln(1+x)−x.
a. Étudier le sens de variation de g sur [0 ; +∞[.
g '(x) = 1 / (1+x) -1 = -x /(1+x).
g'(x) < 0 sur [0 ; +∞[ ; g(x) est strictement décroissante.
b. En déduire le signe de g sur [0 ; +∞[.
g(0) = 0 ; g(x) = x [ln(1+x) / x-1].
En +oo, ln(1+x) / x tend vers zéro ; g(x) tend vers -oo.
g(x) est négative ou nulle sur [0 ; +∞[ soit ln(1+x)< x.
Montrer alors que pour tout entier naturel n non nul, et pour tout x réel positif, on a : ln(1+xn) < xn.
Quel que soit x > 0, il existe X > 0 tel que x = Xn et donc ln(1+Xn) < Xn.
c. En déduire la limite de (In).
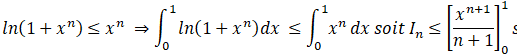
Quand n tend vers plus l'infini 1/(n+1) tend vers zéro : or In > 0, d'après le théorème des gendarmes la limite quand n tend vers +oo de In est zéro.
|
...
|
....
|
Exercice 3.
On considère la suite (un) définie par : u0 = 1 et pour tout n entier naturel, un+1 =1/3 un +n-2.
1. Calculer u1,u2 et u3.
u1=1 / 3 +0-2 = -5 / 3.
u2= -5 / 9 +1-2 = -14 / 9.
u3= -14 / 27 +2-2 = -14 / 27.
2. a. Démontrer que pour tout entier naturel n >4, un >0.
Par récurrence :
Initialisation : u4= -14 / 81 +3-2 = 67 / 81.
u5= 67 / 243 +4-2 = 553 / 243. La relation est vraie au rang 4.
Hérédité : la relation est supposée vraie au rang 4.
1/3 un >0 et +n-2 > 0 ; donc un+1 > 0.
Conclusion: la propriété est vraie au rang 4 et héréditaire, elle est donc vraie pour tout entier n.
b. En déduire que pour tout entier naturel n >5, un >n −3.
Pour n > 5 : un =1/3 un-1 +(n-1)-2 ;
n-1 > 4 et un-1 > 0.
donc un =1/3 un-1 +(n-1)-2 > (n-1) -2 soit un > n-3.
c. En déduire la limite de la suite (un).
La limite en plus l'infini de n-3 est plus l'infini. La limite de la suite (un) est plus l'infini.
3. On définit la suite (vn) par vn = -2un +3n-10,5.
a. Démontrer que la suite (vn) est une suite géométrique dont on donnera la raison et le premier terme.
vn+1 = -2un+1 +3(n+1)-10,5.
vn+1 = -2/3 un -2n+4+ 3(n+1)-10,5 =-2/3 un +n-3,5= 1/3 ( -2 un+3n-10,5)= 1 / 3 vn.
Raison q = 1 /3 ; v0 = -2-10,5 = -12,5.
b. En déduire que : un =25 /4 x(1/3)n+1,5 n-5,25.
vn = -12,5 * (1/3)n = -2un +3n-10,5.
un = 6,25 * (1/3)n +1,5 n -5,25.
c. Soit la somme Sn définie ci-dessous pour tout entier naturel n.
Déterminer l’expression de Sn en fonction de n.
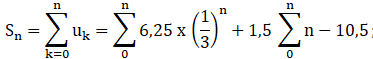
Le 1er terme est la somme des termes d'une suite géométrique de premier terme 6,25 et de raison 1/3 :
6,25 [1-(1/3)n+1] /(1-1/3) =9,375 [1-(1/3)n+1].
Le second terme est la somme des termes d'une suite arithmétique de raison 1 et de premier terme 0.
(0+n) x (n+1) / 2 ; 1,5 n(n+1) / 2 = 0,75 n(n+1).
Sn = 9,375 [1-(1/3)n+1] +0,75 n(n+1) -10,5.
Exercice 4.
Pour rejoindre le sommet S d’une montagne des Alpes à partir d’un point
de départ D, les randonneurs ont la possibilité d’emprunter plusieurs
parcours. La course n’étant pas faisable en une journée, ils doivent
passer une nuit dans l’un des deux refuges se trouvant à la même
altitude de 1 400 mètres sur les parcours existants; les deux refuges
ne sont pas situés au même endroit. On les appelle R1 et R2.
Le lendemain matin, pour atteindre le sommet qui se trouve à 2 500
mètres d’altitude, ils ont deux possibilités : ils peuvent atteindre le
sommet en faisant une halte au refuge R3, ou atteindre le sommet directement.
La probabilité que les randonneurs choisissent de passer par R1 est égale à 1 / 3..
La probabilité de monter directement au sommet en partant de R1 est égale à 3 / 4.
La probabilité de monter directement au sommet en partant de R2 est égale à 2 /3.
1. Tracer un arbre pondéré représentant tous les trajets possibles du départ D jusqu’au sommet S.
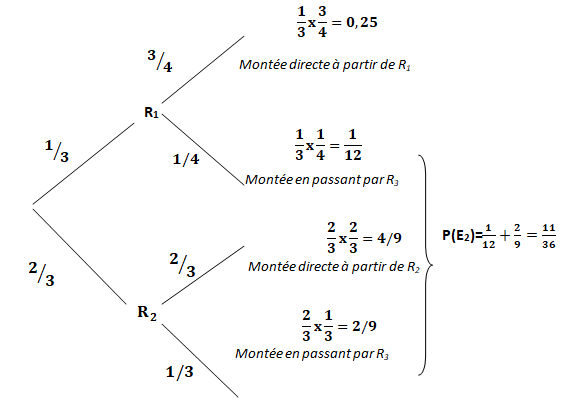
2. Déterminer la probabilité de chacun des évènements suivants :
E1 : « Les randonneurs ont fait une halte au refuge R3 sachant qu’ils ont passé la nuit au refuge R1 »;
P(E1) = P(R1 n R3) / P(R1) =(11 / 36 ) / (1 /3) = 1 /4
E2 « Les randonneurs ont fait une halte au refuge R3 »;
E3 « Les randonneurs ont passé la nuit au refuge R1 sachant qu’ils ont fait une halte au refuge R3 »;
P(E3) = P(R1 n R3) / P(R3) =(1 / 12 ) / (11 /36) = 3 / 11.
E4 « Les randonneurs ont passé la nuit au refuge R2 sachant que, le deuxième jour, ils sont montés directement au sommet S ».
P(direct) = 1 / 4 + 4 / 9 = 25 / 36.
P(E4) = P(R2 n direct) / P(direct) =(4 / 9 ) / (25 /36) = 16 / 25.
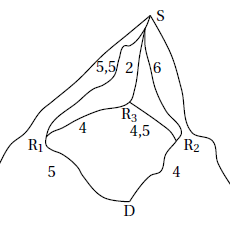
3. On note d(M, N) la distance, en km, à parcourir pour se rendre du point M au point N.
On donne d(D, R1) = 5 ; d(D, R2) = 4 ; d(R1, R3) = 4 ; d(R2, R3) = 4,5 ; d(R3, S) = 2 ; d(R1, S) = 5,5 ; d(R2, S) = 6.
Soit X la variable aléatoire qui représente la distance parcourue par les randonneurs pour aller du départ D au sommet S.
a. Déterminer la loi de probabilité de X.
DR1 S : 10,5 km ; DR2 R3 S : 10,5 km ;
DR2 S : 10 km ; DR1 R3 S : 11 km.
P(X=10)=4 / 9.
P(X=11) = 1 /12.
P(X = 10,5) = 1 / 4 + 2 / 9=17 /36.
b. Calculer l’espérance mathématique de X.
E(X) = 10 x4 /9 + 11 /12 +10,5 x17 /36 ~10,32.
|
|