|
d'après bac La Réunion 2004 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
générateur d'impulsion : le générateur cardiaque : la chirurgie permet d'implanter un stimulateur cardiaque de petite taille : 5 cm de large et 6 mm d'épaisseur. sa masse est d'environ 30 g.
Stockage d'énergie : le flash électronique. L'énergie libérée en un temps très bref par l'éclair d'un flash est au préalable stockée dans un condensateur, de grande capacité, chargé par quatre piles identiques en série équivalente à un générateur de fem U=6 V. Elles contiennent une énergie totale E= 18 kJ lorsqu"elles sont neuves. Pour un fonctionnement optimal la moitié de cette énergie est transférable au condensateur. Au dela elles doivent être changées. L'autonomie est de l'ordre de 100 à 3500 éclairs et le temps de recharge après un éclair est de l'ordre de 0,2 à 11 s. La durée de l'éclair peut être limitée par un circuit électronique, ce qui explique les fourchettes données. Les indications en gras correspondent à des éclairs d'intensité lumineuse et de durée maximales résultant de la décharge complète du condensateur.
Oscillations électriques : le détecteur de fraude.
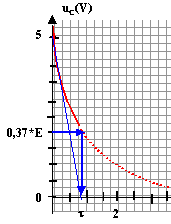
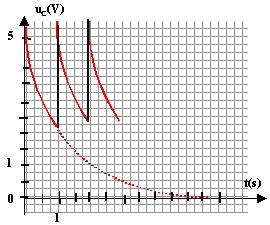
corrigé Le condensateur est pratiquement chargé au bout d'une durée égale à 5t. (t constante de temps du dipôle RC) La valeur de la résistance étant très faible, t est proche de 0 s. Le condensateur se charge presque instantanément.
sue la courbe uC=f(t) les droites noires correspondent à la charge du condensateur (la tension uC est croissante lors de la charge du condensateur. ( droite car charge très rapide) Lorsque le condensateur est complètement chargé, il n'y a pas de courant qui circule et l'intensité i = 0 A. lecture sur la
courbe uC=f(t) à t=0 : uC maxi voisin de 5,5 V = E
La tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles : dans ce cas les flèches qui symbolyse i et uR ont le même sens , donc uR= -Ri q=CuC ; i=dq/dt = CduC/dt or uR= -Ri soit uR= -RCduC/dt ; duC/dt + 1/(RC) uR=0 lors de la décharge d'après la loi d'additivité des tensions: uC = uR par suite : duC/dt + 1/(RC) uC=0 et par identification t=RC. résistance = tension (V) / intensité (A) = [U][I]-1 capacité (F) = charge (coulomb) / tension (volt) = intensité (A) * temps(s) / tension (V) = [I][T][U]-1. RC : [U][I]-1 [I][T][U]-1soit homogène à une durée. Détermination graphique de t. à t = t, la tension aux bornes du condensateur est égale à 37% de sa valeur maximale (uC = 0,37*E =0,37*5,5 = = 2 V). On trouve t proche 0,8 s
ou bien on trace la tangente à la courbe uC(t) à t =0 s. La tangente coupe l'asymptote horizontale uC = 0 à l'instant t =t. RC= 0,8 avec C=
470 10-9 F soit R = 0,8 / 470 10-9 = 1,7 106 ohms.
alors E = uC e = 2 e = 2*2,71 = 5,42 V valeur de E est en accord avec celle trouvée ci-dessus uC(t1) = E exp(-t1/t) = 2 exp(-t1/t) =2/E = 2/5,5 =0,364 ; -t1/t =ln 0,364 = -1,01 donc t1 = t La durée Dt séparant deux impulsions consécutives doit être proche t (t durée nécessaire pour que uC atteigne ulimite ). Nombre de battements du cœur par minute : un battement toutes les 0,8 s soit 60/0,8 = 75 battements par minute.
La moitié de l'énergie totale des piles est utilisée soit 9000 J pour 1 éclair E =9000/100 = 90 J E = ½CU² soit une capacité C =2E / U² = 2*90/ 6² = 5 F capacité très grande par rapport aux valeurs habituelles(de l'ordre de 10-6 ou 10-9 F). La recharge dure 11 s donc 5t = 11 soit t = 2,2 s. t = RC d'où R=t/C = 2,2/5 =0,44 W
T0= 2p(LC)½ soit T02= 4p2LC avec T0 = 1/f = 1/ 107= 10-7s. C= T02/(4p2L) =10-14/(4*3,14²*5 10-7)=5 10-10 F = 0,5 nF.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
électrolyse Cet exercice est un QROC (questions à réponses ouvertes et courtes). A chaque affirmation, vous répondrez par VRAI ou FAUX. Toute réponse doit être accompagnée de justifications ou de commentaires brefs (définitions, calculs, exemples ou contre- exemples...).
corrigé a- vraie La transformation chimique n'est pas spontanée : le générateur, en apportant de l'énergie électrique, permet à la transformation forcée de se produire b- vraie Cu2+(aq) + 2 e- = Cu (s) il se forme un dépôt de cuivre solide sur le flanc
L'ajout d'eau dilue la solution et fait chuter la concentration en ion cuivre II |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
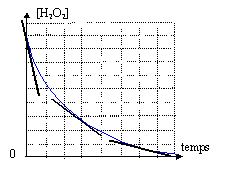
catalyse homogène L'eau oxygénée est un antiseptique. Les molécules H2O2 sont capables d'oxyder les ios tartrates C4H4O62- suivant : Cette transformation sera considérer comme totale. On mélange un volume V1 d'eau oxygénée à la concentration c1 et un volume V2 de solution contenant des ions tartrates à la concentration c2. La température est 20°C et le mélange réactionnele est acidifié. La transformation chimique s'effectue à volume constant. La durée de cette transformation est de l'ordre de plusieurs semaines. Etude cinétique : un élève a obtenu le tableau d'évolution du système suivant avec n1<5n2 :
Catalyse homogène : pour réaliser la transformation précédente de façon instantanée, on peut la catalyser par les ions cobalt II Co2+ qui donnent une couleur rose aux solutions. Ce catalyseur permet aux réactifs de parvenir aux produits par un chemin énergétiquement moins exigeant. Ce chemin peut être modéliser par : 10Co3+ + C4H4O62- +10 H2O = 8H3O+ + 4CO2(g) + 10Co2+(R2) Le mélange réactionnel comporte 60 mL d'une solution contenant des ions tartrate à 0,2 mol/L, 10 mL d'eau oxygénée à 11 mol/L et 5 mL d'une solution de sel de cobalt II à 0,15 mol/L L'évolution temporelle de la concentration en ion cobalt III présents dans le mélange réactionnel est représentée ci-dessous : 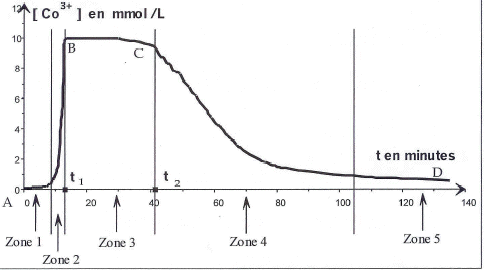
Les ions Co3+ donnent une couleur verte aux solutions.
corrigé
C4H4O62- est le réactif limitant alors n2 - xmax = 0 soit xmax = n2 or n1 < 5n2 , donc le réactif limitant est H2O2 Les ions H3O+ sont l'un des réactifs, d'après l'équation : ces derniers sont apportés par l'ajout d'acide La courbe donnant l'évolution de la concentration en eau oxygénée en fonction du temps est décroissante, car le réactif H2O2 est consommé. La concentration étant un facteur cinétique.
v = 1/V dx/dt où V est le volume réactionnel constant au cours de la transformation. D'après le tableau d'avancement la quantité de matière H2O2 est n H2O2 = n1 - 5x =[H2O2] V d'où x =( n1 -[H2O2] V) / 5 dx/dt = -V/5 d[H2O2] / dt soit v = -1/5 d[H2O2] / dt Comment évolue la vitesse au cours du temps ? La vitesse volumique de réaction diminue au cours du temps : cette vitesse est obtenue graphiquement à partir du coefficient directeur de la tangente à la courbe ci-dessus. La tangente est très inclinée par rapport à l'horizontale à t=0, puis la tangente se rapproche peu à peu de l'horizontale. La concentration
en H2O2 diminue au cours du temps : la probabilité de
rencontre efficace entre les réactifs est de plus en plus faible au
cours du temps.
Les ions cobalt III donnant une coloration verte aux solutions, on peut suivre par spectrophotométrie l'évolution de leur concentration. L'absorbance A de la solution, pour une longueur d'onde donnée, est proportionnelle à la concentration des l'espèces colorantes (loi de Beer-Lambert). Suivre l'évolution de l'absorbance, c'est donc suivreà l'évolution de [Co3+] au cours du temps. Zone 1: les ions cobalt II colorent la solution en rose. Zone 3: la concentration en ions cobalt III est maximale, la solution est bien verte. Zone 5: [Co3+] faible, les ions Co3+ se sont transformés en ions Co2+ et la solution reprend la couleur rose. Zone 2 : couleur verdâtre du fait de la présence de Co3+ et de Co2+: la réaction (R1) se produit. Zone 3: [Co3+] maximale, mais elle commence à diminuer. La réaction (R2) débute. Zone 4: [Co3+] diminue, les ions Co3+ sont consommés, donc réaction (R2). Vitesse de réaction Tracer la tangente en t3 à la courbe [Co3+]= f(t). Puis déterminer son coefficient directeur qui vaut d[Co3+]/dt . Repport de sa valeur dans l'expression donnant la vitesse. Rôle du catalyseur Le catalyseur n'apparaît pas dans l'équation chimique, car il est totalement régénéré à l'état final. La courbe 1 montre que [Co3+] initiale est nulle alors [Co2+] est maximale. de plus [Co3+] se rapproche de zéro dans l'état final,en conséquence [Co2+] est maximale et égale à [Co2+] initiale. le tableau d'avancement indique nCO2 fin = finale = 4xmax. Le catalyseur ne change pas l'avancement final xmax, donc nCO2 fin reste identique avec ou sans catalyseur catalyse homogène : le catalyseur et les réactifs sont dans une même phase liquide.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|