|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||
|
|||
|
|
En levant les yeux vers le ciel étoilé, on aperçoit une multitude de points brillants qui donnent l'impression d'une immense profusion. Identifier un astre dans un tel ensemble apparaît comme une gageure. Une observation à l'œil nu permet de repérer un petit nombre d'étoiles brillantes et quelques constellations. Avec une pupille dont le diamètre maximal dans l'obscurité est voisin de 6 mm, l'œil humain ne peut capter qu'une quantité de lumière assez limitée. Les étoiles de plus faible éclat sont perceptibles seulement grâce à des instruments optiques. On distingue 2 types principaux d'instruments : la lunette astronomique et le télescope. Tous deux comportent essentiellement 2 parties : un collecteur de lumière (ou objectif) qui collecte et focalise les rayons lumineux en un point appelé foyer, en donnant une image intermédiaire que l'on peut observer grâce à un oculaire qui joue le rôle d'une loupe. La lunette astronomique et le télescope se différencient par la nature du collecteur de lumière : - pour la lunette, c'est un ensemble de lentilles assimilable à une lentille convergente. - pour le télescope, c'est un miroir sphérique concave. La photographie ci-dessous est celle d'un télescope d'amateur qui comprend le " chercheur " et le télescope (type Newton) proprement dit. 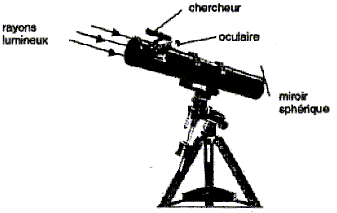 Le " chercheur " est une petite lunette astronomique de faible grossissement destinée à faciliter le pointage de la zone du ciel que l'on souhaite observer. Dans tout ce qui suit, on ne s'intéresse qu'au télescope proprement dit. I- Etude préliminaire : propriétés des miroirs
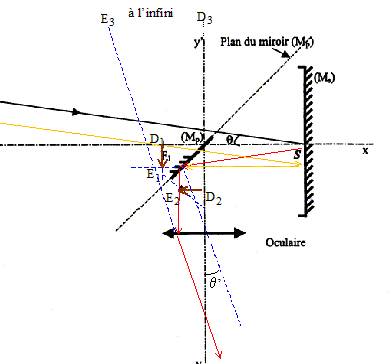
II- Observation de la Lune à l'aide du télescope d'amateur (télescope de Newton) 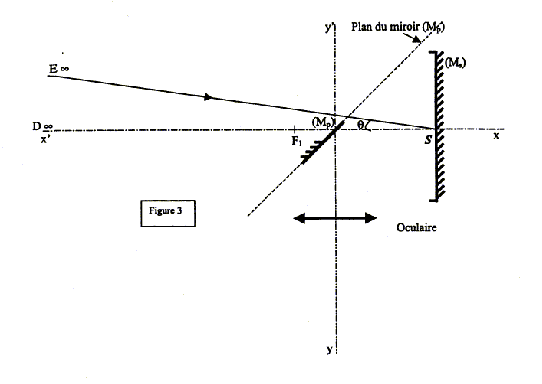 Le télescope est formé principalement : - du miroir sphérique ou objectif (MS) de distance focale F1S = f1. - d'un petit miroir plan (MP) incliné à 45° par rapport à l'axe optique du miroir principal et placé entre celui-ci et son foyer (voir figure 3), les surfaces réfléchissantes des deux miroirs étant face à face. - d'un oculaire d'axe yy' perpendiculaire à xx', assimilable à une lentille convergente de distance focale f '2. L'astronome oriente l'axe du télescope vers le centre de la Lune D supposé situé à une distance infinie et veut observer un détail ponctuel E à la surface du sol lunaire. Les rayons issus de E font l'angle q faible avec l'axe optique. Le miroir principal (MS) donne de D et E les images respectives D1 et E1. D1E1 sert d'objet pour le miroir plan (MP) qui en donne une image D2E2. D2E2 sert d'objet pour l'oculaire qui en donne l'image définitive D3E3.
III- Grossissement On donne les caractéristiques du télescope : Diamètre du collecteur 114 mm ; Distance focale du miroir sphérique F1S = f1 = 910 mm ; Distance focale de l'oculaire : f '2 = 9 mm. D'autre part q = 0,5° voisin de 8,7´10-3 rad, valeur qui permet de confondre q et tanq.
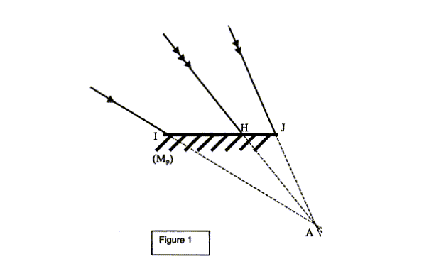
rayons réfléchis correspondant aux rayons incidents extrêmes passant par I et J ainsi qu'au rayon intermédiaire passant par H. Construire A' symétrique de A par rapport au plan du miroir ; l'angle d'incidence étant égal à l'angle de réflexion, tous les rayons réfléchis à construire passe par A'.
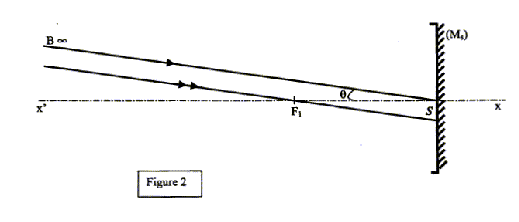
après réflexion sur le miroir les rayons issus de B et passant respectivement par F1 et S.
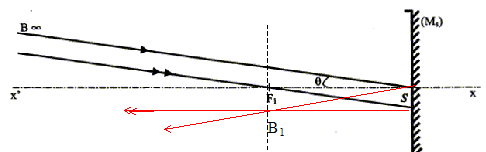
B1 'image de B. Tout rayon incident passant par F1 se réfléchit parallèlement à l'axe x'x du miroir. B étant à l'infini son image B1 se trouve dans le plan focal du miroir. Le rayon incident passant par S, se réfléchit en passant par B1. rayons lumineux permettant d'obtenir l'image D1E1.
E étant à l'infini son image E1 se trouve dans le plan focal du miroir convergent. position de D2E2 : symétrique de D1E1 par rapport au plan du miroir ; les dimensions de D1E1 et D2E2 sont identiques du fait de la symétrie. Le miroir étant incliné à 45 °et D1E1 étant verticale, D2E2 est horizontale. D2E2 est dans le plan focal objet de l'oculaire. L'image définitive D3E3 se trouvee à l'infini Avec ce réglage l'oeil observe sans fatigue, sans accomoder. D1E1 en fonction de q et f1 : triangle SD1E1: tan q = D1E1/ SF1 ; tan q voisin q d'où q = D1E1/ SF1 = D1E1/ f1 . D1E1 = q f1 = 8,7 10-3 * 0,91 = 7,9 10-3 m. q ' en fonction de D2E2 et f '2 : D1E1 = D2E2 et tan q' = D2E2/ f '2 ; tan q' voisin q' d'où q' = D2E2/ f '2 . q' =7,9 10-3 / 9 10-3 = 8,8 10-1 rad. grossissement du télescope comme le rapport G = q '/ q = [D2E2/ f '2 ] / [D1E1/ f1 ]avec D1E1 = D2E2 d'où G= f1 / f '2 = 910/9 = 100. Avec quel oculaire le grossissement sera-t-il maximal ? pour l'oculaire de 20 mm le grossissement vaut : 910 / 20 = 46 Le grossissement est maximal avec l'oculaire de 9 mm.
|
||
|
|