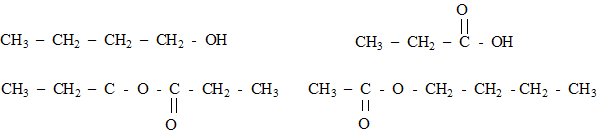|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La chimie au service de la parfumerie Pour sa création au printemps 2006, un illustre parfumeur décide d'utiliser l'odeur de pomme et celle de la banane, effluves de son nouveau parfum. Il choisit d'utiliser l'arôme naturel de pomme mais, pour des raisons économiques, de synthétiser une molécule à odeur de banane. Un parfum de pomme : Une des molécules présentes dans l'arôme naturel de pomme est un ester E de formule semi-développée : 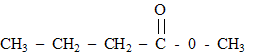
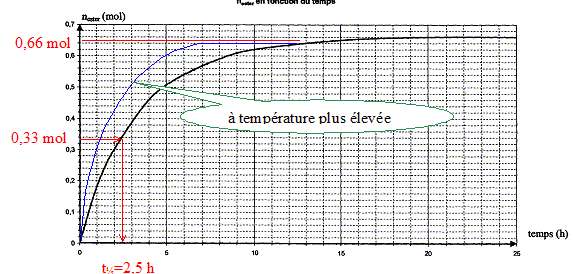
2. Un parfum de banane : L'ester à odeur de banane se nomme éthanoate d'isoamyle ou éthanoate de 3-méthylbutyle, en nomenclature officielle. Sa formule semi-développée est : 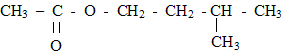 Le parfumeur décide de synthétiser cet ester, son extraction étant trop coûteuse. Il utilise alors un mélange d'acide éthanoïque et d'alcool isoamylique, de formules semi-développées respectives : CH3-COOH (acide éthanoïque) et (CH3)2- CH - CH2 - CH2 - OH (acide isoamylique) Avant de se lancer dans une production à grande échelle, le parfumeur décide de réaliser l'expérience. Pour cela, il introduit dans un erlenmeyer 1,00 mol d'acide éthanoïque et 1,00 mol d'alcool isoamylique. Le mélange est maintenu à température constante. Il prélève régulièrement un échantillon du mélange qu'il refroidit brutalement puis il dose l'acide restant par une solution d'hydroxyde de sodium. La quantité de matière d'acide est notée nA. Les résultats sont rassemblés dans le tableau ci-dessous :
corrigé nom de l'ester : butanoate de méthyle. les formules semi-développées de l'acide carboxylique et de l'alcool acide butanoïque CH3-CH2-CH2-COOH et le méthanol CH3OH l'équation associée à la réaction d'estérification : CH3-CH2-CH2-COOH + CH3OH = CH3-CH2-CH2-COO-CH3 + H2O éthanoate de butyle : CH3-COO-CH2-CH2-CH2-CH3.
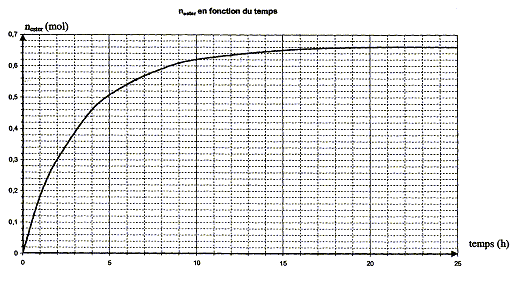
quantité de matière d'ester nester formée aux dates des prélèvements : nA = 1,00-x soit x = 1,00-nA ; nester = x =1,00-nA
au delà de t = 20 heures la composition du milieu réactionnel ne change plus ; un état d'équilibre chimique est atteint xf = nester f = 0,66 mol. taux d'avancement final t de la transformation : t = xf /xmax = 0,66 / 1 = 0,66 ( 66 %). t <1 donc cette
transformation n'est pas totale : elle est limitée
par la réaction inverse, l'hydrolyse de l'ester. en utilisant un excès de l'un des réactifs ( le moins couteux), on déplace l'équilibre dans le sens direct, formation de l'ester. éliminer l'un des produits au fur et à mesure qu'il se forme ( le plus volatil, par distillation si cela est possible) interprétation qualitative de la variation de la vitesse de réaction au cours du temps : à une date donnée t, la vitesse volumique est proportionnelle à [dx/dt]t ; c'est à dire au coefficient directeur de la tangente à la courbe nester = f(t) à la date t. Or au cours du temps, les tangentes à cette courbe sont de plus en plus inclinées sur l'horizontale : la vitesse volumique diminue : cela est du à la diminution des concentrations ( facteur cinétique) des réactifs. temps de demi-réaction t1/2 : durée au bout de laquelle l'avancement x est égal à la moitié de l'avancement final ( dans ce cas xt½=0,33 mol)
but du refroidissement brutal effectué avant chaque dosage : blocage cinétique de l'estérification.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
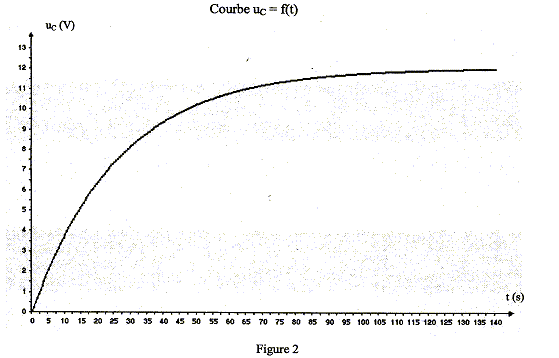
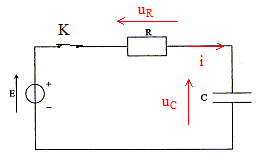
Etude théorique d'un dipole RC soumis à un échelon de tension : Le montage du circuit électrique schématisé ci-contre (figure 1) comporte : - un générateur idéal de tension de force électromotrice E = 12,0 V ; - un conducteur ohmique de résistance R inconnue ;- un condensateur de capacité C = 120 µF ;- un interrupteur K. Le condensateur est initialement déchargé. À la date t = 0, on ferme l'interrupteur K. 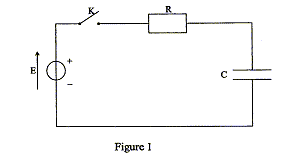 Par ailleurs, on note q la charge de l'armature du condensateur qui se chargera positivement.
Application : Au dipôle RC précédemment étudié, on associe un montage électronique qui commande l'allumage d'une lampe : la lampe s'allume lorsque la tension uc aux bornes du condensateur est inférieure à une valeur limite ual =6,0V; la lampe s'éteint dès que la tension uc aux bornes du condensateur est supérieure à cette valeur limite ua1= 6,0 V. Le circuit obtenu (figure 3) est le suivant : 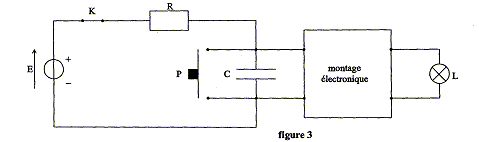 Fonctionnement du bouton poussoir : Lorsqu'on appuie sur le bouton poussoir, ce dernier entre en contact avec les deux bornes du condensateur et se comporte comme un fil conducteur de résistance nulle. Il provoque la décharge instantanée du condensateur. Lorsqu'on relâche le bouton poussoir, ce dernier se comporte alors comme un interrupteur ouvert.
corrigé Etude théorique d'un dipole RC soumis à un échelon de tension :
expression de UR en fonction de i : uR= Ri expression de i en fonction de la charge q du condensateur : i = dq/dt ( q charge de l'armature supérieure du condensateur) relation liant q et uc : q= Cuc. expression de i en fonction de la capacité C et de la tension uc : i = Cduc/dt loi d'additivité des tensions : E= uR + uc. équation différentielle notée (1) à laquelle obéit uc : E= RCduc/dt + uc. uc = E (1- exp(-t/t)) est solution de l'équation différentielle ; dériver par rapport au temps : duc/dt = E/(RC)exp(-t/t) repport dans (1) : E= Eexp(-t/t) + E (1- exp(-t/t)), vérifiée quel que soit le temps, donc uc = E (1- exp(-t/t)), avec t = RC, est solution de l'équation différentielle vérification de la condition initiale : à t = 0 le condensateur n'est pas chargé et uc(0) = 0. uc (0)= E (1- exp(-0/t)) = E(1-1) = 0 la fonction uc = E (1- exp(-t/t)) vérifie bien la condition initiale. analyse dimensionnelle du produit t = RC : R : résistance soit tension / intensité C : capacité soit charge / tension et une charge est une intensité fois un temps d'où C : intensité * temps / tension par suite RC a la dimension d'un temps et t
est bien homogène à une durée.
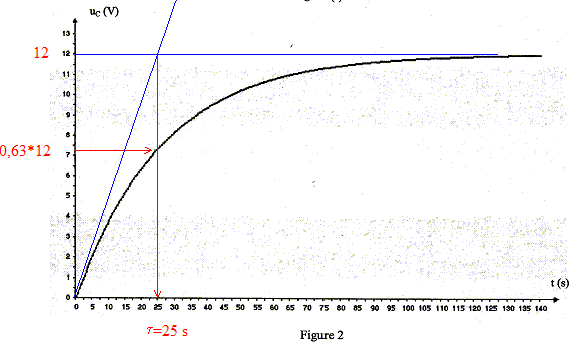
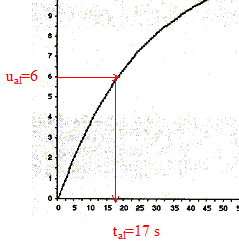
Application : Le condensateur est initialement chargé avec une tension égale à 12 V, la lampe est éteinte. On appuie sur le bouton poussoir P : on provoque la décharge instantanée du condensateur et uc s'annule. Or la lampe s'allume lorsque la tension uc aux bornes du condensateur est inférieure à une valeur limite ual =6,0V : donc la lampe s'allume. Lorsqu'on relâche le bouton poussoir, ce dernier se comporte alors comme un interrupteur ouvert. Le condensateur relié au générateur de tension E, se charge ; la tension uc à ses bornes augmente jusqu'à atteindre la valeur E=12 V. La constante de temps du dipôle RC utilisé est t = 25 s. Le condensateur se charge très lentement ( 5 t = 125 s). La lampe reste allumée tant que la tension aux bornes du condensateur reste inférieure à ua1= 6,0 V, puis la lampe s'éteint. expression littérale de la date tal, à laquelle la tension aux bornes du condensateur atteint la valeur limite ual en fonction de ual, E et t : ual = E (1- exp(-tal/t)) ; ual / E =1- exp(-tal/t) ; 1-ual / E = exp(-tal/t) ln(1-ual / E )= -tal/t ; tal = -t ln(1-ual / E ) tal = -25 ln(1-6/12) = -25 ln 0,5 = 17 s. Détermination graphique de la valeur de
tal à l'aide de la courbe uc =
f(t) : La tension aux bornes du générateur E étant constante, pour augmenter la durée d'allumage tal = -t ln(1-ual / E ), il faut augmenter t : donc augmenter la résistance R ou/et augmenter la capacité C du condensateur.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On s'intéressera dans cet exercice à l'étude de la houle en haute mer, à savoir en eau profonde, et aux caractéristiques de celle-ci en fonction d'une échelle en intensité appelée échelle de Beaufort. Dans une revue maritime traitant du sujet, on peut lire le texte suivant : Lorsque le vent souffle sur une mer calme, le frottement de l'air crée de petites rides puis des vaguelettes et enfin des vagues à mesure que la vitesse du vent augmente. L'ensemble de ces vagues, généré sur un intervalle de temps plus ou moins long, constitue la houle. Cette houle peut être décrite à l'aide de trois paramètres. - La hauteur h, définie comme la distance verticale entre le sommet de la crête et le fond du creux de la vague. - La longueur L, comme la distance entre deux crêtes ou deux creux successifs. - La cambrure, définie comme le rapport de sa hauteur sur sa longueur - La cambrure, définie comme le rapport de sa hauteur sur sa longueur. Ainsi le phénomène de la houle peut être considéré comme une onde mécanique. Aussi on assimilera dans tout l'exercice la houle à une onde progressive périodique sinusoïdale rectiligne dont les paramètres caractéristiques peuvent varier suivant l'état de la mer. 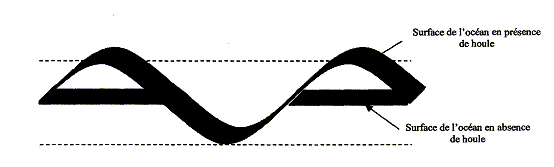
L'échelle de Beaufort établie en 1805 - du nom de l'amiral de la marine britannique Francis Beaufort - graduée de 0 à 12 permet de caractériser la vitesse des vents. L'état de la mer étant directement lié à la vitesse du vent, cette échelle permet également de caractériser l'état de la mer et donc les conditions de navigation. Le tableau ci-dessous présente les derniers degrés d'une échelle de Beaufort simplifiée que le candidat utilisera dans la suite de l'exercice. On se place dans le cas où la cambrure des vagues notée Ca est telle que Ca = 1/7. On gardera cette valeur de cambrure pour tout le reste de l'exercice.
corrigé 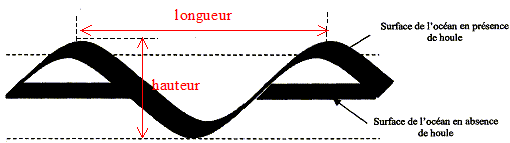
le terme "longueur " du texte d'introduction est associé à la période spatiale, ou longueur d'onde, distance séparant deux crêtes consécutives. définition de la longueur d'onde : plus petite distance séparant deux points du milieu se trouvant dans le même état vibratoire. La période temporelle, inverse de la fréquence, permet de caractériser une onde mécanique. définition de la période temporelle : plus petite durée au bout de laquelle un point du milieu se retrouve dans le même état vibratoire. La cambrure, définie comme le rapport de sa hauteur sur sa longueur : Ca = h/L longueur des vagues pour les degrés 6, 8, 10 et 12 de l'échelle de Beaufort : L= h/Ca = 7 h.
expression reliant la longueur L, la célérité v et la fréquence f de l'onde : L= v/f célérité v de l'onde associée : v = L/T
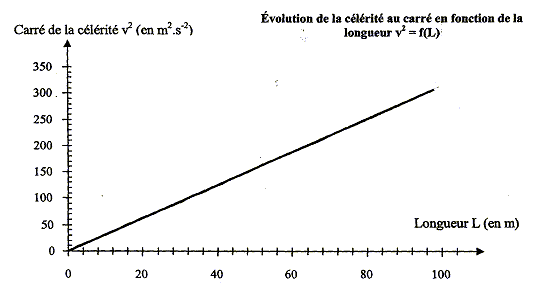
type de courbe : droite passant par l'origine : v² et L sont proportionnelles ; v² = k L avec k une constante égale au coefficient directeur de la droite. k = 310/ 100 = 3,1 m s-2. définition d'un milieu dispersif : dans un milieu dispersif la célérité des ondes dépend de leur fréquence. expression littérale reliant la célérité v de la houle à sa fréquence f : v² = 3,1 L avec L= l ( longueur d'onde) ; de plus l = v/f d'où :
v² = 3,1 v/f soit v= 3,1/f
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||