|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
D'où peut bien provenir l'énergie du Soleil ? C'est seulement en 1920 que le voile est levé, par les Britanniques Francis William ASTON et Arthur EDDINGTON : les noyaux d'atomes d'hydrogène, le principal constituant solaire, se transforment en hélium en fusionnant. Une réaction qui libère une énergie faramineuse. L'objectif du projet ITER est de démontrer la possibilité scientifique et technologique de la production d'énergie parla fusion des atomes. La fusion contrôlée représente un défi scientifique et technologique majeur qui pourrait répondre au problème crucial de disposer, à plus ou moins long terme, de nouvelles ressources énergétiques. A côté de l'énergie de fission, l'énergie de fusion représente l'espoir d'avoir une source d'énergie propre et abondante au cours du XXIe siècle. A l'heure où la raréfaction des énergies fossiles est prévue d'ici 50 ans, il est d'une importance vitale d'explorer le potentiel de toutes les autres sources d'énergie. Etude de la réaction de fusion : Le concept solaire de production d'énergie est basé sur une réaction dont la probabilité de se réaliser est extrêmement faible sur notre planète. Mais l'idée reste bonne ! Il "suffit" de remplacer l'hydrogène par des noyaux qui ont un maximum de chance de fusionner sur Terre, en l'occurrence, ceux de deutérium et de tritium, deux isotopes de l'hydrogène [...] en les chauffant à des températures très élevées, de l'ordre de 100 millions de degrés. " C'est donc sur cette réaction que se concentrent les recherches concernant la fusion contrôlée.
|
||||||||||||||||||||||||
corrigé Etude de la réaction de fusion : 21H + 31H
---> 42He + 10n
Variation de masse au cours de la réaction de fusion d'un noyau de deutérium et d'un noyau de tritium : Dm= m(42He) + m(10n) - m(31H) - m(21H) Dm=4,00150+1,00866-3,01550-2,01355 = -1,889 10-2 u -1,889 10-2 *1,66054 10-27 =-3,13676 10-29 kg. La masse des produits est inférieure à celle des réactifs ; la masse est une forme de l'énergie : le signe négatif traduit la libération d'énergie dans le milieu extérieur. Energie produite par cette réaction de fusion : E= Dm c²= -3,13676 10-29*(2,998 108 )2 = -2,819 10-12 J -2,819 10-12 /1,602 10-13
= - 17,60 MeV. masse (kg) / masse d'un noyau (kg) = 1,0
10-3 / (2,01355*1,66054 10-27) = 3,0 1023
noyaux. 1,5 10-3 / (3,0155*1,66054 10-27) = 3,0 1023 noyaux. Energie, en MeV puis en Joule, que l'on pourrait espérer obtenir si on réalisait la réaction de fusion de 1,0 g de noyaux de deutérium avec 1,5 g de noyaux de tritium dans le réacteur ITER : 17,60 * 3,0 1023 = 5,28 1024 MeV 5,28 1024 *1,602 10-13 = 8,5 1011 J. La tonne d'équivalent pétrole (tep) est une unité d'énergie utilisée dans l'industrie et en économie. Elle sert à comparer les énergies obtenues à partir de sources différentes. 1 tep représente 4,2 1010J, c'est-à-dire l'énergie libérée en moyenne par la combustion d'une tonne de pétrole. Calcul, en tep, de l'énergie libérée par la fusion de 1,0 g de deutérium et de 1,5 g de tritium : 8,5 1011/4,2 1010
= 20 tep. ITER est un progrès et un espoir pour la production d'énergie car à masse de combustible égale il libère 10 fois plus d'énergie. De plus "l'énergie de fusion représente l'espoir d'avoir une source d'énergie propre et abondante" les matières premières sont abondantes et les déchets radioactifs sont moindres.
Quelques précisions sur le tritium : Le deutérium est naturellement présent
sur Terre alors que le tritium lui, est très rare. Il est donc obtenu à
partir du lithium 63Li très abondant dans la
croûte terrestre et les océans. Pour ce faire, un échantillon de
lithium est bombardé par des neutrons, il se forme de l'hélium 42He
et du tritium 31H. 63Li + 10n--->
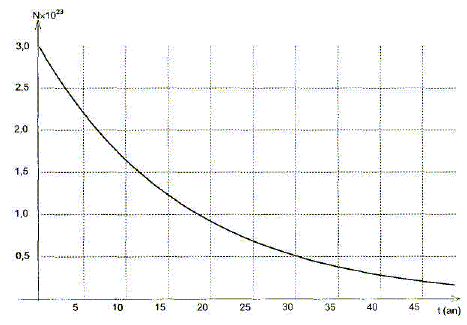
31H + 42He Equation de la désintégration envisagée sachant qu'il se forme un isotope de l'hélium : 31H --->A2He + 0-1e conservation du nombre de nucléons : 3 = A méthode d'Euler : On veut étudier l'évolution au cours du temps du nombre de noyaux présents dans un échantillon de tritium. On sait que le nombre de désintégrations au cours du temps est proportionnel au nombre de noyaux présents : D N(t) / Dt =-lN(t) (1) où l est la constante radioactive du tritium. On prendra l = 5,65 10-2 an-1 = 1,79 10-9 s-1 . La méthode d'Euler est une méthode numérique qui permet de calculer de façon approchée le nombre N de noyaux présents à différentes dates en utilisant la relation suivante : N(t + Dt) = N(t) + D N(t) (2) Expression de N(t + D t) en fonction de N(t), l et Dt. (Dt est le pas de résolution) : (1) donne : D N(t) =-lN(t) Dt puis repport dans (2) d'où N(t +
Dt) = N(t) -lN(t) Dt
N(2) = N(1) -lN(1) Dt = 2,83 1023 -5,65 10-2*2,83 1023*1 = 2,67 1023.
Valeur du temps de demi-vie t1/2 : l t½ = ln2 ; t½ = ln2 / l = ln 2 / 5,65 10-2 = 12,3 ans.
Calcul du nombre de noyaux de tritium qui se désintègrent naturellement en 1000 s : N(t + Dt) = N(t) -lN(t) Dt ; N(1000) = N(0) -lN(0) *1000 N(0) - N(1000 ) = lN(0) *1000 = 1,79 10-6 * 3,0 1023 = 5,4 1017 noyaux. valeur très inférieure à N0 : on peut ignorer la désintégration naturelle du tritium. masse de tritium correspondante : 5,37 1017 * 3,01550=1,62 1018 u = 2,7
10-9 kg.
|
|||||||||||||||||||||||||
|
|