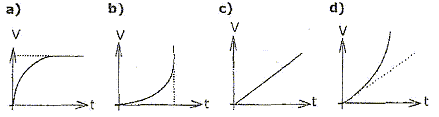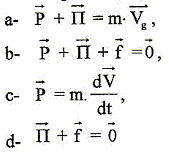|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
|
|
|
||
|
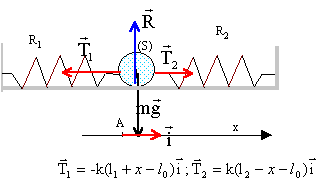
Aide aux calculs : 6,24 = 2p ; p² = 10 = 3,2² ; 1,9 = 0,11 ; 438*14,7=6440 ; 438/14,7=29,8 ; 14,7/438 = 3,36 10-2. A- Modélisation de l'ensemble {dôme, ressort} Un mobile autoporteur de masse m, de centre d'inertie G ( modélisant le dôme) est relié aux extrémités A et A' de deux ressorts identiques ( raideur k, longueur à vide l0). Les ressorts modèlisent le "spider, qui permet de maintenir le dôme au centre. Les extrémités B et B' de ces ressorts sont fixes. L'étude est faîte dans le référentiel terrestre galiléen. Les ressorts travaillent toujours en extension et sont à spires non jointives.  Le système initialement au repos, est écarté de sa
position d'équiliobre en déplaçant G le long de l'axe des ressorts. O
correspond à la position de G à l'équilibre. Les frottements sont
négligeables dans cette première partie.
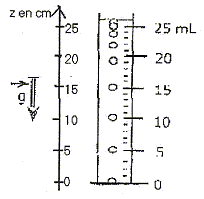
Etude expérimentale : On pèse le mobile : m= 62,4 g, puis on réalise l'expérience sur une table à numériser. Cette table permet l'enregistrement des positions succssives de G et de connaître les valeurs de l'élongation x(t), dans un repère lié à la table. Un logiciel de traitement des données permet d'afficher diverse représentations graphiques et de réaliser leur modélisation.
Etude énergétique :
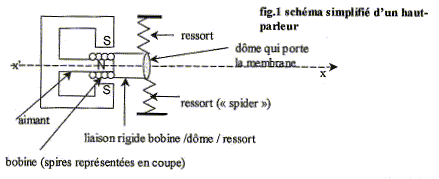
Un dispositif placé sur le mobile permet d'introduire des frottements : En utilisant deux valeurs consécutives de l'amplitude, donner un ordre de grandeur du pourcentage de l'énergie perdue par l'oscillateur en une période. 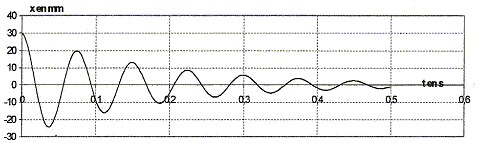 B- Modélisation du haut parleur : Etude de la force magnétique : la bobine, dont les spires sont représentées en coupe peut se déplacer sur le noyau central de l'aimant : parcourue par un courant électrique, elle est soumise à une force magnétique Fm de direction parallèle à l'axe x'x. Cette bobine est, en outre accrochée en A à un ressort à spires non jointives de coefficient de raideur k= 438 N/m, dont l'autre extrémité B est fixe. Lorsque la bobine est parcourue par un courant I, le ressort s'allonge et une règle graduée permet de mesurer l'allongement x du ressort Un logiciel d'aquisition donne les résultats suivants : 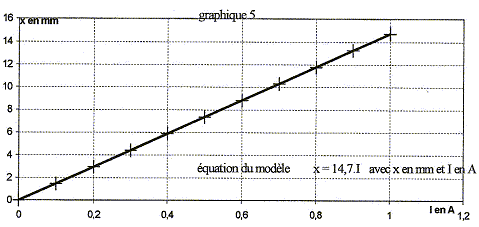
Le haut parleur en fonctionnement : on utilise l'ensemble aimant-bobine pour construire un haut-parleur. On utilisera les notations suivantes : x: déplacement du centre d'inertie G par rapport à la position d'équilibre. M : masse de l'équipage mobile ( M= 6,6 10-3 kg) Fe : force élastique résultant de l'action des deux ressorts, qui a pour direction l'axe x'x et pour valeur algébrique Fe = -kx avec k= 438 N/m f : force de frottement fluide exercée par l'air f= fx= -rdx/dt avec r= 0,52 kg s-1. Fm : force magnétique créee par le courant dans la bobine, lors du fonctionnement du haut parleur. L'intensité variable du courant est de la forme i(t) = Imax sin ( 2pft)
corrigé A position d'équilibre, origine de l'axe :
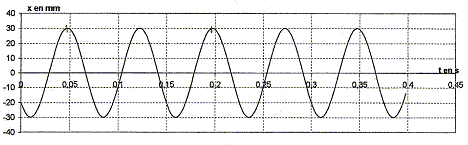
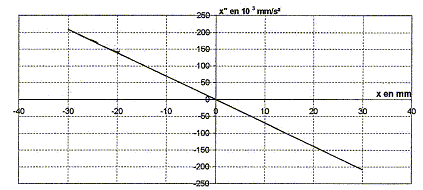
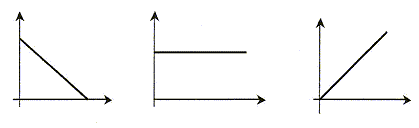
longueur de R1 : l1+x = l0+L+x ; allongement : L+x longueur de R2 : l2-x = l0+ L-x ; allongement : L-x la seconde loi de Newton s'écrit en projection sur l'axe Ax : -T1 + T2 = mx" -k(L+x) + k(L-x)=mx" 2kx=mx" soit x" + 2k/m x=0 ; on pose w²= 2k/m ; w = 2pf soit f = 1/(2p)[2k/m]½ ; T0= 1/f = 2p[2k/m]-½ solution de l'équation différentielle : x(t) = Xm cos ( 2pt/T0+F) ; x'(t) = -Xm 2p/T0sin ( 2pt/T0+F) ; x"(t) = -Xm(2p/T0)² cos ( 2pt/T0+F) repport dans l'équation différentielle : -Xm(2p/T0)² cos ( 2pt/T0+F) +2k/m Xm cos ( 2pt/T0+F) =0 vérifiée quel que soit t si : (2p/T0)² = 2k/m soit T0= 1/f = 2p[m/(2k)]½ Détermination graphique de la période T0 et l'amplitude : 4 périodes correspondent à 0,3 s d'où T0 = 0,075 s. Amplitude : 30 mm = 0,03 m valeur approchée de la constante de raideur k : k= ½(2p/T0)² m = 0,5*4 p ² *6,24 10-2 / (7,5 10-2)² = 2 p ²*624/ 7,5² = 222 N/m. représentation graphique des couples de points (x, x") : équation différentielle : x" + w² x=0 soit x" = - w² x, droite de coefficient directeur - w². w² = 200 103 / 29 = 2 105/29 =6896 ; or w² = 2k/m soit k = 0,5 *0,0624*2 105/29 = 6240/29 = 215 N/m. expression de l'énergie mécanique E : énergie potentielle élastique : ½(2k)x² ; énergie cinétique : ½mv²=½mx'² ; énergie mécanique : E= ½(2k)x² + ½mx'² conservation de l'énergie : E= ½(2k)x² + ½mx'² ; x² + m/(2k) x'² =E/k ; (x'/w)²+x²=E/k = C expression de C en fonction de l'amplitude Xm : si x=Xm l'énergie mécanique est entièrement sous forme d'énergie potentielle élastique E= ½(2k) Xm² d'où C= Xm² = 9 10-4 m². A partir de l'expression de E, retrouver l'équation différentielle : E= ½(2k)x² + ½mx'² ; dériver par rapport au temps : 0 =2k x x' + mx' x" ; 2kx+mx"=0 ; x"+2k/m x=0 représentations graphiques des couples (t,E) ou (x²,(x'/w)²) : le second graphique correspond à E=f(t) = constante ( droite horizontale). le premier graphique correspond à (x'/w)² = C-x² ; (x'/w)² =f(x²) fonction affine
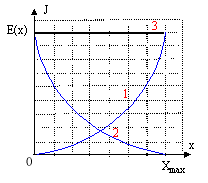
décroissante. Epe(x)= ½(2k) x² d'où Ec(x) = E(x)-Epe(x)=k( Xmax²-x²)
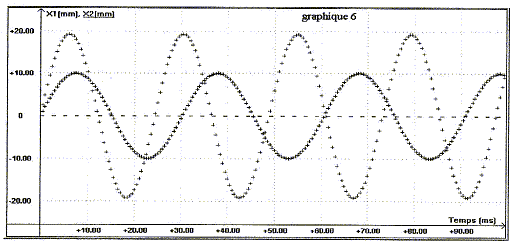
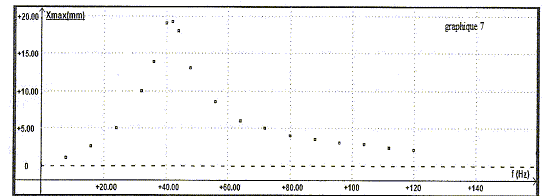
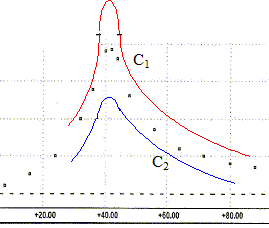
(1) énergie potentielle ; (2) énergie cinétique ; (3) énergie mécanique. ordre de grandeur du pourcentage de l'énergie perdue par l'oscillateur en une période : en 4 périodes, l'amplitude passe de 3 cm à 0,5 cm l'énergie mécanique est proportionnelle au carré de l'amplitude : DE est proportionnelle à (3²-0,5²)= 8,75 soit 8,75/9*100 = 97% soit 97/4 = 24% à chaque période. relation numérique entre la valeur Fm de la force magnétique et l'allongement du ressort : à l'équilibre du ressort, la force magnétique et la tension du ressort se neutralisent : ces deux forces ont même valeur ; Fm=kx , x étant l'allongement du ressort. relation numérique liant Fm et l'intensité du courant I : d'après le graphe 5, l'allongement x et l'intensité I sont proportionnels : x= 14,7 10-3 I ( x en m et I en A) d'où Fm = 14,710-3 kI = 14,710-3*438 I = 6,44 I. type d'oscillations que subit la membrane du haut-parleur : oscillations forcées. équation différentielle : L'équipage mobile est soumis à : son poids, opposé à l'action du support ( guide) à la position d'équilibre ; - la force élastique résultant de l'action des deux ressorts, qui a pour direction l'axe x'x et pour valeur algébrique Fe = -438x - la force de frottement fluide exercée par l'air f= fx= -r dx/dt = - 0,52 x' - la force magnétique créee par le courant dans la bobine, lors du fonctionnement du haut parleur Fm = 6,44 Imax sin ( 2pft) Ecrire la seconde loi de Newton sur un axe horizontal : Mx" = -438x - 0,52 x'+6,44 Imax sin ( 2pft) d'où : 6,6 10-3 x" + 0,52 x'+438x= 6,44 Imax sin ( 2pft) commentaires sur les courbes graphe 6 : f=f0= 41 Hz correspond à la fréquence propre de l'oscillateur ( d'après le graphe 7). L'amplitude est de l'ordre de 20 mm ; lorsque la fréquence de l'excitateur est voisine de la fréquence propre du résonateur, on observe un phénomène de résonance. Pour les autres fréquences de l'excitateur ( f= 33 Hz par exemple) , on observera une amplitude plus faible. La fréquence f0 correspondant au
maximum est la fréquence propre du résonateur. - si les frottements sont augmentés ( C2) : amplitude plus faible à la résonance, voir plus de résponance du tout.
|
||
|
|