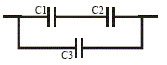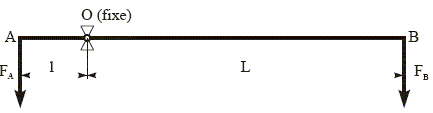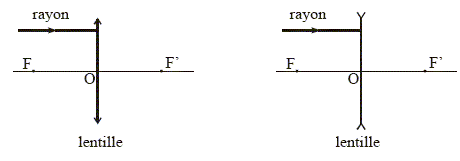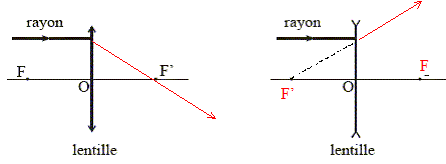|
( université Claude Bernard Lyon 1 ) ITRF 2003 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
||||||||||||||||||
| .
. |
||||||||||||||||||
|
||||||||||||||||||
|
|
corrigé intensité maximale Imax qui peut traverser cette résistance : P= R I² d'où I=[P/R]½ avec R = 1000 W ; P = 1 W Imax=[1/1000]½ =3,16 10-2 A = 31,6 mA. si cette résistance est parcourue par une intensité I telle que I = 2 Imax, la résistance sera détériorée. Fusible choisi pour une protection optimale de ce moteur : P= UI soit I= P/U avec P = 500 W ; U = 230 V (monophasé) Imax= 500/230 = 2,2 A
donc fusible
rapide 2 A.
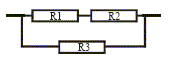
R1+R2 et R3 en dérivation équivalent à : Réqui= ( R1+R2 )R3 / (R1+R2+ R3) Réqui=
30*30 / 60 = 15
kW.
C1C2 / (C1+C2) et C3 en dérivation, équivalent à : Céqui= C1C2 / (C1+C2) + C3. Céqui= 1*2/3 +3 = 3,67 mF. (1) :
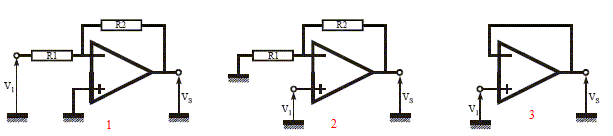
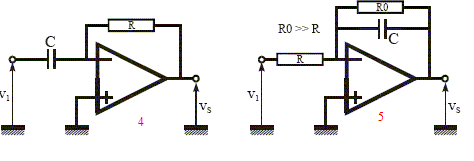
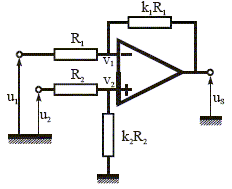
amplificateur inverseur ; (2) : amplificateur non inverseur ; (3 )
suiveur ; (4) : dérivateur ; (5) : intégrateur.
on note i l'intensité traversant R1 et k1R1 ; i' celle traversant R2 et k2R2 ; k=k1+1 et k'=k2+1 additivité des tensions : U2 = R2k' i' soit i' = U 2 /( R2k') Us+R1k i= U 1+R1k i soit i = (Us- U 1)/(R1k) U 2 - U 1 = R2 i' - R1i remplacer i et i' par leur expressions d'où : U 2 - U 1 = R2U2 /( R2k') + R1(Us- U 1)/(R1k) mumtiplier les deux membres par R2k'R1k : (U 2 - U 1)R2R1k k' =R2R1kU2+ R1R2k'(Us- U 1) (U 2 - U 1)k k' = kU2+ k'(Us- U 1) k(k'-1)U2 -k'(k-1)U1 = k' Us. or U1 = Uc-½Ud et U2= Uc+½Ud . k(k'-1)(Uc+½Ud )-k'(k-1)(Uc-½Ud)= k' Us. (k'-k)Uc+½(2kk'-k-k')Ud = k' Us. Us = (1-k/k')Uc+½(2k-1-k/k')Ud ; de la forme uS = Ad.ud + AC.uC avec AC.= 1-k/k' = 1-(k1+1 )/(k2+1) et Ad. = ½[2k1+1- (k1+1 )/(k2+1)] si k=k' alors Us = k1 Ud.
|
|||||||||||||||||
|
corrigé à l’équilibre du bras de levier : FAl = FB L FA=FB L/l = 10*2/0,2 = 100 N. masse M que l'on pourrait
soulever en A : FA/ g = 100 /9,8 =10,2 kg.
k =12/(0,3-0,15) = 12/0,15 =80 N /m . Pour doubler la raideur de ce ressort, on pourrait en associer deux en parallèle ; k= bGd4/(D3n) G ; dépend du matériau , d : diamètre du fil ; D : diamètre d'une spire ; n : nombre de spires actives On pourrait aussi augmenter le diamètre du fil, diminuer le diamètre de l'enroulement, diviser par deux le nombre de spires actives.
Le véhicule est soumis à son poids, vertical , vers le bas, valeur Mg et à l'action du plan , perpendiculaire au plan. Ecrire la seconde loi de Newton sur un axe parallèle au plan, orienté vers le bas : d'où Mg sin a = Mg soit g=
g sina
avec sina
voisin de 0,1 ;g
= 0,98 m/s².
puissance (W) = force (N) fois vitesse (m/s) vitesse =P/ (Mg) = 1000 /(1000*9,8) = 1/9,8 = 0,10 m/s. |
||||||||||||||||||
corrigé refroidissement le plus efficace pour un même montage : circulation d’eau par ordre de conductivités thermiques
croissantes : cuivre, aluminium, acier, bois, laine de verre.
énergie gagnée par le calorimètre et l'eau qu'il contient : (m1+m)c1(q -q1 ) énergie cédée par l'aluminium : m2c2(q -q2 ) système adiabatique : (m1+m)c1(q -q1 ) + m2c2(q -q2 ) = 0 (m1+m) c1q -(m1+m)c1q1 +m2c2q - m2c2q2 = 0 ; ((m1+m)c1 + m2c2)q = m2c2q2+(m1+m)c1q1 ; q = [m2c2q2+(m1+m)c1q1 ] / [(m1+m)c1 + m2c2] si m négligeable : q =[0,1*896*100+0,27*4185*19) / ( 0,27*4185+0,1*896) = 25°C. si m non négligeable : q ' =[0,1*896*100+0,3*4185*19) / ( 0,3*4185+0,1*896) = 24,4°C.
La grandeur électrique délivrée par le capteur est une résistance R. La caractéristique de transfert, donnée par le constructeur s'exprime par : R= 100+0,385 q ( q en °C) Les variations de la valeur de la résistance
entraînent des modifications du courant ou de la tension dans un
circuit extérieur alimenté par une source de tension. Il faut amplifier
ces faibles modifications.
les thermocouples mesurent une différence de température. Deux métaux, de natures différentes, sont reliés par deux jonctions (ils constituent ainsi un thermocouple) placées aux températures T1 et T2. Par effet Seebeck, la différence de température entre les jonctions, entraîne une différence de potentiel Il est donc nécessaire de connaître la relation entre la différence de potentiel et la différence de température
|
||||||||||||||||||
corrigé ordre de grandeur de la vitesse de la lumière dans le vide : 3 108 m/s lumière monochromatique : une seule couleur, une seule fréquence. un exemple de source monochromatique : laser
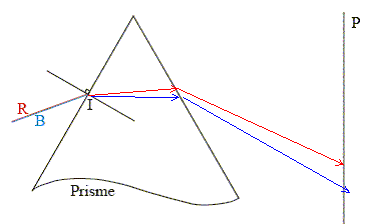
lentille achromatique : Une lentille dévie de manière différentes les radiations lumineuses ayant des longueurs d'onde différentes ; les images obtenues en lumière blanche sont irrisées de bleu ou de rouge . On appelle cela" aberration chromatique ". Une lentille achromatique est une combinaison judicieuse de lentilles conduisant à des aberrations chromatiques les plus faibles possibles.
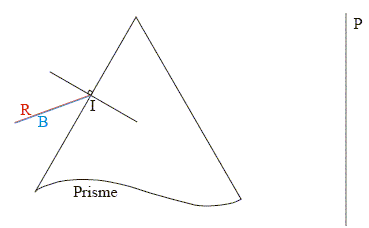
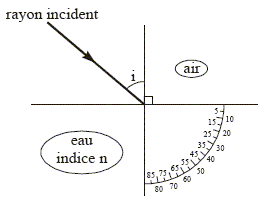
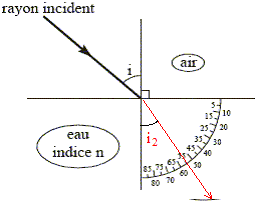
loi de Descartes pour la réfration : nair sin i = n sin i2 ; sin i2 = nair sin i / n = 1*sin49,43 / 1,33 =0,571 ; i2 = 34,8°.
|
||||||||||||||||||
corrigé onde sonore, une onde ultrasonore : onde mécanique longitudinale ; propagation d'une variation de pression à la célérité v, avec transport d'énergie, sans transport de matière. Les fréquences associées à une onde sonore sont comprise entre 20 Hz et 20 000 Hz ; les fréquences des ultrasons sont supérieures à 20 000 Hz. Dans l'air les longueurs d'onde correspondantes sont comprises entre : l=v/f 330/20 = 16,5 m et 330/20000 = 1,65 10-2 m. distance L séparant la personne et l’obstacle : d'une part distance (m) = vitesse (m/s) * temps (s) ; d'autre part durée de l'aller + retour = 2 s ; d'où : L= 330*1 = 330 m.
résultante des forces de pression F : F (N) = S( m²) * p (pa) d= 200 mm = 0,2 m ; r = ½d = 0,1 m ; surface S= p r² = 3,14*0,1² = 3,14 10-2 m² force due à l'air extérieur, dirigée vers l'intérieur de l'enceinte, perpendiculaire à la surface, valeur : 3,14 10-2 * 105 = 3,14 103 N force due à l'air intérieur, dirigée vers l'extérieur de l'enceinte, perpendiculaire à la surface, valeur : 3,14 10-2 * 102 = 3,14 N d'où F= 3,14 103 -3,14
voisin 3,136 103
N.
Le vide secondaire ( 1 à 10-7 hPa) est obtenu à l'aide de pompe turbomoléculaire, de pompe à diffusion d’huile.
|
||||||||||||||||||
corrigé acide ( définition de Brönsted) : espèce, ion ou molécule susceptible de céder un proton H+. base : espèce, ion ou molécule susceptible de gagner un proton H+. NaCl : chlorure de sodium M= 58,5 g/mol ; H2O : eau M= 18 g/mol ; H2SO4 : acide sulfurique M= 98 g/mol; HCl : chlorure d'hydrogène M = 36,5 g/mol ; CO2 :dioxyde de carbone M = 44 g/mol ; NaOH : hydroxyde de sodium ou soude M=40 g/mol. dangers principaux de l’azote liquide : gel des tissus humains (les yeux, la peau), la fragilisation des aciers et le durcissement des plastiques. Port de gants de cuir, de lunettes et de chaussures de protection. principal danger d’un laser de faible puissance : l'oeil est l'organe le plus fragile : la rétine peut être endomagée même avec des lasers de faible puissance ( 1mW) : port de lunettes spéciales.
|
||||||||||||||||||
|
|
||||||||||||||||||