Etude d'une éolienne : l'hélice concours physique Capes 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

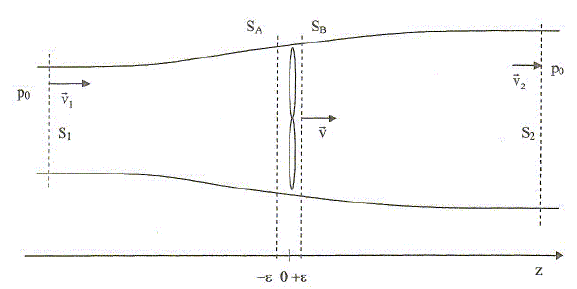
Fonctionnement de l'hélice : On fait les hypothèses suivantes : - On effectue l'étude dans un référentiel R lié au sol et supposé galiléen - l'air est considéré comme un fluide parfait, homogène et incompressible de masse volumique µ - on suppose le mouvement de l'air stationnaire et à symétrie de révolution autour de l'axe de rotation de l'hélice - la pression à grande distance de l'hélice est uniforme et égale à la pression atmosphérique notée p0. - la pression garde la même valeur sur une section droite du tube de courant du champ des vitesses - les sections SA et SB du tube de courant sont égales à S et on note la pression pA sur SA et pB sur SB - On néglige les effets de la pesanteur - l'écoulement étant turbulent au niveau de l'hélice, on admet pour simplifier que la vitesse v de l'air est la même en z = -e, en z=0 et en z = +e. Ecrire la conservation du débit massique DM à travers diverses sections droites du tube de courant et en déduire deux relations entre S1, S2, S,v , v1 et v2. On note DV(m3 s-1) le débit volumique : DM = µ DV ; or le débit volumique est homogène à une section (m2) fois une vitesse (m s-1), d'où : DM = µ DV = µ S v. La conservation du débit massique conduit à : µ S v =µ S1 v1= µ S2 v2 soit : S v= S1 v1= µ S2 v2. En utilisant le théorème de Bernoulli entre les section S1 et SA d'une part et entre les sections SB et S2 d'autre part, déduire l'expression de la pression pA en fonction de p0, µ, v1 et v, puis celle de pB en fonction de p0, µ, v2 et v. Expression du théorème de Bernoulli en régime stationnaire : p + ½µv2 + µgh = Cste. Les effets de la pesanteur étant négligés, le terme µgh est nul, d'où : p +½µv2=Cste. Entre les sections S1 et SA : p0+½µv12 = pA +½µv2 ; pA = p0+½µ(v12 -v2 ). Entre les sections S2 et SB : p0+½µv22 = pB +½µv2 ; pB = p0+½µ(v22 -v2 ). Les vecteurs sont écrits en gras et en bleu. En effectuant un bilan de quantité de mouvement pour le fluide compris entre les sections SA et SB, établir que la force F exercée par l'air sur l'hélice s'écrit : F = ½µS( v12 - v22 )ez où ez est le vecteur unitaire de l'axe z. Commenter. 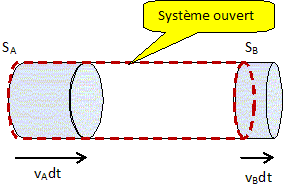Le cylindre en pointillé brun constitue un système ouvert ; le cylindre central blanc est un système fermé. Le mouvement de l'air étant stationnaire : P système ouvert (t+dt) -P système ouvert (t) = 0. P système fermé (t+dt) -P système fermé (t) = dP sortant-dPentrant. dP sortant= dMsortantvB = µ S vB vB ; dP entrant = dMentrantvA = µ S vA vA. Théorème de la résultante dynamique appliqué au système fermé : SFextérieures = Mdv/dt = d P système fermé /dt = µ S[vB vB -vA vA] = µ S[v v -v v] =0. Bilan des forces extérieures : ( les forces de pesanteurs sont négligées) - Forces pressantes sur les sections droites du cylindre : pASAez - pBSBez= pASez - pBSez=( pA - pB)Sez la résultante de ces mêmes forces sur la paroi latérale est nulle. - Force exercée par l'éolienne sur l'air -F. Par suite :( pA - pB)Sez- F = µ S[vB vB -vA vA] =0. Or pA = p0+½µ(v12 -v2 ) et pB = p0+½µ(v22 -v2 ) ; pA - pB = ½µ(v12 -v22 ) F =½µ(v12 -v22 )Sez. Cette force est proportionnelle à la différence des carrés des vitesses amont et aval du vent : l'éolienne doit être capable de prendre le maximum de l'énergie cinétique du vent. A l'aide d'un bilan pour le fluide compris entre les sections S1 et S2, établir une autre relation entre F, DM, v1, v2 et ez. Même méthode appliquée au tube de courant fermé s'appuyant sur les sections S1 et S2. La pression p0 est la même sur le tube de courant : la résultante des forces de pression est nulle. d'où µ [S2v2 v2 -S1v1 v1] = -F ; or DM = µ DV = µ S v = µS2v2 =µS1v1. F = µ DV (v1-v2) = µ DV (v1- v2) ez. En déduire que la vitesse v de l'air au niveau de l'éolienne s'écrit : v = ½(v1+v2) D'une part : F =½µ(v12 -v22 )Sez. ; d'autre part : F = µ DV (v1- v2) ez. d'où : ½(v1+v2)S = DV = S v ; v = ½(v1+v2) Evaluer la puissance P reçue par l'hélice en fonction de µ, S, v1 et x= v2 / v1. Le fluide est parfait : il n'y a pas de puissance mécanique perdue. Puissance recue par l'hélice de la part du fluide : F. v =µ DV (v1- v2) v ez.ez = µ DV (v1- v2) v =½ µ DV (v1- v2)(v1+v2) P = ½ µ DV v21 (1-x)(1+x) = ½ µ S1 v31 (1-x)(1+x) or S v = S1 v1 ; S1 = S v /v1 =½S(1+x) ; par suite : P =0,25 µ S v31 (1-x)(1+x)2. 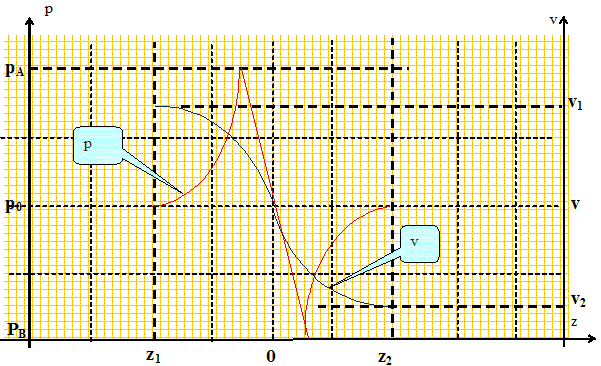Loi de Betz : la vitesse de l'air après l'éolienne ne pouvant pas s'annuler, il existe une puissance maximale Pmax que l'on peut extraire de la circulation de l'air. Pour quelle valeur de x la puissance est-elle maximale ? Donner la valeur de Pmax. Dériver P par rapport à x puis chercher la valeur de x qui annule cette dérivée : 0 = 0,25 µ S v31 [ -(1+x)2+2(1+x)(1-x)] ; -(1+x)+2(1-x) =0 ; x = 1/3 ; Pmax =0,25 µ S v31 [2/3*16/9] =8/27µ S v31. Tracer l'allure des courbes vitesse v(z) et pression p(z) sur le même graphique. Commenter. pA = p0+½µ(v12 -v2 ) ; p +½µv2=Cste On observe deux effets antagonistes : Le fluide se déplace du fait de la différence de pression pA - pB = ½µ(v12 -v22 ) ; plus la vitesse v2 est faible, plus la différence de pression pA - pB est grande. Or v = ½(v1+v2) : si la vitesse v2 diminue alors la vitesse v est plus faible. Le rendement de l'éolienne est défini comme le rapport de la puissance P fournie par l'air à l'hélice sur le débit d'énergie cinétique en amont de l'éolienne : rth = P/Ec. Calculer le débit d'énergie cinétique DEc à travers la section droite de surface S où la vitesse est v1. En déduire le rendement théorique de l'éolienne en fonction de x. Energie cinétique élémentaire dEc portée par le volume élémentaire cylindrique de section S et de hauteur v1dt : masse correspondant au volume Sv1dt : µSv1dt dEc = ½µSv1dt v21 = ½µS v31 dt d'où : DEc = dEc /dt = ½µS v31. P =0,25 µ S v31 (1-x)(1+x)2 ; rthéo =P / DEc =½(1-x)(1+x)2. A.N : µ=1,3 kg m-3 ; v1 = 12 m s-1 ; S= 1,4 m2. Calculer Pmax et le rendement associé. Pmax =8/27µ S v31 = 8/27*1,3*1,4*123 =9,3 102 W. rendement : 0,5*2/3*(1+1/3)2 =16/27 = 0,59. A cause des turbulences au niveau des pale, le rendement est plus faible et la puissance peut s'écrire : Préelle =½CpµSv31 où Cp est le coefficient de performance. Il dépend de la féométrie, de l'inclinaison des pales et de la vitesse du vent. Montrer que Cp admet une valeur maximale à cause de la loi de Betz. Pthéorique =0,25 µ S v31 (1-x)(1+x)2 ; Préelle =½CpµSv31 Or Pthéorique > Préelle d'où ½(1-x)(1+x)2 > Cp. et en remplaçant x par 1/3 ( puissance maximale) : Cp <16/27. Calculer Cp pour une puissance réelle de 400 W. Cp = 2Préelle /(µSv31) =800 /(1,3*1,4*123) = 0,25.

retour -menu