Aurélie novembre 2000

. .
mouvement d'une bille sur un dôme sphérique

d'après concours Kiné Assas

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.


 
1

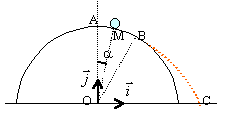
étude du trajet AB
Un petit solide considéré comme ponctuel, de masse m, est abandonné sans vitesse depuis A, sommet d'une hémisphère de rayon r. Sur le parcours AB, la bille reste en contact avec la surface de l'hémisphère. Au point B, la bille perd le contact et suit la trajectoire BC.
  1. Représenter les forces qui s'exercent sur la bille en un point M du trajet AB.
  2. Exprimer l'intensité R de l'action du plan sur la bille en fonction de m, g, r, v et a.
  3. En utilisant le théorème de l'énergie cinétique exprimer le module de la vitesse de la bille en M en fonction de g, r et a.
  4. Lors de la perte de contact en B, quelle valeur prend l'intensité R de la réaction du plan sur la bille ?
  5. Quelles sont en B les valeurs a0 et v0 de a et de la vitesse ?
 

corrigé


 

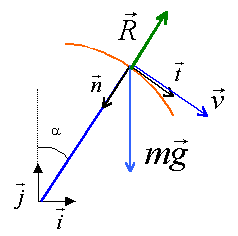
expression de la vitesse en M :

origine des altitudes , le point O. Ecrire la conservation de l'énergie mécanique.

mgOA = mgOAcos a + 0,5 m vM²

vM²= 2gOA(1-cos a )

expression de l'action du support en M :

th du centre d'inertie projeté sur le vecteur n de la base de Frenet.

-R + mgcos a = m v²M / OA

remplacer vM²par 2gOA(1-cos a )

R= mg(3cos a -2)

en B plus de contact avec le support donc R=0

3cos a = 2 --> a0 = 48,18 °

v²B=2*9,8*(1-cos48,18)= 6,53

v0=2,55 ms-1.
2

étude du trajet BC
  1. Quelle est la nature du mouvement de la bille sur le trajet BC ?
  2. Donner les équations horaires du mouvement de la bille dans le repère indiqué en fonction de g, a0 et v0. L'origine des temps est prise au moment où la bille perd le contact du plan.
  3. Calculer l'abscisse du point C, point d'impact avec le sol

    Données g=9,8 m s-2 r=1 m et m=0,1 kg.

     

corrigé


 chute libre avec vitesse initiale

conditions initiales :

vitesse à la date t :

vecteur position à la date t :

application numérique :

x=1,7 t + 0,745

y= -4,9 t²-1,9 t + 0,667

trajectoire :

(poser X= x-0,745 pour simplifier l'écriture)

y=-1,695 X²-1,117 X+0,667.

point d'impact yC=0

résoudre l'équation du second degré :

-1,695 X²-1,117 X+ 0,667=0

discriminant D= 1,117² + 4*0,667*1,695 =5,77

X1=-1,037

X2=0,378-->x = 1,123 m.

retour - menu