Mathématiques, Brevet des collèges Pondichéry 2012 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Exercice 1.  Un ouvrier dispose de plaques de métal de 110 cm de longueur et de 88 cm de largeur. Il a reçu la consigne suivante : «Découpe dans ces plaques des carrés tous identiques, dont les longueurs des côtés sont un nombre entier de cm, et de façon à ne pas avoir de perte. » 1. Peut-il choisir de découper des plaques de 10 cm de côté ? Justifier votre réponse. Non, car 88 n'est pas un multiple de 10. 2. Peut-il choisir de découper des plaques de 11 cm de côté ? Justifier votre réponse. Oui, car 11 est un diviseur à la fois de 110 et de 88. 3. On lui impose désormais de découper des carrés les plus grands possibles. a. Quelle sera la longueur du côté d’un carré ? Algorithme d'Euclide :110 =88 +22 ; 88 =4 x22. Le PGCD de 110 et 88 est égal à 22. Les plus grands carrés ont un côté de 22 cm. b. Combien y aura-t-il de carrés par plaques ? 88 /22 =4 ; 110 / 22 =5 ; il y a 4 x5 = 20 carrés par plaques. . . Exercice 2. La note de restaurant suivante est partiellement effacée. Retrouvez les éléments manquants ; en présentant les calculs effectués RESTAURANT « la Gavotte » 4 menus à 16,50 € l’unité . . . . . . 1 bouteille d’eau minérale . . . . . . 3 cafés à 1,20 € l’unité . . . . . . Sous total . . . . . . Service 5,5 % du sous total 4,18 € Total ..... Le sous-total est égal à : 4,18 / 5,5 x100=76 €. Total : 4,18 +76 = 80,18 €. Café : 3 x1,20 = 3,60 €. Menus : 4 x16,50 = 66 €. Eau minérale : 76-66-3,60 =6,4 €. ... Exercice 3. Dans un pot au couvercle rouge on a mis 6 bonbons à la fraise et 10 bonbons à la menthe. Dans un pot au couvercle bleu on a mis 8 bonbons à la fraise et 14 bonbons à la menthe. Les bonbons sont enveloppés de telle façon qu’on ne peut pas les différencier. Antoine préfère les bonbons à la fraise. Dans quel pot a-t-il le plus de chance de choisir un bonbon à la fraise ? Justifier votre réponse.. Couvercle rouge : 6 cas favorables sur 16 cas possibles ; probabilité de tirer un bonbon à la fraise : 6 / 16 = 3 /8 =0,375. Couvercle bleu : 8 cas favorables sur 22 cas possibles ; probabilité de tirer un bonbon à la fraise : 8 / 22 = 4 /11 =0,364. Le pot au couvercle rouge donne le plus de chance de tirer un bonbon à la fraise. Exercice 4. Un jeune berger se trouve au bord d’un puits de forme cylindrique dont le diamètre vaut 75 cm : il aligne son regard avec le bord inférieur du puits et le fond du puits pour en estimer la profondeur. Le fond du puits et le rebord sont horizontaux. Le puits est vertical. 1. En s’aidant du  schéma ci-dessous (il n’est pas à l’échelle), donner les longueurs CB, FG, RB en mètres Cb = 0,20 m ; FG = 0,75 +0,20 = 0,95 m ; RB = 0,80 m. 2. Calculer la profondeur BG du puits. 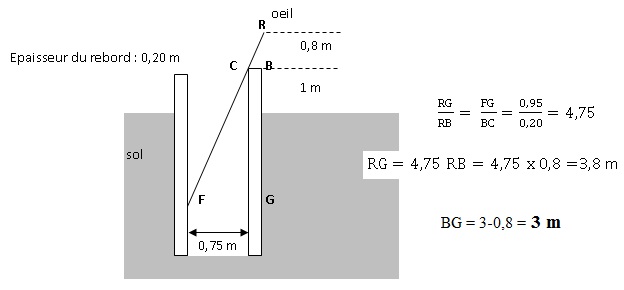3. Le berger s’aperçoit que la hauteur d’eau dans le puits est 2,60 m. Le jeune berger a besoin de 1m3 d’eau pour abreuver tous ses moutons. En trouvera-t-il suffisamment dans ce puits ? Volume d'eau : p r2 h = 3,14 x0,3752 x2,6 ~1,15 m3. Il trouve suffisamment d'eau. . . Exercice 5. Voici la figure à main levée d’un quadrilatère.: 1. Reproduire en vraie grandeur ce quadrilatère.   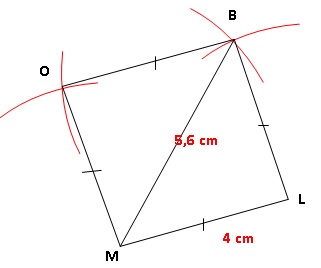2. Pourquoi peut-on affirmer que OELM est un losange ? Les 4 côtés du quadrilatère sont égaux. 3. Marie soutient que OELM est un carré, mais Charlotte est sûre que ce n’est pas vrai. Qui a raison? Pourquoi ? MB2 = 5,62 = 31,36. ML2 +BL2 = 42+42 = 32, différent de MB2. Le triangle BML n'est pas rectangle en L ; le quadrilatère n'est pas un carré. Exercice 6. Rémy dispose de 96 m de grillage avec lesquels il souhaite construire un enclos pour son poney. Il cherche quelle forme donner à son enclos pour que celui-ci ait la plus grande surface possible. Partie 1. Sa première idée est de réaliser un rectangle avec les 96 mde grillage. Calculer la longueur et la largeur de ce rectangle sachant que : - la longueur est le double de la largeur. - son périmètre est 96 m. Calculer l’aire de ce rectangle de 96 m de périmètre. On note x la longueur ; la largeur vaut 0,5 x ; le périmètre s'acrit : 2(x+0,5x) = 3x = 96 ; x = 32 ; Aire du rectangle = longueur x largeur = 32 x16 = 512 m2. Partie 2. Sa deuxième idée est de réaliser un carré. Calculer l’aire d’un carré de 96 m de périmètre. Côté du carré : 96 / 4 = 24 m ; aire du carré : 24 x24 = 576 m2. Partie 3. Sa troisième idée est de réaliser un hexagone régulier. Le schéma à main levée ci-contre représente un hexagone régulier ABCDEF de 96 m de périmètre. Il est inscrit dans un cercle de centre 0 et de rayon 16 m. Le segment [OH] est une hauteur du triangle équilatéral OBA. 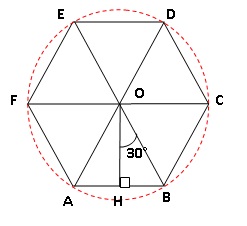1. Calculer la longueur OH, exprimée en m. En donner l’arrondi au centimètre près. OA = OB : le triangle AOB est isocèle en O. L'angle AOB mesure 360 / 6 = 60°. Le triangle OAB est équilatéral. La hauteur OH est également médiatrice du côté AB. cos 30 = OH / OB ; OH = OB cos 30 = 16 cos 30 = 16 x0,866 ~13,86 m. 2. Utiliser ce résultat pour calculer l’aire du triangle OBA, exprimée en m2 et arrondi au 1/10. OH x AB / 2 = 13,86 x16 / 2 = 110,85 ~110,9 m2. 3. En déduire l’arrondi à l’unité de l’aire d’un hexagone régulier de 96 m de périmètre. 6 x110,85 = 665,1 m2. Sa quatrième idée est de réaliser un octogone régulier de 96 m de périmètre. La figure suivante représente le plan réalisé par Rémy. Cet octogone est inscrit dans un cercle de centre I. Le segment [IK] est une hauteur du triangle isocèle IMN. 1. Vérifier que MN = 12 m dans la réalité. 96 / 8 = 12 m. 2. En prenant pour échelle 1 cm pour 3 m, représenter le triangle IMN, puis le point K. Laisser apparents tous les traits de construction. 3. Mesurer sur votre plan la longueur IK. Combien de mètres cela représente-t-il dans la réalité ? 4,8 x 300 ~ 14,5 m. 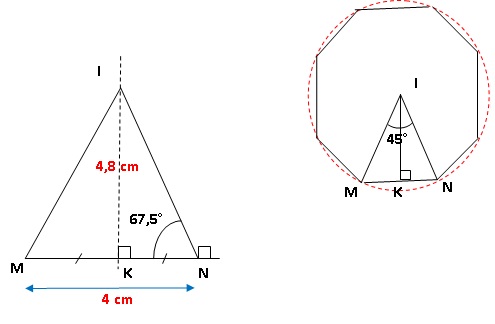4. En déduire l’aire du triangle MIN, puis, à partir de cette valeur, calculer l’aire d’un octogone régulier de 96 m de périmètre. Aire du triangle IMN : MN x IK / 2 = 12 x 14,5 / 2 =86,9 m2. Aire de l'octogone régulier : 8 x 86,9 ~ 595,3 m2. Les recherches ont permis à Rémy de remarquer que l’aire d’un polygone régulier de 96 m de périmètre semble augmenter quand on augmente le nombre de ses côtés. Il imagine qu’un enclos circulaire aurait peut-être une surface encore plus grande. 1. Quel rayon faut-il prendre pour avoir un disque de périmètre 96 m ? 2 p r = 96 ; r = 96 /(2p) ~ 15,3 m. 2. En déduire l’aire d’un disque ayant pour périmètre 96 m. pr2 = 3,14 x15,32 ~733 m2.

menu