Mathématiques, Brevet des collèges Asie 2012

Mathématiques, Brevet des collèges Asie 2012

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
Le tableau ci-dessous a été construit en comptant les fréquences des 26 lettres de l’alphabet dans un texte français de 100 000 lettres composé de textes de Gustave Flaubert, de Jules Verne et de trois articles de l’Encyclopedia Universalis.

Lettre
A
B
C
D
E
F
G
H
I
J
K
L
M

Fréquence (%)
8,4
1,06
3,03
4,18
17,26
1,12
1,27
0,92
7,35
0,31
0,05
6,01
2,96

Lettre
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

Fréquence (%)
7,13
5,26
3,01
0,99
6,55
8.08
7,07
5,74
1,32
0,04
0,47
0,30
0,12

1. Quelles sont les cinq lettres les plus fréquentes ? E, A, S, I, N.
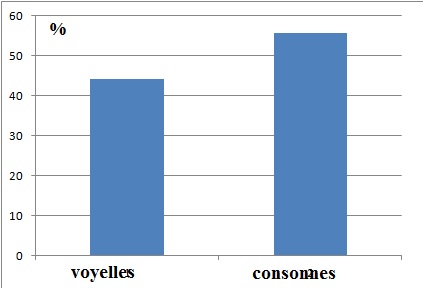
2. Représenter graphiquement la répartition des voyelles et des consonnes.
Nombre de voyelles : 1000 (8,4 +17,26 +7,35 +5,26 +5,74+0,30) =44310 ( 44,3 %)
nombre de consonnes 100 000 -44310 = 55690 ( 55,7 %).

3. Si toutes les lettres avaient la même fréquence d’apparition, quelle serait cette fréquence ?
1 / 26 = 0,0385 ou 3,85 %.

.
.

Exercice 2.
Dans un jeu de société, les jetons sont des supports de format carré, de mêmes couleurs,
sur lesquels une lettre de l’alphabet est inscrite. Le revers n’est pas identifiable.
Il y a 100 jetons. Le tableau ci-dessous donne le nombre de jetons du jeu pour chacune des voyelles

Lettres du jeu
A
E
I
O
U
Y

Effectif
9
15
8
6
6
1

On choisit au hasard une lettre de ce jeu.
1. Quelle est la probabilité d’obtenir la lettre I ?
8 cas favorables sur 100 possibles ; 8 / 100 = 0,08.
2. Quelle est la probabilité d’obtenir une voyelle ?
Le jeu compte 45 voyelles sur 100 jetons : 0,45.
3. Quelle est la probabilité d’obtenir une consonne ?
1-0,45 = 0,55.

Exercice 3.
On considère la fonction f définie par : f (x) = −5x +1
1. Calculer l’image de −3 par f .
f(-3) = -5 x(-3) +1 = 15+1 = 16.
2. Calculer l’antécédent de 4 par f .
4 = -5x+1 ; 5x = 1-4 = -3 ; x = -3/5 = -0,6.

Exercice 4. QCM.
1. Racine carrée (50) = racine carrée ( 2 x25) =racine carrée (2 x5²) = 5 x racine carrée (2). Réponse A.
2. Quel que soit x, on a : (2x-1)² = 4x² -4x+1. Réponse C.
3. Le PGCD de 91 et 119 est :
Algorithme d'Euclide : 119 = 91 +28 ; 91 = 28 x 3 +7 ; 28 = 7 x4.
Le PGCD de 119 et 91 est 7. Réponse B.

.
.

Exercice 5.
La terrasse est représentée par le segment [DN] elle est horizontale et mesure 4 mètres de longueur. Elle est construite au-dessus d’un terrain
en pente qui est représenté par le segment [DP] de longueur 4,20 m. Pour cela, il a fallu construire un mur vertical représenté par le segment [NP].

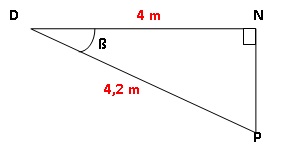
1. Quelle est la hauteur du mur ? Justifier. Donner l’arrondi au cm près.
NP² = DP²-DN² = 4,2² -4² = 1,64 ; NP = 1,28 m.
2. Calculer l’angle� ß compris entre la terrasse et le terrain en pente. (Donner l’arrondi au degré près)
cos ß = DN / DP = 4 / 4,2 ~0,952 ; ß = 17,75 ~18°.

Exercice 6.
Soit ADU un triangle représenté ci-dessous, F un point de [AD], C un point de [AU]. L’unité de longueur est le centimètre.
On donne AF = 3 ; FD = 1,5 ; AC = 2 ; AU = 3
Sur la figure, les dimensions ne sont pas respectées.
1. Démontrer que les droites (FC) et (DU) sont parallèles.

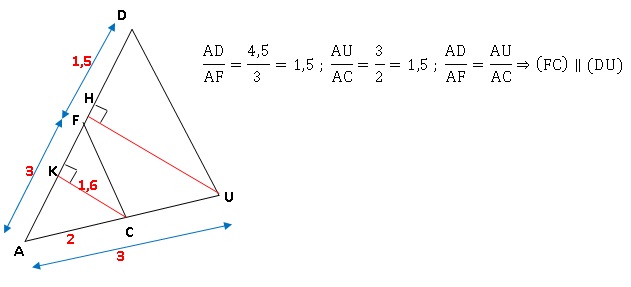
2. calculer l'aire du triangle ADU.
Pour passer du triangle AFC au triangle ADU, le coefficient multiplicateur est 1,5.
Donc UH = CK x1,5 = 1,6 x1,5 = 2,4 cm.
Aire du triangle ADU : HU x AD / 2 = 2,4 x4,5 / 2 = 5,4 cm².

Exercice 7.
Le parc vous accueille dans une entrée-billetterie : c’est un pavé droit à base carrée surmonté d’une coupole semi-sphérique, représenté ci-dessous.

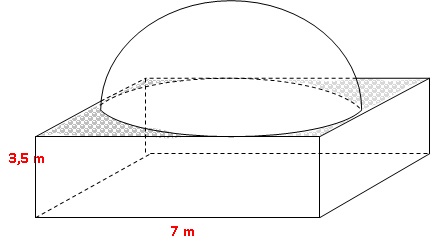
Partie 1 - Ouvert depuis quelques années, abîmé par les intempéries, ce bâtiment doit être repeint.
Toutes les surfaces extérieures sont repeintes, c’est-à-dire :
• les 4 faces latérales du pavé droit ;
• la partie plane du toit (parties grisées sur la figure) ;
• la coupole semi-sphérique.
1. Sachant que les ouvertures (portes et fenêtres, non représentées sur la figure) occupent une surface de 18 m²,montrer que l’aire totale des surfaces à peindre est d’environ 168 m².
Surface latérale du pavé droit : 4 x7 x3,5 = 98 m².
Aire hachurée :: 7 x7 - 3,14 x3,5² = 10,52 m².
Aire de la demi-sphère : 2 x3,14 x3,5² = 76,97 m².
Aire des surfaces à repeindre : 98 + 10,52 +76,97 -18 = 167,48 ~168 m².
2. Compléter la facture à l’aide des informations fournies ci-dessous :
• Un pot de 10 L de peinture permet de couvrir une surface de 40 m² ;
• Le coût d’un pot de 10 L de peinture est de 400 €;
• Un ouvrier peint une surface de 42 m² à l’heure.

Quantité
Désignation
Prix unitaire ( €)
Prix total (€)

5
pots d'antirouille
500,00
5 x500 = 2500

168 / 40 = 4,2 ( 5 )
pots de peintue
400,00
5 x400 = 2000

2 couches de peinture ( antirouille + peinture )
2 (168 / 42) = 8
heures main d'oeuvre
35,00
8 x35 =280

Total HT
4780

TVA 19,6 %
4780 x0,196 =936,88

Total TTC
4780+936,88 = 5716,88

Partie II -À l’entrée du parc d’ani-math-ion figurent les informations suivantes :
Entrée adulte : 12 € Ouvert de 9 h à 18 h
Entrée enfant : 7 € Dernières entrées à 17 h
Forfait famille (sur présentation du livret de famille) : 35 € Fermé le lundi.
1. Le forfait famille
a. Est-il intéressant pour un couple et leur enfant de 8 ans de prendre le forfait famille ?
Sans forfait : 12 x2 +7 =31 €.
Avec le forfait : 35 €. Il ne faut pas prendre ce forfait.
b. À partir de quel nombre d’enfants, un couple a-t-il intérêt à choisir le forfait famille ?
On note a le nombre d'enfants. 2 x12 + 7 a >35 ; 7a >35,24 ; 7a >11 ; a > 11/7 ; a > 2.
2. Au cours d’une journée, 89 forfaits famille ont été vendus pour 510 personnes.
a. Déterminer la recette correspondante.
89 x35 = 3115 €.
b. Quel est le prix moyen par personne ?
3115 / 510 = 6,11 €.
3. Au cours de cette même journée, 380 personnes n’ont pas utilisé le forfait famille pour une recette correspondante de 3 660 €. Déterminer le nombre d’entrées adultes et le nombre d’entrées enfants vendues lors de cette journée.
On note a le nombre d'enfants ; nombre d'adultes : 380-a ;
(380-a) x12 + 7 a = 3660 ; 4560 -12a + 7a =3660 ;
4560 -3660 = 5a ; 900 = 5 a ; a = 900 / 5 = 180 enfants et 200 adultes.

menu