Mathématiques, Brevet des collèges Métropole 2012

Mathématiques, Brevet des collèges Métropole 2012

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
1. 1. Alice participe à un jeu télévisé. Elle a devant elle trois portes fermées. Derrière l’une des portes, il y a une voiture ; derrière les autres, il n’y a rien. Alice doit choisir l’une de ces portes. Si elle choisit la porte derrière laquelle il y a la voiture, elle gagne cette voiture.
Alice choisit au hasard une porte. Quelle est la probabilité qu’elle gagne la voiture ?
1 cas favorable sur 3 possibles. la probabilité de gagner est 1 / 3 ~0,33.
2. S’il y a quatre portes au lieu de trois et toujours une seule voiture à gagner, comment évolue la probabilité qu’a Alice de gagner la voiture ?
1 cas favorable sur 4 possibles. la probabilité de gagner est 1 / 4 ~0,25 ; la probabilité diminue.

.
.

Exercice 2.
1. Quelle est l’écriture décimale du nombre A ?

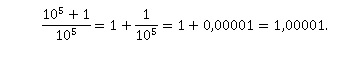2. Antoine utilise sa calculatrice pour calculer le nombre A, résultat affiché est 1.
Antoine pense que ce résultat n’est pas exact. A-t-il raison ?
Ce résultat est exact, la calculatrice a arrondi.

Exercice 3.
Lors d’un marathon, un coureur utilise sa montre-chronomètre. Après un kilomètre de course, elle lui indique qu’il court depuis quatre minutes et trente secondes. La longueur officielle d’un marathon est de 42,195 km. Si le coureur garde cette allure tout au long de sa course, mettra-t-il moins de 3 h 30 pour effectuer le marathon ?
1 km est parcouru en 4 x60 +30 = 270 s.
Pour parcourir 42,195 km, il mettra : 270 x 42,195 ~11392 s.
11392/ 3600 = 3,164 h ou 3 h et 0,164 x60 ~10 min.
Il terminera sa course en moins de 3 h 30 min en gardant cette allure.

Exercice 4.
On cherche à résoudre l’équation (4x −3)² −9 = 0.
1. Le nombre 3 / 4 est-il solution de cette équation? et le nombre 0 ?
4 x3 / 4 -3 = 3-3 = 0 ; (4x −3)² −9 =-9, différent de zéro.
4 /3 n'est pas solution de cette équation.
4 x0 / 4 -3 =-3 ; (-3)² = 9 ; (4x −3)² −9 = 9-9=0
0 est solution de cette équation.
2. Prouver que, pour tout nombre x, (4x −3)² −9 = 4x(4x −6).
Différence de deux carrés : (4x −3)² −3² =(4c-3+3)(4x-3-3)=4x(4x-6)
3. Déterminer les solutions de l’équation (4x −3)² −9 = 0.
4x = 0 soit x = 0 ; 4x-6=0 ; 4x = 6 ; x = 6 / 4 = 1,5.

.
.

Exercice 5.
Le dessin ci-dessous représente une figure composée d’un carré ABCD et d’un rectangle DEFG.
E est un point du segment [AD]. C est un point du segment [DG].
Dans cette figure la longueur AB peut varier mais on a toujours : AE = 15 cm et CG = 25 cm.

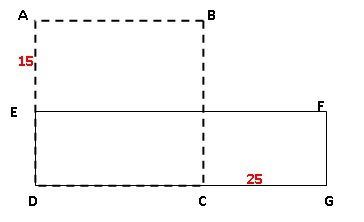
1. Dans cette question on suppose que : AB = 40 cm.
40 x 40 = 1600 cm².
a. Calculer l’aire du carré ABCD.
b. Calculer l’aire du rectangle DEFG.
ED = 40 -15 = 25 cm ; DG = 40 +25 = 65 cm ; aire du rectangle : 25 x 65 = 1625 cm².
2. Peut-on trouver la longueur AB de sorte que l’aire du carré ABCD soit égale à l’aire du rectangle DEFG?
Si oui, calculer AB. Si non, expliquer pourquoi.
Aire du carré de côté a : a².
Aire du rectangle : (a-15) (a+25) = a² +25a-15a-15 x25 = a² +10a-375.
Si les aires sont égales : a² = a² +10a-375.
10a = 375 ; a = 37,5 cm.

Exercice 6.
On considère un cône de révolution de hauteur 5 cm et dont la base a pour rayon 2 cm. Le point A est le sommet du cône et O le centre de sa base. B est le milieu de [AO].
1. Calculer le volume du cône en cm³. On arrondira à l’unité.
V = 1 /3 pr² h = 3,14 / 3 x2² x 5 =20,94 ~21 cm3.
2. On effectue la section du cône par le plan parallèle à la base qui passe par B. On obtient ainsi un petit cône. Est-il vrai que le volume
du petit cône obtenu est égal à la moitié du volume du cône initial ?
Faux, rayon et hauteur sont divisés par 2 ; le volume du petit cône est égal au 8^è du volume du grand cône.

Exercice 7.
Des élèves participent à une course à pied. Avant l’épreuve, un plan leur a été remis.
Il est représenté par la figure ci-dessous.
On convient que : • Les droites (AE) et (BD) se coupent en C.
• Les droites (AB) et (DE) sont parallèles.
• ABC est un triangle rectangle en A.

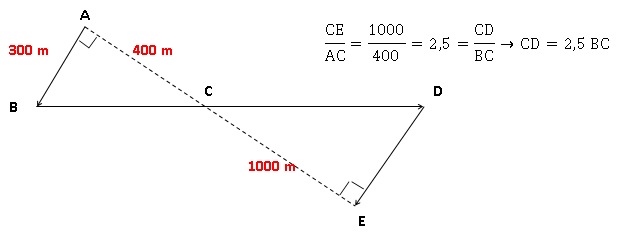
Calculer la longueur réelle du parcours ABCDE.
BC² = AB² +AC² = 300² +400² = 2500 ; BC = 500 m. CD = 2,5 x500 = 1250 m.
On passe des dimensions du triangle ANC à celles du triangle CDE en les multipliant par 2,5 : DE = 300 x2,5 = 750 m.
300 + 500 +1250 +750 = 2800 m.

Problème. Partie 1.
À partir du 2 Janvier 2012, une compagnie aérienne teste un nouveau vol entre Nantes et Toulouse.
Ce vol s’effectue chaque jour à bord d’un avion qui peut transporter au maximum 190 passagers.
1. L’avion décolle chaque matin à 9 h 35 de Nantes et atterrit à 10 h 30 à Toulouse.
Calculer la durée du vol.
10 h30 -9 h35 = 55 minutes.
2. Le tableau suivant donne le nombre de passagers qui ont emprunté ce vol pendant la première semaine de mise en service. L’information concernant
le mercredi a été perdue.

Jour
lundi
mardi
mercredi
jeudi
vendredi
samedi
dimanche
Total

Nombre de passagers
152
143

164
189
157
163
1113

a. Combien de passagers ont emprunté ce vol mercredi ?
1113 -152-143-164-189-157-163=145.
b. En moyenne, combien y avait-il de passagers par jour dans l’avion cette semaine là ?
1113 / 7 = 159.
3. À partir dumois de février, on décide d’étudier la fréquentation de ce vol pendant douze semaines. La compagnie utilise une feuille de calcul indiquant le nombre de passagers par jour.

=MOYENNE(J12:J13)

A
B
C
D
E
F
G
H
I
J

1

lundi
mardi
mercredi
jeudi
vendredi
samedi
dimanche
Total
Moyenne

2
semaine1
157
145
142
159
190
156
161
1110
159

3
semaine2
147
158
156
141
141
152
155
1050
150

4
semaine3
153
148
162
149
160
146
163
1081
154

5
semaine4
168
156
162
157
166
158
161
1128
161

6
semaine5
163
169
170
162
167
169
162
1162
166

7
semaine 6
156
167
171
173
165
165
162
1159
166

8
semaine 7
173
172
168
173
161
162
167
1176
168

9
semaine8
168
166
170
173
168
176
165
1186
169

10
semaine 9
176
175
175
171
172
178
173
1220
174

11
semaine 10
185
176
172
180
185
171
171
1240
177

12
semaine 11
178
181
183
172
178
172
173
1237
177

Moyenne sur trois mois
166

a. Quelle formule a-t-on saisie dans la cellule 12 pour obtenir le nombre total de passagers au cours de la semaine 1 ?
=SOMME(B2:H2)
b. Quelle formule a-t-on saisie dans la cellule J2 pour obtenir le nombre moyen de passagers par jours au cours de la semaine 1 ?
=MOYENNE(B2:H2)
4. Le nombre moyen de passagers par jour au cours de ces douze semaines est égal à 166. La compagnie s’était fixé comme objectif d’avoir un nombre
moyen de passagers supérieur aux 80% de la capacité maximale de l’avion. L’objectif est-il atteint ?
190 x0,80 = 152, valeur inférieure à 166. L'objectif est atteint.
Partie 2.
Quand l’avion n’est plus très loin de l’aéroport de Toulouse, le radar de la tour de contrôle émet un signal bref en direction de l’avion. Le signal atteint l’avion et revient
au radar 0,000 3 seconde après son émission.

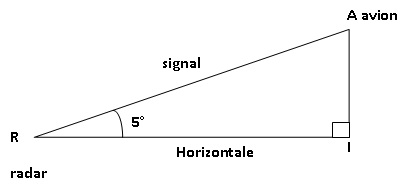
1. Sachant que le signal est émis à la vitesse de 300 000 kilomètres par seconde, vérifier qu’à cet instant, l’avion se trouve à 45 kilomètres du radar de la tour de contrôle.
aller + retour = 2AR = 300 000 x0,000 3 = 90 ; AR = 90 / 2 = 45 km.
2. La direction radar-avion fait un angle de 5°avec l’horizontale. Calculer alors l’altitude de l’avion à cet instant. On arrondira à la centaine de mètres près.
On négligera la hauteur de la tour de contrôle.
sin 5 = AI / AR ; AI = AR sin 5 = 45 x sin 5 =3,992 ~3,9 km.
Partie 3.
En phase d’atterrissage, à partir du moment où les roues touchent le sol, l’avion utilise ses freins jusqu’à l’arrêt complet. Le graphique ci-dessous représente la distance
parcourue par l’avion sur la piste (en mètres) en fonction du temps (en secondes) à partir du moment où les roues touchent le sol. En utilisant ce graphique, répondre aux questions suivantes :

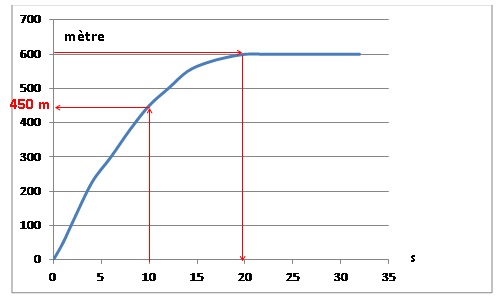
1. Quelle distance l’avion aura-t-il parcourue 10 s après avoir touché le sol ? 450 m.
2. Expliquer pourquoi au bout de 22 s et au bout de 26 s la distance parcourue depuis le début de l’atterrissage est la même.
Le graphique est une droite horizontale : l'avion est à l'arrêt.
3. À partir du moment où les roues touchent le sol, combien de temps met l’avion pour s’arrêter ? 20 s.

menu