Mathématiques, Brevet des collèges Métropole 09 / 2012

Mathématiques, Brevet des collèges Métropole 09 / 2012

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
1. 2.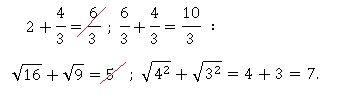
3. Le PGCD de 52 et 39 est 13. Vrai.
52 = 13 x4.
4. Pour b = 0,5, 4b² +1 = 2. Vrai.
4 x0,5² +1 = 4 x0,25 +1 = 2.
5. Pour toute valeur de b, 4b² +1 = 2. Faux.
Pour b = 0, 4b² +1 =1.

.
.

Exercice 2.
Un cybercafé est ouvert depuis une semaine. Dans ce cybercafé, on peut choisir entre deux moteurs de recherche : Youpi et Hourra. Le tableau ci-dessous donne les moteurs de recherche utilisés par les 992 premiers utilisateurs lors de la semaine d’ouverture.
Moteur Youpi : 789 utilisateurs ; Moteur Hourra : 203 utilisateurs.
La probabilité pour qu’un utilisateur pris au hasard dans ce cybercafé choisisse le moteur Youpi est-elle proche de 0,4 ; de 0,6 ou de 0,8 ?
789 / 992 =0,795, proche de 0,8.

Exercice 3.
La copie d’écran ci-dessous montre le travail qu’a effectué Camille à l’aide d’un tableur à propos des fonctions g et h définies par :
g (x)= 5x² +x −7 et h(x) = 2x −7.
Elle a recopié vers la droite les formules qu’elle avait saisies dans les cellules B2 et B3.

B2
=5*B1*B1+B1-7

A
B
C
D
E
F

1
x
-2
-1
0
1
2

2
g(x) =5x²+x-7
11
-3
-7
-1
15

3
h(x)=2x-7
-11
-9
-7
-5
-3

1. Donner un nombre qui a pour image −1 par la fonction g .
-1 = 2x-7 ; -1 +7 = 2x ; 6 = 2x ; x = 6 / 2 ; x =3.
2. Écrire les calculs montrant que : g (−2) = 11.
3. Quelle formule Camille a-t-elle saisie dans la cellule B3 ?
=2*B1-7
4. a. Déduire du tableau une solution de l’équation 5x² +x −7 = 2x −7.
x=0.
b. Cette équation a-t-elle une autre solution que celle trouvée grâce au tableur ?
5x² +x -2x= 7 −7=0
x(5x-1)=0 ; x = 0 et 5x-1 = 0 soit x = 1 / 5.

Exercice 4.
Dans la figure ci-contre, qui n’est pas à l’échelle, on sait que :
(BC) // (DE)
B, A et E sont alignés
C, A et D sont alignés.
Démontrer que la longueur du segment [BC] est 4,9 cm.

.
.

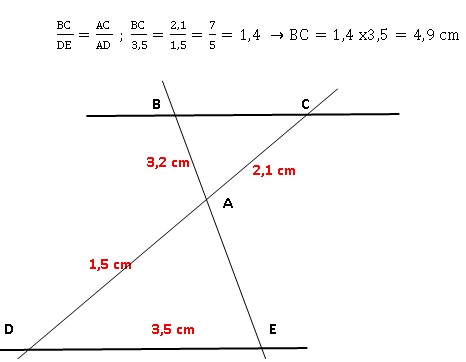
Exercice 5.
JGIH est un parallélogramme,

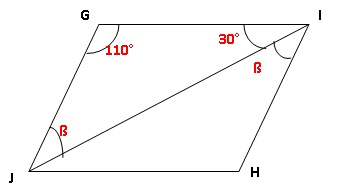
Calculer lamesure de l’angle ß.
Dans le triangle IJG : ß +110 +30 = 180 ; ß = 40°.

Exercice 6.
On veut réaliser un tipi qui aura la forme d’une pyramide ayant
pour base un rectangle ABCD de centre H et pour hauteur [SH]
Le tipi aura les dimensions suivantes :
AD = 1,60 m, CD = 1,20 m et SH = 2,40 m.

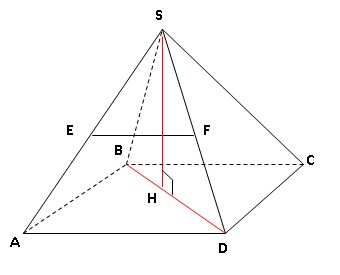
1. Calculer le volume V de cette pyramide, en m³.
On rappelle que V = 1 / 3 xB ×h où h désigne la hauteur et B l’aire de la base.
V = 1 / 3 xAD xCD xSH = 1 / 3 x1,6 x1,2 x2,4 = 1,536 m³.
2. Calculer la longueur BD.
BD² = AB²+AD² = 1,2²+1,6² = 4 ; BD = 2 m.
3. L’armature du tipi, constituée du cadre rectangulaire ABCD et des quatre arêtes latérales issues de S, est faite de baguettes de bambou.
Dans cette question on n’attend pas de démonstration rédigée.Citer une propriété et présenter clairement un calcul suffit.
a. Montrer que : SD = 2,60 m.
Triangle rectangle SHD : SD² = SH²+HD² = 2,4²+1² = 6,76 ; SD = 2,6 m.
b. On ajoute à l’armature une baguette [EF] comme indiqué sur le dessin de sorte que (EF) // (AD) et SF = 1,95 m. Calculer EF.
AD / EF = SD / SF = 2,6 / 1,95 = 4 / 3 ~1,33 ;
EF = 3 AD / 4 = 3 x1,6 / 4 = 1,2 m.
4. On a trouvé dans un magasin des tiges de bambou de 3 m. Une tige peut être coupée pour obtenir deux baguettes mais une baguette ne peut être fabriquée par collage de deux morceaux de bambou.
Combien faut-il acheter de tiges de bambou, au minimum, pour réaliser les neuf baguettes de l’armature du tipi ?
Pour la base, 2 tiges de banbou coupées suffisent. ( AB +AD < 3 m).
4 tiges de banbou pour les 4 arêtes.
Une tige de banbou coupée pour EF.
Total : 7 tiges.

Exercice 7.
Rémi s’est inscrit à son premier triathlon « distance olympique ».
Il devra effectuer : 1,5 km de natation, puis 40 km de cyclisme, puis 10 km de course à pied.
Il a reçu les informations suivantes. Les deux schémas ne sont pas à l’échelle.

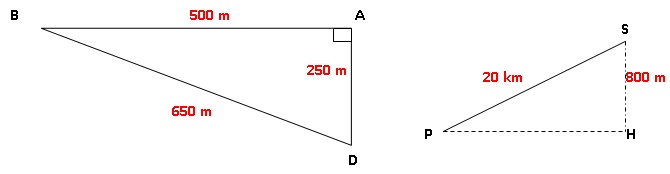
Natation : Partir du point D, rejoindre la bouée A à 250 m du départ, la contourner à 90° sur la gauche, aller jusqu’à la bouée B, la contourner encore à
gauche et rejoindre le point de départ D qui est à 650 m de la bouée B.
Cyclisme : Départ au point P au pied du col, montée régulière de 20 km jusqu’au sommet S du col avec un dénivelé de 800 m, puis descente par
la même route et retour au point P.
Course à pied : 5 km à parcourir deux fois.
Préparation du triathlon.
1. Partie natation
Rémi prévoit de parcourir 1 km toutes les 20 minutes. Expliquer pourquoi, s’il nage régulièrement, il devrait mettre 28 minutes pour la partie natation.
Distance : 500 +250 +650 = 1400 m = 1,4 km.
Durée : 1,4 x 20 = 28 minutes.
2. Partie cyclisme
a. Vérifier par un calcul que la valeur arrondie au mètre près de PH est 19 984 mètres.
PH²=PS²-SH² = 20²-0,8² = 400-0,64=399,36 ; PH = 19,984 km.
b. Rémi sait qu’avec une telle pente il peut prévoir 1 h 30 min pour cette partie du triathlon.
Calculer la pente moyenne du col que doit escalader Rémi.
Pente = SH / PH = 0,8 / 19,984 ~0,04 ( 4 %).
3. Partie course à pied
Pour la dernière partie de son triathlon, Rémi prévoit de mettre 20 minutes pour chacun des deux tours du circuit de 5 km.
Déterminer en km/h sa vitesse moyenne pour la course à pied s’il respecte ses prévisions.
10 km parcourus en 40 minutes soit 2 / 3 heure.
Vitesse = distance / durée = 10 / (2 /3) = 10 x3 / 2 = 15 km /h.
4. Totalité du triathlon
Remplir le tableau récapitulatif :

Epreuves
Natation
Cyclisme
Course à pied
Total

temps prévus
28 min
1 h 30 min
40 min
2 h 38 min.

Après le triathlon
Pendant la course, Rémi portait à la cheville une puce électronique qui a enregistré ses différents temps de passage.
Le soir même il a reçu par internet ses résultats. Ceux-ci sont présentés sous la forme d’un graphique où figurent trois points R₁ (fin de la natation),
R₂ (fin du cyclisme) et R₃ (fin du triathlon) qui décomposent son parcours en trois parties.
1. Marquer sur le graphique les trois points correspondant à ce qu’il avait prévu de réaliser.

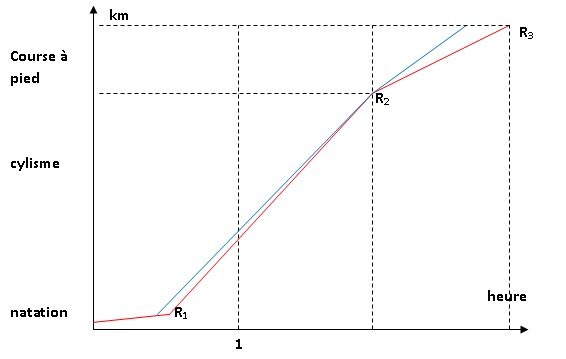
2. Dans cette question aucune justification n’est attendue.
a. Rémi a-t-il respecté ses prévisions au niveau du temps total ? Non.
b. Sur quelle(s) partie(s) du parcours a-t-il fait mieux que prévu ?
Sur aucune parties du parcours.
3. Au cours du deuxième tour à pied Rémi a failli abandonner et il a fini son triathlon très affaibli, déshydraté par la chaleur. Alors qu’il pesait 75 kg avant la course il ne pesait plus que 71 kg à l’arrivée. Rémi était-il proche du malaise à la fin de son triathlon ?
Perte de poids en pourcentage : (75-71 / 75 x100 ~ 5,3 %, valeur supérieure à 4 %, risque de malaise.

menu