Mathématiques,
Brevet des collèges Polynésie 09 / 2012
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
On donne le programme de calcul suivant :
• Choisir un nombre.
• Lui ajouter 1.
• Calculer le carré de cette somme.
• Enlever 16 au résultat obtenu.
1. a. Vérifier que,
lorsque le nombre de départ est 4, on obtient comme résultat 9.
4+1 =5 ; 52=25 ; 25-16 = 9.
b. Lorsque le
nombre de départ est (−3). quel résultat obtient-on ?
-3 +1 = -2 ; (-2)2 = 4 ; 4-16 = -12.
c. Le nombre de
départ étant x, exprimer le résultat final en fonction de x,
On appelle P cette expression.
P=(x+1)2-16.
d. Vérifier que P =
x2 +2x −15.
P = x2 +2x+1-16 = x2+2x-15.
2. a. Vérifier que
(x −3)(x +5) = P.
Différennce de deux carrés : P = (x+1)2-42=(x+1-4)(x+1+4)
=(x-3)(x+5).
b. Quels nombres
peut-on choisir au départ pour que le résultat final soit 0 ?
Justifier votre réponse.
Pour qu'un produit de facteurs soit nul il faut et il suffit que l''un
des facteurs soit nul.
x-3 = 0 ; x = 3 ; x+5 = 0 ; x = -5.
Exercice
2. QCM.
1. L’écriture sous
forme scientifique de 102 ×21×10−7 est :
21 x10-7+2=21 x10-5 = 2,1 10-4.
Réponse C.
2. Le premier
quartile Q1 de la série de valeurs : 58 ; 55 ; 61 ; 70 ; 61
; 65 ; 58 ; 55 ; 72 est :
Classer les valeurs par ordre croissant : 55 ; 55 ; 58 ; 58 ; 61 ; 61 ;
65 ; 70 ; 72.
Le premier quartille est 58. Réponse B.
3. Racine carrée
(500) = racine carrée (100 x5) = racine carrée (102) x
racine carrée (5) = 10 x racine carrée (5). Réponse A.
4. Les solutions de
l’inéquation −2x + 5 >
7 sont les nombres x tels que :
-2x > 7-5 ; -2x >2 ; -x >1 ; x < -1. réponse D.
Exercice 3.
Une usine deMoorea fabrique du jus de fruits.
Soit C une fonction qui, à une quantité de jus fabriquée en litre(s)
associe le coût de fabrication en F. On a représenté ci-dessous la
fonction C pour une quantité de jus comprise entre 0 et 130 litres.
À l’aide du
graphique ci-dessus, répondre aux questions suivantes :
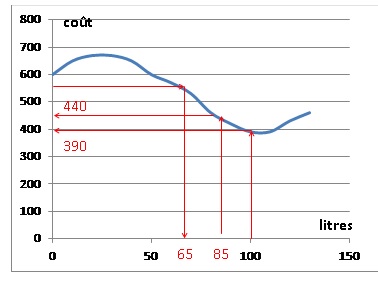
1. a. Donner le
coût de fabrication de 100 litres de jus. 390 F.
b. Pour quelle(s)
quantité(s) de jus, le coût de fabrication est-il supérieur à 550 F ? Moins de 65 L.
2. a. Donner
l’image de 85 par la fonction C. 440 F.
b. Lire C(75). 560 F.
c. Donner le(s)
antécédent(s) de 600 par La fonction C. 0 et 54.
|
|
|
Exercice 4.
Un
sculpteur fabrique un « umete » en bois (récipient) ayant la forme
d’une demi-sphère de rayon 15 cm (l’épaisseur du umete est supposée
négligeable).
1. Vérifier que la
valeur exacte du volume du umete est égale à 2 250 p cm3.
Volume d'une demi-sphère : V =2 / 3 p r3 = 2 / 3 x153
p = 2 250 p cm3.
2.
Dans cette question, toute trace de recherche, même incomplète, sera
prise en compte dans l’évaluation. Pourra-t-on verser dans ce umete 7
litres de lait de coco sans déborder ? Justifier.
V = 2250 x3,14 = 7065 cm3 = 7,065 L, valeur supérieur à 7 L.
On pourra verser 7 L de lait de coco.
Exercice
5.
Dans tout cet exercice,
les figures ne sont pas à l’échelle.
Moana décide de participer à un triathlon. Il prend connaissance des
parcours des trois épreuves : natation, cyclisme et course à pied.
1. 1re épreuve : la
natation
Le départ se fait sur la plage au point D, Les triathlètes doivent
contourner une bouée située au point B, puis rejoindre la plage au
point A. On donne AB = 800 m et AD = 2 341 me t (AB) ⊥ (BD).
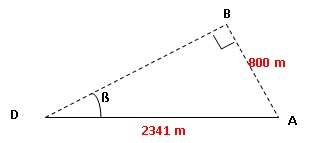
a. Calculer la
longueur du parcours « natation » représenté par DB + BA.
Donner la réponse arrondie au mètre.
DB2 = AD2-AB2 = 23412-8002=4
840 281 ; DB ~2200 m .
2200 + 800 = 3000 m.
b. Calculer sin� ß;
en déduire la mesure de l’angle �ß arrondie au degré.
sin ß = AB / AD = 800 / 2341 =0,342
; ß = 19,98 ~ 20°.
|
|
|
|
2e
épreuve :
Le circuit « vélo » est un arc de cercle de centre O. Le départ a lieu
au point M et l’arrivée au point N.
Un spectateur situé en O voit le premier tronçon ÙMC parcouru par le
cycliste sous un angle de 81,5 °.
On souhaite déterminer la mesure de l’angle ƒß.
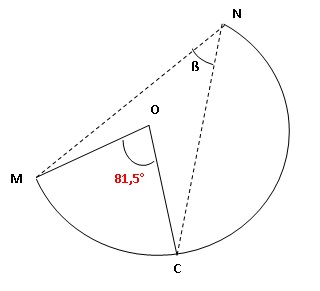
a. Dans cet
exercice, pour déterminer la mesure de l’angle ß, laquelle des quatre
propriétés suivantes faut-il utiliser ?
• Si deux angles inscrits dans un cercle interceptent le même arc,
alors ils ont la même mesure,
• Si un triangle est inscrit dans un cercle et a pour côté un diamètre
de ce cercle, alors c’est un triangle rectangle.
• Dans un cercle, si un angle inscrit
et un angle au centre interceptent le même arc, alors la mesure de
l’angle inscrit est la moitié de la mesure de l’angle au centre,
• Dans un triangle isocèle, les angles à la base ont la même mesure.
b. Donner alors la
mesure de l’angleƒ ß.
81,5 /2 = 40,75 °.
3e épreuve : la
course à pied
Le circuit « course à pied ») est un aller-retour de 20 km (10 km à
l’aller et 10 km au retour).
Pour le trajet aller, qui s’effectue dans le sens du vent, Moana estime
que sa vitesse moyenne sera de 16 km/h.
Pour le trajet retour,à cause du vent de face et de la fatigue Moana
pense courir à la vitesse moyenne de 10 km/h.
Peut-on affirmer que sa vitesse moyenne sera de 13 km/h sur l’ensemble
du circuit « course à pied » ? Justifier votre réponse.
Distance 20 km. Durée du trajet aller : 10 / 16 = 5 / 8 = 0,625 h.
Durée du trajet retour : 10 / 10 = 1 h. Durée totale : 1,625 h.
Vitesse moyenne de la course à pied : 20 / 1,625 ~12,3 km /h, valeur différennte de 13
km /h.
Exercice 6.
Un bijoutier achète un lot de 220 perles de Tahiti.
Un contrôleur qualité s’intéresse à leurs formes (ronde ou baroque) et
à leurs couleurs (grise ou verte).
• 35% des perles sont de couleur verte, et parmi celles ci 13 sont de
forme ronde.
• Il y a 176 perles de forme baroque,
Il note les résultats dans la feuille de calcul ci-dessous
|
A
|
B
|
C
|
D
|
1
|
|
Rondes
|
Baroques
|
Total
|
2
|
Grises
|
143-112=31
|
176-64=112
|
220-77=143
|
3
|
Vertes
|
13
|
64
|
220
x0,35 =77
|
4
|
Total
|
220-176=44
|
176
|
220
|
A. 1. Pour obtenir
le nombre de perles vertes à partir des informations données dans
l’énoncé, quelle formule doit-il saisir en D3 ? Parmi les quatre
formules proposées :
=D4*1,35 ; 220*35 / 100 ; =D4 * 0,35
; =B3 + C3
2. Compléter le
tableau ci-dessus.
3. On choisit au
hasard une perle de ce lot.
a. Quelle est la
probabilité pour que cette perle soit de forme baroque ? 176 / 220 = 0,80.
b. Quelle est la
probabilité de tirer une perle baroque verte ? 64 / 220 ~0,29.
B. Ce bijoutier se
fournit chez un perliculteur de l’archipel des Gambier.
L’acheminement vers Tahiti des lots de perles, s’effectue selon deux
tarifs :
• Tarif «Ho’ » : 2 300 F par lot.
• Tarif « Piti » : 7 000 F fixe et 900 F par lot
1. Calculer, pour
chaque tarif, le montant de l’acheminement de 4 lots.
Tarif "Ho" : 2300 x4 = 9200 F.
Tarif "Piti" : 7000 + 4 x900 = 10600 F.
2. On note x le
nombre de lots de perles expédié(s).
a. Exprimer, en
fonction de x, le montant de l’acheminement avec le tarif Ho’. 2300 x.
b. Exprimer, en
fonction de x, le montant de l’acheminement avec le tarif Piti. 7000 +900x.
|
|
3. a.
Soit f et g les deux fonctions définies par :
f (x)=2300x et g (x)=900x +7000.
Dans le repère ci-dessous, construire les représentations graphiques
des fonctions f et g .
b. Par lecture
graphique, déterminer à partir de combien de lots expédiés, le tarif
Piti est plus avantageux pour le bijoutier que le tarif Ho’e.
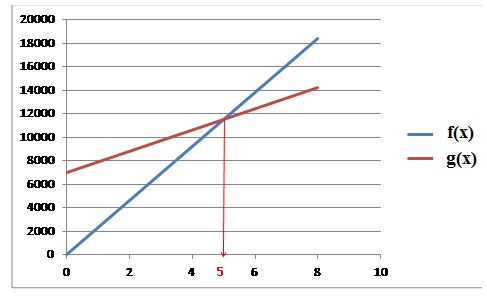
Pour x >5, le tarif Piti est le plus intéressant.
|
|