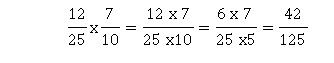
Mathématiques, Brevet des collèges Nlle Calédonie 2012 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Exercice 1.  QCM   1. 2.  Une mouette parcourt 4,2 kilomètres en 8 minutes. Quelle distance aurait-elle parcourue en une heure, si elle gardait la même vitesse ? 4,2 / 8 x60 =31,5 km / h. 3. Quelle est la notation scientifique de (4×10−3)2 ? 16 x10-6 = 1,6 10-5. 4. Un bidon contient 25 L. Si j’augmente de 2% sa contenance, alors j’obtiens : 25 x1,02=25,5 L. 5. Donner la valeur médiane de la série statistique suivante : 1 ; 2 ; 2,4 ; 3 ; 3,5 ; 3,7 ; 3,8 ; 4 ; 4,2 ; 4,2 ; 7. . . Exercice 2. Un concours de pêche est organisé avec 8 bateaux participants. Les organisateurs souhaitent former au hasard 4 équipes de 2 bateaux. Pour cela, un tirage au sort est organisé. Dans une urne se trouvent 8 fanions indiscernables au toucher : 2 rouges, 2 oranges, 2 violets et 2 verts. Les bateaux ayant un fanion de même couleur seront dans la même équipe. 1. Quelle est la probabilité de sortir un fanion rouge au premier tirage ? 2 cas favorables sur 8 cas possibles ; la probabilité de tirer un fanion rouge est 2 / 8 = 0,25. 2. Aux deux premiers tirages, un fanion vert et un fanion orange ont été sortis. a. Quels fanions se trouvent encore dans l’urne avant le troisième tirage ? 2 rouge, 1 orange, 2 violet et 1 vert. b. Combien y a-t-il de fanions dans l’urne avant le troisième tirage ? 6. c. Calculer la probabilité de l’évènement A : « un fanion d’une autre couleur que le vert ou le orange est tiré ». 4 cas favorables sur 6 possibles ; la probabilité est égale = 4 / 6 = 2 /3 ~0,67. Exercice 3. Une société propose des sorties en mer sur un voilier. Il n’y a qu’un seul tarif adulte et qu’un seul tarif enfant. Un premier groupe composé de 4 adultes et 6 enfants a payé au total 52 800 F. Un deuxième groupe composé de 6 adultes et 4 enfants a payé au total 63 200 F pour la même sortie. 1. Un groupe, composé de 10 adultes et 10 enfants, a un budget total de 120 000 F. Ils se demandent s’ils auront assez d’argent pour une sortie en voilier. Sans connaître le prix des places, Émilie a une astuce pour répondre à cette question. Donner sa réponse et expliquer son raisonnement. Le premier groupe ( 4 adultes + 6 enfants) paie : 52 800 F. Le second groupe ( 6 adultes + 4 enfants) paie : 63 200 F. Additionner ( 10 adultes + 10 enfants paient : 25800 +63200=116000 F,  inférieur à 120000 F Ils auront assez s'argent. 2. Le petit frère d’Émilie affirme qu’une place adulte coûte 7 000 F et qu’une place enfant coûte 2 500 F. A-t-il raison? Justifier. 7000 x4 +2500 x6=28000 + 15000 =43000, différent de 52800 ; il a tord. 3. Pour cette sortie, combien payera un adulte accompagné d’un enfant ? a : prix de la sortie adulte ; b : prix de la sortie enfant. 4a+6b=52800 ; 2a +3b = 26400 soit a = 13200 -1,5 b. 6a+4b=63200 ; 3a+2b=31600. 3(13200-1,5b)+2b = 31600 ; 39600-2,5b =31600 ; 2,5 b=8000 ; b=8000 / 2,5 =3200 F. a=13200-1,5 x3200 =8400 F. Prix pour un adulte et un enfant : 8400+3200 = 11600 F. On aurait aussi pu faire : 116000 / 10. Exercice 4. Le niveau de la mer monte et descend suivant le cycle des marées. Les deux schémas ci-dessous représentent lamême plage parfaitement lisse, à deux instants de la journée. 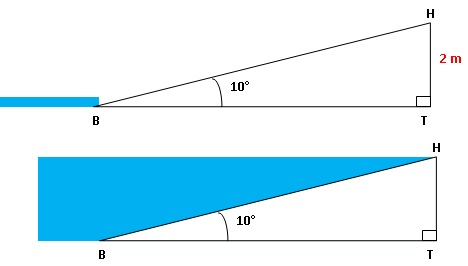1. Calculer la longueur BH, en mètres, de plage recouverte par la mer à marée haute. Donner l’arrondi au dixième près. sin 10=HT / BH= 2 / BH ; BH = 2 / sin 10 ~11,5 m. 2. Sur une autre plage de pente différente (mais toujours parfaitement lisse), la mer a recouvert la plage jusqu’au point L. Deux heures plus tard, la mer s’est retirée et se situe désormais au point A. Sur le schéma, les points S, B et E sont alignés. Ils correspondent au niveau horizontal. Démontrer que les droites (AB) et (LE) sont parallèles. Calculer la longueur AB, en mètres, du niveau vertical actuel de la mer. 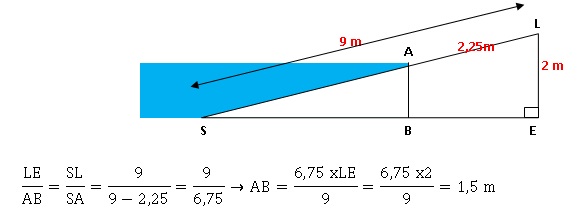Les droites (AB) et (LE), perpendiculaires à (SE), sont parallèles. Exercice 5. La figure ci-dessous est un hexagone régulier ABCDEF inscrit dans un cercle C. Cette figure n’est pas en vraie grandeur. 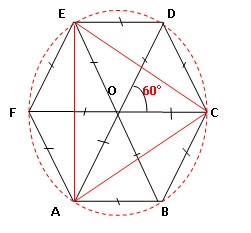1. Construire un hexagone régulier, inscrit dans un cercle de rayon 3 cm. 2. Calculer la mesure de l’angle� COE. 2 x60 = 120°. 3. Montrer que l’angle �CAE mesure 60 °. L'angle inscrit CAE intercepte le même arc que l'angle au centre COE. Sa mesure est égale à la moitié de celle de l'angle COE, soit 60°. 4. Quelle est la nature du triangle CAE ? Justifier. L'angle inscrit CEA intercepte le même arc que l'angle au centre COA. Sa mesure est égale à la moitié de celle de l'angle COA, soit 60°. L'angle inscrit ECA intercepte le même arc que l'angle au centre EOA. Sa mesure est égale à la moitié de celle de l'angle EOA, soit 60°. Le triangle AEC est équilatéral. . . Pour attirer davantage de visiteurs dans sa ville, un maire décide de faire construire l’Aquarium du Pacifique. Les architectes prévoient de poser un énorme aquarium à l’entrée, dont la vitre a une forme sphérique. Partie 1. La figure ci-dessous représente la situation. Cette figure n’est pas en vraie grandeur. 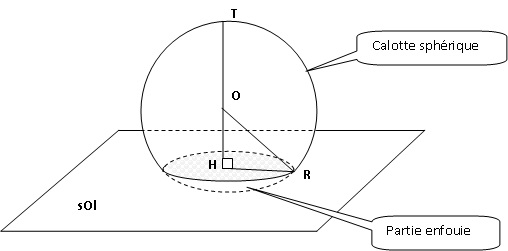Calculer le volume en m3 d’une boule de rayon 5 m. Donner l’arrondi à l’unité près. V = 4 / 3 pr3 = 4 / 3 x3,14 x53 ~ 524 m3. 2. En réalité, l’aquarium est implanté dans le sol. La partie supérieure (visible aux visiteurs) est une « calotte sphérique». La partie inférieure (enfouie) abrite les machines. a. Quelle est la nature géométrique de la section entre le plan horizontal du sol et l’aquarium (la partie grisée sur la figure) ? Un disque. b. Le point O désigne le centre de la sphère. On donne les dimensions réelles suivantes : OH = 3 m ; RO = 5 m ; HR = 4 m, où H et R sont les points placés sur le sol comme sur la figure. Le triangle OHR est-il rectangle ? Justifier. OR2 = 52 = 25. OH2+HR2 = 32 +42 = 9+16 =25. OR2 =OH2+HR2 : d'après la réciproque du théorème de Pythagore, le triangle OHR est rectangle en H. 3. a. T est un point de la sphère tel que les points T, O, H soient alignés comme sur la figure. Calculer la hauteur HT de la partie visible de l’aquarium. TH = OT +OH = 5 +3 = 8 m. b. Le volume d’une calotte sphérique de rayon 5 m est donné par la formule : Vcalotte =p×h2 /3 ×(15−h) où h désigne sa hauteur (correspondant à la longueur HT sur la figure). Calculer le volume en litres de cette calotte sphérique. Vcalotte =3,14 x82 /3 x(15-8)~469,144 m3 ou 469 144 L. c. Pour cette question, on prendra comme volume de l’aquarium 469 000 litres. Des pompes délivrent à débit constant de l’eau de mer pour remplir l’aquarium vide. En 2 heures de fonctionnement, les pompes réunies y injectent 14 000 litres d’eau de mer. Au bout de combien d’heures de fonctionnement, les pompes auront-elles rempli l’aquarium? 469000 / 7000 ~67 heures. Partie 2. Voici un extrait d’article trouvé dans une revue scientifique : « Si l’Homme ne change pas son comportement de pollueur, il n’y aura plus aucun poisson à l’état sauvage dans les océans. 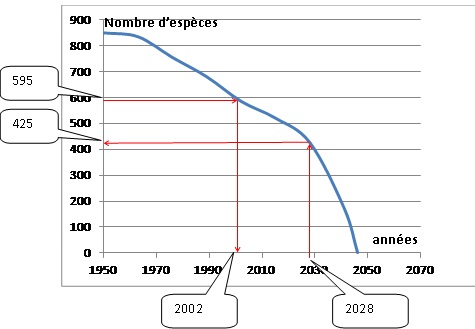» Le graphique ci-dessus donne la courbe représentative d’une fonction f qui prévoit l’évolution des espèces restantes de poissons trouvées en mer. 1. D’après le graphique : a. Déterminer le nombre d’espèces restantes de poissons en 2028. 425. b. En quelle année restait-il 595 espèces de poissons ? 2002. Donner une estimation de l’année de disparition prévue de toutes les espèces de poissons de pêche. 2046. 2. La biologiste de l’Aquarium du Pacifique aménage une salle dédiée à trois espèces de petits poissons notées A, B et C. Voici le tableau donnant le nombre de poissons de chaque espèce dont elle dispose : Espèce de petits poissons A : 154 ; B : 105 ; C : 126. a. Calculer le PGCD des nombres 154 et 105, par l’algorithme de votre choix et en détaillant les étapes. Algorithme d'Euclide : 154 = 105 +49 ; 105 = 2 x49 +7 ; 49 = 7 x7. PgCd(154 ; 105) = 7. b. Combien faudrait-il de bassins au minimum pour qu’ils contiennent exactement le même nombre de poissons de chacune des espèces A, B et C ? 126 = 7 x18 et 18, 15 et 22 n'ont pas de diviseur commun autre que 1. Le PGCD de 154, 105 et 126 est dionc 7. c. Donner pour chaque espèce, le nombre de poissons qu’il y aurait alors dans un bassin. 7 bassins contenant 154 / 7 = 22 poissons A, 105 / 7 =15 poissons B et 126/ 7 = 18 poissons C.

menu