Mathématiques,
Brevet des collèges Centres étrangers 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice 1. QCM.
1. Les solutions de
l’équation (x + 7)(2x − 7) = 0 sont :
-7 et 3,5 vrai
; 7 et -3,5 ; -7 et 5.
x+7 = 0 soit x = -7 ; et 2x-7=0 soit x =
3,5.
2. La (ou les) solution (s) de
l’inéquation −2(x +7) <= −16 est (sont) :
tous les nombres inférieurs ou égaux à 1 ; tous les nombres supérieurs ou égaux à 1 vrai ; 1.
2(x +7) >= 16 ; x+7 >= 8 ; x >= 1.
3. La
forme développée de (7x −5)2 est.:
49x2-25 ; 49x2-70x+25 vrai ; 49x2-70x-25.
4. La forme factorisée de 9−64x2
est :
55x2 ; (3-8x)2 ; (3-8x)(3+8x) vrai.
5. Le liquide
rempli-il la moitié du verre ?
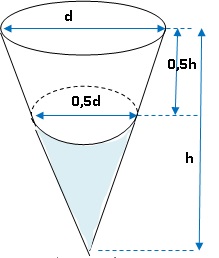
Volume du grand cône : 1 /3 *3,14 x(d / 2)2
x h ~ 0,26 d2h cm3.
Volume du petit cône : 1 /3 *3,14 x(d / 4)2
x h =
0,065 d2h cm3.
Volume du liquide : 0,065 d2h
cm3, moins de la moitié du verre.
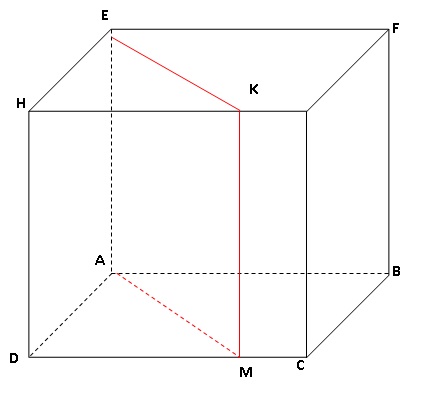
6. La section KMEA
du cube ABCDEFGH par un plan parallèle à une de ses arêtes est .
un parallélogramme non rectangle ; un carré ; un rectangle. Vrai.
Exercice 2.
On
considère l’expérience aléatoire suivante : on tire au hasard une carte
dans un jeu bien mélangé de 32 cartes (il y a 4 « familles » coeur,
trèfle, carreau et pique et on a 8 coeurs, 8 trèfles, 8 carreaux et 8
piques).
On relève pour la carte tirée la « famille » (trèfle, carreau, coeur ou
pique) puis on remet la carte dans le jeu et on mélange.
On note A l’évènement : « la carte tirée est un trèfle ».
1. Quelle est la
probabilité de l’évènement A ?
8 cas favorables sur 32 cas possibles soit 8 / 32 = 1,4 = 0,25.
2. On répète 24
fois l’expérience aléatoire ci-dessus. La représentation graphique
ci-dessous donne la répartition des couleurs obtenues lors des
vingt-quatre premiers tirages :
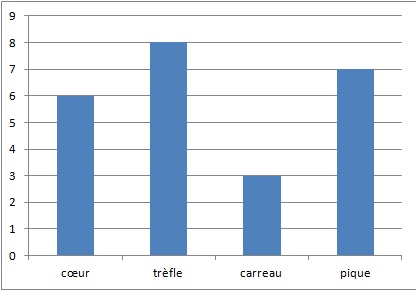
Calculer la fréquence d’une carte de la «
famille » coeur et d’une carte de la « famille » trèfle.
Famille coeur : 6 /24 = 0,25 ; famille trèfle 8 / 24 = 1 /3.
3. On reproduit la
même expérience qu’à la question 2. Arthur mise sur une carte de la «
famille » coeur et Julie mise sur d’une carte de la « famille » trèfle.
Est-ce que l’un d’entre deux a plus de chance que l’autre de gagner ?
Non, la probabilité de tirer un coeur est égale à celle de tirer un
trèfle.
|
| ... |
|
|
Exercice 3.
On considère un triangle ABC isocèle en A tel que
l’angle BAC mesure 50° et AB est égal à
5 cm. On note O le centre du cercle circonscrit au triangle ABC. La
droite (OA) coupe ce cercle,
noté (C), en un autre point M.
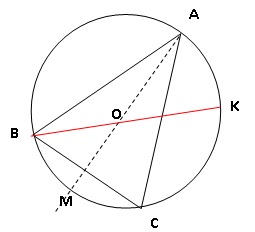
1. Quelle est la
mesure de l’angle BAM ? Aucune justification n’est demandée.
AM est à la fois médiane, médiatrice de BC et bissectrice de l'angleBAC
: 50 /2 =25°.
2. Quelle est la
nature du triangle BAM ? Justifier.
Le triangle BAM inscrit dans un demi cercle de diamètre AM est
rectangle en M.
3. Calculer la
longueur AM et en donner un arrondi au dixième de centimètre près.
Dans le triangle BAM, cos 25 = AB / AM ; AM = AB / cos 25 = 5 /cos 25 =
5,5 cm.
4. La droite (BO)
coupe le cercle (C) en un autre point K. Quelle est la mesure de
l’angle BKC?
Justifier.
Les angles inscrits BKC et BAC interceptent le même arc de cercle
BC.Ces angles ont la même mesure, 50°.
Exercice 4.
Le nombre d’abonnés à une revue dépend du prix de la revue.
Pour un prix x compris entre 0 et 20 €, le nombre d’abonnés est donné
par la fonction A telle que : A(x) = −50x +1250.
La recette, c’est-à-dire le montant perçu par l’éditeur de cette revue,
est donnée par la fonction R telle que : R(x) = −50x2 +1250x.
1. Le nombre
d’abonnés est-il proportionnel au prix de la revue ? Justifier.
Non, le graphe de la fonction A(x) n'est pas une droite passant
par l'origine.
2. Vérifier, par le
calcul, que A(10) = 750 et interpréter concrètement ce résultat.
A(10) = -50 x10 +1250 = 750.
750 abonnés payent la revue 10 €.
3. La fonction R
est-elle affine ? Justifier.
Non, le graphe de la fonction R(x)
n'est pas une droite.
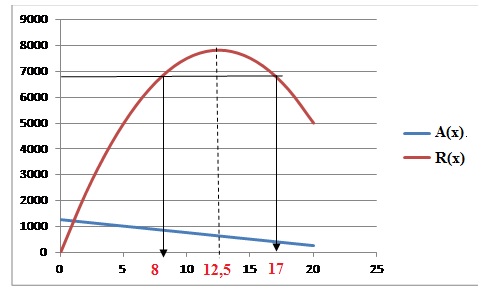
4. Déterminer graphiquement pour
quel prix la recette de l’éditeur est maximale.12,5 €
5. Déterminer
graphiquement les antécédents de 6 800 par R. 8 et 17.
6. Lorsque la revue
coûte 5 euros, déterminer le nombre d’abonnés et la recette.
A(5) = -50 x5 +1250 = 1000 abonnés.
R(5) = -50 x52 +1250 x5 = 5000 €.
|
|
|
|
Exercice 5. On considère la série
statistique donnant le SMIC
Année
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
SMIC
|
6,67
|
6,83
|
7,19
|
7,61
|
8,03
|
8,27
|
8,44
|
8,63
|
8,82
|
9,00
|
9,40
|
SMIC : salaire minimum interprofessionnel de croissance horaire brut en
euros de 2001 à 2011 (source : INSEE)
1. Quelle est l’étendue de cette
série ? Interpréter ce résultat.
Plus grande valeur - plus petite valeur = 9,40 -6,67 = 2,73.
2. Quelle est la
médiane ?
11 valeurs rangées par ordre croissant, la médiane est la 6è
soit 8,27.
3. Paul remarque
qu’entre 2001 et 2002, l’augmentation du SMIC horaire brut est de 16
centimes alors qu’entre 2007 et
2008, elle est de 19 centimes. Il affirme que « le pourcentage
d’augmentation entre 2007 et 2008 est supérieur à celui pratiqué entre
2001 et 2002 ». A-t-il raison ?
Pourcentage d'augmentation entre 2001 et 2002 : (6,83-6,67) /
6,67 x100 ~2,4 %.
Pourcentage
d'augmentation entre 2007 et 2008 : (8,63-8,44) / 8,44 x100 ~2,25
%. Il a tord.
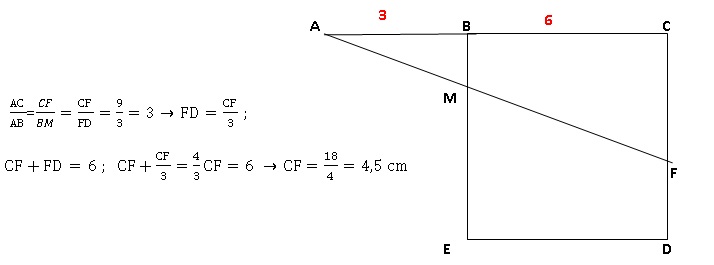
Exercice 6.
BCDE est un carré de 6 cm de côté. Les points A, B
et C sont alignés et AB = 3 cm.
F est un point du segment [CD]. La droite (AF) coupe le segment [BE] en
M.
Déterminer la longueur CF par calcul ou par construction pour que les
longueurs BM et FD soient égales.
|
|
Exercice 7.
On
peut lire au sujet d’un médicament :
« Chez les enfants (12 mois à 17 ans), la posologie doit être établie
en fonction de la surface corporelle du patient [voir formule
deMosteller]. »
« Une dose de charge unique de 70 mg par mètre carré (sans dépasser 70
mg par jour) devra être administrée »
Pour calculer la surface corporelle en m2 on utilise la
formule suivante :
Formule de Mosteller : Surface corporelle en m2 =racine
carrée [taille (en cm)×masse (en kg) / 3600 ]
On considère les informations ci-dessous :
Patient
|
Age
|
Taille
(m)
|
Masse
(kg)
|
Dose
adminitrée (mg)
|
Lou
|
5
ans
|
1,05
|
17,5
|
50
|
Joé
|
15
ans
|
1,50
|
50
|
100
|
1. La
posologie a-t-elle été respectée pour Joé ? Justifier la réponse.
Non, la dose ne doit pas dépasser 70 mg / jour.
2. Vérifier que la
surface corporelle de Lou est environ de 0,71 m2.
Racine carrée [105×17,5 / 3600 ] ~0,71 m2.
3.
La posologie a-t-elle été respectée pour Lou ? Justifier la réponse
70 mg par m2 soit 70 x0,71 ~49,7 mg. La posologie est
respectée, l'écart relatif (50-19,7) / 49,7 x100 =0,6 % est très
faible. .
.
|
|