Mathématiques,
Brevet des collèges Polynésie 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM.
1. (15 - 9 x10-3)
/ (5 x102) =14,991x 10-2 / 5 = 2,9982 10-2
= 29,982 10-3 ; réponse B.
2. Combien faut-il
de temps pour parcourir 800 m à la vitesse moyenne de 40 km/h ?
Temps ( heure)=distance ( km ) / vitesse ( km /h) = 0,800 / 40 = 0,02
heure ou 0,02 x60 = 1,2 min ou 1 min 12 s. Réponse A.
3. Si on triple
l’arête d’un cube alors par combien est multiplié le volume du cube ?
V = a3 ; V' = (3a)3 = 27 a3 = 27 V.
Réponse C.
4. Quelle est
l’expression factorisée de 25x2−16 ?
(5x)2-42 = (5x-4) (5x+4). Réponse C.
Exercice 2.
1. Calcule PGCD(405
; 315). Précise la méthode utilisée et indique les calculs.
Algorithme d'Euclide : 405 = 315 +90 ; 315 = 3 x90 + 45 ; 90 = 2 x45.
Autre méthode :: 405 =34 x5 ; 315 =32 x5 x7.
le PGCD de 405 et 315 est 45.
2. Dans les bassins
d’eau de mer filtrée d’une ferme aquacole de bénitiers destinés à
l’aquariophilie, on compte 9 bacs contenant chacun 35 bénitiers de 12,5
cm et 15 bacs contenant chacun 27 bénitiers de 17,5 cm. L’exploitant
souhaite répartir la totalité des bénitiers en des lots de même
composition :
Par lot, même nombre de bénitiers de 12,5 cm et même nombre de
bénitiers de 17,5 cm.
a. Quel est le plus
grand nombre de lots qu’il pourra réaliser ? Justifie ta réponse.
9 x35=315 bénitiers de 12,5 cm et 15 x27 = 405 bénitiers de 17,5 cm.
PGCD(405 ; 315) = 45. Il peut réaliser 45
lots.
b. Quelle sera la
composition de chaque lot ?405 / 45 = 9 bénéitiers de 17,5 cm.
315 / 45 = 7 bénitiers de 12,5 cm.
|
|
|
Exercice 3.
Dans
l’Océan Pacifique Nord, des déchets plastiques qui flottent se sont
accumulés pour constituer une poubelle géante qui est, aujourd’hui,
grande comme 6 fois la France.
1. Sachant que la
superficie de la France est environ 550 000 km2, quelle est
la superficie actuelle de cette poubelle géante ?
6 x550 000 = 3 300 000 km2.
2. Sachant que la
superficie de cette poubelle géante augmente chaque année de 10 %,
quelle sera sa superficie dans un an ?
3 300 000 x1,1 = 3 630 000 km2.
3. Que penses-tu
de l’affirmation « dans 4 ans, la superficie de cette poubelle aura
doublé » ? Justifie ta réponse.
Superficie de la poubelle dans 4 ans :
3 300 000 x1,14 = 1,464 x 3 300 000 km2.
La superficie aura été multipliée par
1,464 et non pas par 2.
Exercice 4.
1. Construis un
triangle ABC rectangle en C tel que AB = 10 cm et AC = 8 cm.
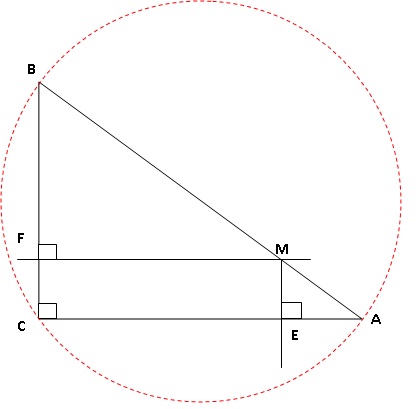
2. Calcule la
longueur BC (en justifiant précisément).
AB2 =AC2 + BC2 ; BC2 = AB2 -AC2 = 102 -82 = 36 ; BC = 6 cm.
3. a. Place le point M de
l’hypoténuse [AB] tel que AM= 2 cm.
b. Trace la
perpendiculaire à [AC] passant par M. Elle coupe [AC] en E.
c. Trace la
perpendiculaire à [BC] passant par M. Elle coupe [BC] en F.
d. À l’aide des
données de l’exercice, recopie sur ta copie la proposition que l’on
peut directement utiliser pour prouver que le quadrilatère MFCE est un
rectangle.
Proposition 1
: Si un quadrilatère a 4 angles droits alors c’est un rectangle.
Proposition 2
: Si un quadrilatère est un rectangle alors ses diagonales ont la même
longueur.
Proposition 3
: Si un quadrilatère a 3 angles
droits alors c’est un rectangle.
|
|
|
|
Exercice 5.
Pour cet exercice, on
utilise uniquement la courbe donnée ci-dessous qui représente une
fonction f .
En laissant apparaître les tracés utiles sur le graphique ci-dessous :
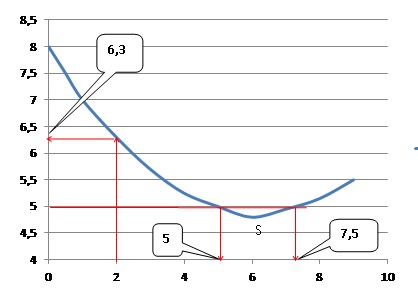
1. Donne une valeur
approchée de f (2).
2. Donne l’(ou les)
antécédent(s) de 5 par la fonction f .
3. Place, sur la
courbe de la fonction f un point S qui te semble avoir la plus petite
ordonnée.
4. Par lecture
graphique, donne des valeurs approchées des coordonnées de ton point S.
S( 6,3 ; 4,8).
Exercice 6.
Sur
un parking, une commune veut regrouper 6 conteneurs à déchets du même
modèle A ou B. Les deux modèles sont fabriqués dans le même matériau
qui a partout la même épaisseur.
- l e conteneur A est un pavé droit à base carrée de côté 1 m, et de
hauteur 2 m
- le conteneur B est constitué de deux demi-sphères de rayon 0,58 m et
d’un cylindre de même rayon et de hauteur 1,15 m
1. a. Vérifie que
les 2 conteneurs ont pratiquement le même volume.
VA = Aire base carrée x hauteur = 12 x2 = 2 m3.
VB = volume du cylindre + volume de la sphère.
VB =aire de base x hauteur + 4 / 3 p R3 = p R2 H + 4 / 3 p R3 = p R2 ( H + 4 / 3
R = 3,14 x0,582 (1,15 +4 / 3 x0,58) ~2,03 m3.
b. Quels peuvent
être les avantages du conteneur A ?
Plus stable, plus facile à fabriquer, plus facile à nettoyer.
2. On souhaite
savoir quel est le conteneur le plus économique à fabriquer.
a. Calcule l’aire
totale des 6 faces du conteneur A.
2 aire base carrée + 4 aire d'une face = 2 +4 x1 x 2 = 10 m2.
b. Vérifie que,
pour le conteneur B, l’aire totale, arrondie à 0,1 m2 près,
est 8,4 m2.
Aire latérale du cylindre + aire de la sphère = 2pR x H + 4 pR2 = 2pR( H +2R) =2
x3,14x0,58(1,15 +2x0,58) ~8,4 m2.
c. Quel est le
conteneur le plus économique à fabriquer ? Justifie ta réponse.
Le conteneur B nécessite moins de matière. ( même matériau et même
épaisseur).
|
|
Exercice 7. Calcule la hauteur du
cocotier.
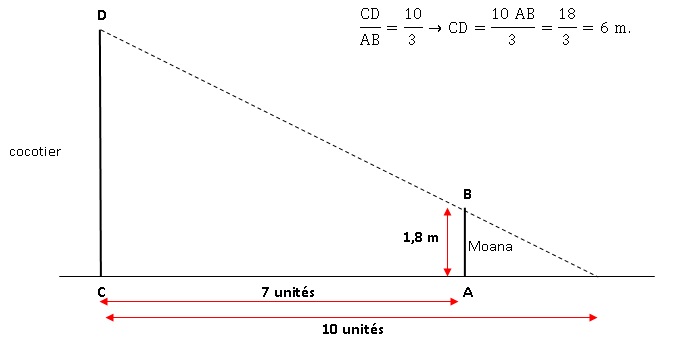
Exercice 8.
Soit
l’expérience aléatoire suivante :
- tirer au hasard une boule noire, noter son numéro ;
- tirer au hasard une boule blanche, noter son numéro ;
- puis calculer la somme des 2 numéros tirés.
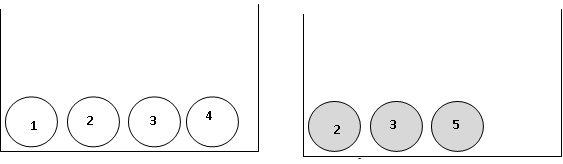
1. On a simulé
l’expérience avec un tableur, en utilisant la fonction ALEA() pour
obtenir les numéros des boules tirées au hasard.
Voici les résultats des premières expériences :
|
A
|
B
|
C
|
D
|
1
|
Expériennce
|
Numéro
de la boule noire
|
Numéro
de la boule blanche
|
Somme
|
2
|
n°1
|
4
|
2
|
6
|
3
|
n°2
|
1
|
2
|
3
|
4
|
n°3
|
2
|
3
|
5
|
5
|
n°4
|
3
|
3
|
6
|
6
|
n°5
|
3
|
5
|
8
|
7
|
n°6
|
4
|
3
|
7
|
a. Décris
l’expérience n° 3.
La boule noire tirée porte le numéro 2 ; la boule balanche tirée porte
le numéro3 ; la somme vaut 5.
b. Parmi les 4
formules suivantes, recopie sur ta feuille celle qui est écrite dans la
case D5 :
2⋆A4 ; =B4+C4 ; = B5+C5
vrai
; = SOMME(D5)
c. Peut-on obtenir
la somme 2 ? Justifie.
Non : le plus petit numéro d'une boule noire est égal à 2 et le plus
petit numéro d'une boule blanche est égal à 1.
d. Quels sont les
tirages possibles qui permettent d’obtenir la somme 4 ? Quelle est la
plus grande somme possible ? Justifie.
1 (blanc )+3 ( noire) et 2 (
blanc) +2 (noire).
La plus grande somme possible est 4 ( blanc) + 5 (noire) = 9.
2. Sur une seconde
feuille de calcul, on a copié les résultats obtenus avec 50
expériences, avec 1 000 expériences, avec 5 000 expériences et on a
calculé les
fréquences des différentes sommes.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Somme
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Effectif
total
|
2
|
Effectif
|
5
|
10
|
9
|
8
|
8
|
8
|
2
|
50
|
3
|
Fréquence
|
0,1
|
0,2
|
0,18
|
0,16
|
0,16
|
0,16
|
|
|
4
|
|
|
|
|
|
|
|
|
|
5
|
Somme
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Effectif
total
|
6
|
Effectif
|
79
|
161
|
167
|
261
|
166
|
72
|
94
|
1000
|
7
|
Fréquence
|
0,079
|
0,161
|
0,167
|
0,261
|
0,166
|
0,072
|
0,094
|
|
8
|
|
|
|
|
|
|
|
|
|
9
|
Somme
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Effectif
total
|
10
|
Effectif
|
405
|
844
|
851
|
1221
|
871
|
410
|
398
|
5000
|
11
|
Fréquence
|
0,081
|
0,1688
|
0,1702
|
0,2442
|
|
0,1742
|
0,082
|
0,0796
|
a. Quelle est la
fréquence de la somme 9 au cours des 50 premières expériences ?
Justifie.
2 / 50 = 0,04.
b. Quelle formule
a-t-on écrite dans la case B7 pour obtenir la fréquence de la somme 3 ?
=B6/1000 ou = B6/$I6
c. Donne une
estimation de la probabilité d’obtenir la somme 3.
0,081 ; un tirage favorable sur 12 tirages possibles ; 1/12=0,083.
.
|
|