Mathématiques, Brevet des collèges Métropole 09 / 2013

Mathématiques, Brevet des collèges Métropole 09 / 2013

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

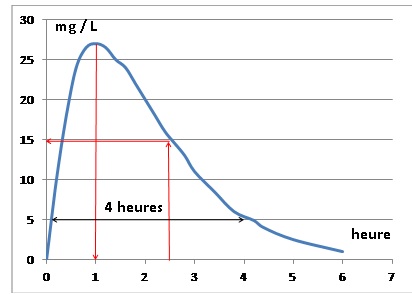
Exercice 1.
Lorsqu’on absorbe un médicament, la quantité de principe actif de ce médicament dans le sang évolue en fonction du temps.Cette quantité se mesure en milligrammes par litre de sang.
Le graphique ci-dessous représente la quantité de principe actif d’un médicament dans le sang, en fonction du temps écoulé, depuis la prise de ce médicament.
Répondre aux questions suivantes à partir de lectures graphiques. Aucune justification
n’est demandée dans cet exercice.
1. Au bout de combien de temps la quantité de principe actif de médicament dans le sang est-elle maximale ? 1 heure.
2. Quelle est la quantité de principe actif de médicament dans le sang au bout de 2 h 30 min?
15 mg/L.
3. Pour que le médicament soit efficace, la quantité de principe actif de médicament dans le sang doit être supérieure à 5mg/L. Pendant combien de temps le médicament est-il efficace ? 4 heures.

.
.

Exercice 2.
Tom lance cinquante fois deux dés à six faces parfaitement équilibrés. Il note dans une feuille de calcul les sommes obtenues à chaque lancer. Il obtient le tableau suivant :

B3
=B2/M2

A
B
C
D
E
F
G
H
I
J
K
L
M
N

1
Somme obtenue
2
3
4
5
6
7
8
9
10
11
12
Total

2
Nombre d'apparitions
3
1
4
6
9
9
7
3
5
3
0
50

3
Fréquence d'apparition
0,06

1. Quelle formule a-t-il saisie dans la cellule M2 pour vérifier qu’il a bien relevé 50 résultats ?
=SOMME(B2:L2)
2. Tom a saisi dans la cellule B3 la formule =B2/M2 . Il obtient un message d’erreur quand il la tire dans la cellule C3. Pourquoi ?
50 occupe une position fixe, il faut écrire : = B2/$M2.
Sinon, comme N3 contient zéro, on aboutit à une erreur " division par zéro".
3. Tom déduit de la lecture de ce tableau que s’il lance ces deux dés, il n’a aucune chance d’obtenir la somme 12. A-t-il tort ou raison ?
Il a tord, la sortie du double six est possible, il faudrait effectuer un plus grand nombre de lancers.

Exercice 3.
ABCD est un rectangle tel que AB = 30 cm et BC = 24 cm.
On colorie aux quatre coins du rectangle quatre carrés identiques en gris. On délimite ainsi un rectangle central que l’on colorie en noir.

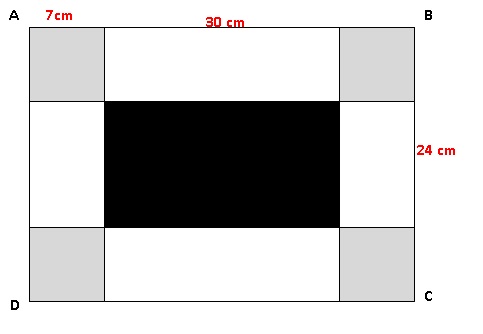
1. Dans cette question, les quatre carrés gris ont tous 7 cm de côté. Dans ce cas :
a. quel est le périmètre d’un carré gris ?
4 x7 = 28 cm.
b. quel est le périmètre du rectangle noir ?
Longueur : 30-7-7=16 cm ; largeur : 24-7-7 = 10 cm ; périmètre : 2(16+10) = 52 cm.
2. Dans cette question, la longueur du côté des quatre carrés gris peut varier.
Par conséquent, les dimensions du rectangle noir varient aussi.
Est-il possible que le périmètre du rectangle noir soit égal à la somme des périmètres des quatre carrés gris ? On appelle x la mesure du côté d'un carré gris.
Périmètre des 4 carrés gris : 4 * 4x = 16 x.
Périmètre du rectangle noir : 2(30-2x + 24-2x) = 108- 8x.
16 x = 108 -8x ; 24x = 108 ; x = 108 / 24 = 4,5 cm.

Exercice 4.
Un stage de voile pour enfant est proposé pendant les vacances. Le prix affiché d’un stage pour un enfant est de 115 €. Lorsqu’une famille inscrit deux enfants ou plus, elle bénéficie d’une réduction qui dépend du nombre d’enfants inscrits.
1. Une famille qui inscrit trois enfants paie 310,50 €. Pour cette famille, quel est, par enfant, le prix de revient d’un stage ?
310,50 / 3 = 103,5 €.
2. Compléter les deux factures suivantes. Aucune justification n’est attendue dans cette question.

Prix d'un stage
115 €

Prix d'un stage 115 €

Nombre d'enfants inscrits
2
Nombre d'enfants inscrits
3

Prix total avant réduction
230 €
Prix total avant réduction
345 €

Montant de la réduction
5% du prix total
230 x0,05
=11,5 €
Montant de la réduction
34,5 x100 / 345
= 10 %
345-310,5
=34,5 €

Prix à payer
230-11,5
=218,5 €

Prix à payer
310,50 €

.

.
.

Exercice 5.
Voici une figure codée réalisée à main levée :
La droite (AC) est perpendiculaire à la droite (AB).
La droite (EB) est perpendiculaire à la droite (AB).
Les droites (AE) et (BC) se coupent en D.
AC = 2,4 cm ; AB = 3,2 cm ; BD = 2,5 cm et DC = 1,5 cm.
1. Réaliser la figure en vraie grandeur sur la copie.
2. Déterminer l’aire du triangle ABE.

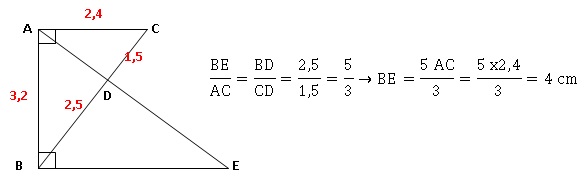
Aire du triangle ABE : BE x AB / 2 = 4 x3,2 / 2 = 6,4 cm².

Exercice 6.
On souhaite construire une structure pour un skatepark, constituée d’un escalier de six marches identiques permettant d’accéder à un plan incliné dont la hauteur est égale à 96 cm. Le projet de cette structure est présenté ci-dessous.

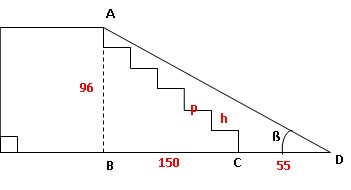
Normes de construction de l’escalier :
60 < 2h + p < 65 où h est la hauteur d’une marche et p la profondeur d’une marche, en cm.
Demandes des habitués du skate park :
Longueur du plan incliné (c’est-à-dire la longueur AD) comprise entre 2,20 m et 2,50 m.
Angle formé par le plan incliné avec le sol (ici l’angle� ß) compris entre 20° et 30°.
1. Les normes de construction de l’escalier sont-elles respectées ?
6h = 96 ; h = 96 / 6 =16 cm ; 5p =150 ; p = 150 / 5 = 30 cm.
2h+p = 2 x16 +30 = 62 cm, valeur comprise entre 60 et 65 cm. Les normes sont respectées.
2. Les demandes des habitués du skatepark pour le plan incliné sont-elles satisfaites ?
tan ß = AB / BD = 96 / (150 +55) = 96 / 205 ~0,4683 ; ß ~25,1 °, valeur comprise entre 20 et 30 °.
AD² = AB² + BD² = 96² +205² =51241 ; AD =226 cm = 2,26 m, valeur comprise entre 2,20 et 2,50 m.
Les demandes des habitués du skatepark pour le plan incliné sont satisfaites.

Exercice 7. Indiquer si les affirmations suivantes sont vraies ou fausses.
Rappel : toutes les réponses doivent être justifiées.
Affirmation 1 : « La vitesse moyenne d’un coureur qui parcourt 18 km en une heure est strictement supérieure à celle d’une voiture télécommandée qui parcourt 5 m
par seconde. » Faux.
18 / 3,6 = 5 m /s. les deux vitesse sont égales.
Affirmation 2 : « Pour tout nombre x, on a l’égalité : (3x −5)² = 9x² −25. » Faux.
(3x −5)² = 9x² +25 -30x.
Affirmation 3 : « Dans une série de données numériques, la médiane de la série est toujours strictement supérieure à la moyenne. »Faux.
Exemple de série : 2 ; 3 ; 5 ; 8 ; 10.
Moyenne : (2+3+5+8+10) /5 = 5,6 ; médiane : 5.

Exercice 8.
Flora fait des bracelets avec de la pâte à modeler. Ils sont tous constitués de 8 perles rondes (boule de diamètre 8 mm) et de 4 perles longues ( cylindre de hauteur 16 mm et de diamètre 8 mm ).
Cette pâte à modeler s’achète par blocs qui ont tous la forme d’un pavé droit dont les dimensions sont 2 x 6 x 6 cm³.
La pâte peut se pétrir à volonté et durcit ensuite à la cuisson.
Flora achète deux blocs de pâte à modeler : un bloc de pâte à modeler bleue pour faire les perles rondes et un bloc de pâte à modeler blanche pour faire les perles longues.
Combien de bracelets peut-elle ainsi espérer réaliser ?
Volume d'un bloc : V = 2 x 6 x6 = 72 cm³.
Volume d'un cylindre : p R² H = 3,14 x0,4² x1,6 ~0,80 cm³.
Nombre de perle longue : 72 / 0,80 =89,57 soit 89.
Volume d'une boule :4 / 3 p R³ = 4 / 3 x3,14 x0,4³ ~0,27 cm³.
Nombre de perle ronde : 72 / 0,27 =268,7 soit 268.
Elle peut réaliser 89 / 4 = 22,25 soit 22 bracelets, les perles rondes sont en large excès.
.

menu