Mathématiques, Brevet des collèges Nlle Calédonie 2013

Mathématiques, Brevet des collèges Nlle Calédonie 2013

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1. QCM
1. Une fourmi se déplace à :4 km/s ; 4 m/s ; 4 cm /s. Vrai.
2. La distance de la Terre à la Lune est : 3,844 10⁵ km. Vrai ; 3,844 10^-5 km ; 3,844 km.
3 Une écriture simplifiée de 125 / 625 est 1 / 6 ; 1 / 5, vrai ; 125,625.
625 = 5 x125.
4. racine carrée de 12 est égal à : 6 ; 4 racine carrée (3) ; 2 racine carrée (3). Vrai.
racine carrée (4 x3 ) racine carrée (4) x racine carrée (3).

Exercice 2.
Un enfant a ramassé 20 coquillages.
Les grands mesurent 2 cm de long, les petits mesurent 1 cm.
Tous les coquillages mis bout à bout font 32 cm au total.
Combien a-t-il de grands coquillages et combien de petits ?
On appelle : x le nombre de petis coquillages.
x +2(20-x) = 32 ; x +40 -2x = 32 ; 40-32 = x ; x = 8
8 petis coquillages et 12 grands coquillages.

.
.

Exercice 3.
Un restaurant propose cinq variétés de pizzas, voici leur carte :
CLASSIQUE : tomate, jambon, oeuf, champignons
MONTAGNARDE : crème, jambon, pomme de terre, champignons
LAGON : crème, crevettes, fromage
BROUSSARDE : crème, chorizo, champignons, salami
PLAGE : tomate, poivrons, chorizo
1. Je commande une pizza au hasard, quelle est la probabilité qu’il y ait des champignons dedans?
3 cas favorables sur 5 ; 3 / 5 = 0,6.
2. J’ai commandé une pizza à la crème, quelle est la probabilité d’avoir du jambon?
1 cas favorable sur 3 ; 1 /3 ~0,33.
3. Il est possible de commander une grande pizza composée à moitié d’une variété et à moitié d’une autre. Quelle est la probabilité d’avoir des champignons sur toute la pizza ? On pourra s’aider d’un arbre des possibles.

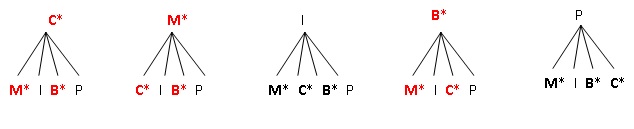
6 cas favorables sur 20 possibilités : 6 / 20 = 3 / 10 = 0,3.
4. On suppose que les pizzas sont de forme circulaire. La pizzeria propose deux tailles :
moyenne : 30 cm de diamètre ; grande : 44 cm de diamètre.
Si je commande deux pizzas moyennes, aurai-je plus à manger que si j’en commande une grande ? Justifier la réponse.
Aire d'e deux pizzas moyennes : 2 x p R² =2 x 3,14 x15²=1413 cm².
Aire d'une grande : 3,14 x22² ~1520 cm².
J'aurai plus à manger si je commande une grande pizza.

Exercice 4.
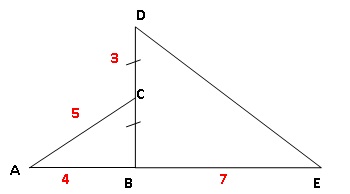
Sur le dessin ci-contre, les points A, B et E sont alignés, et C le milieu de [BD].

1. Quelle est la nature du triangle ABC ? Justifier.
AC² =25 ; AB² +BC² = 16+9 = 25.
AC² =AB² +BC² ;
d'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.
2. En déduire la nature du triangle BDE.
(BD) est perpendiculaire à (AE). Le triangle BDE est rectangle en B.
3. Calculer ED. Arrondir le résultat au dixième.
DE² =DB² +BE² =6² +7² = 36 +49 = 85 ; DE ~9,2 cm.

.
.

Exercice 5.
En se retournant lors d’une marche arrière, le conducteur d’une camionnette voit le sol à 6 mètres derrière son camion.
Sur le schéma, la zone grisée correspond à ce que le conducteur ne voit pas lorsqu’il regarde en arrière.

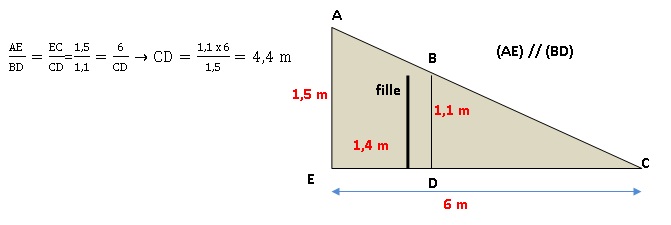
1. Calculer DC.
2. En déduire que ED = 1,60 m.
ED = EC -DC = 6 -4,4 = 1,6 m.
3. Une fillette mesure 1,10 m. Elle passe à 1,40 m derrière la camionnette. Le conducteur peut-il la voir ? Expliquer.
le conducteur ne peut pas la voir ( schéma ci-dessus).

Exercice 6.
Un vendeur de bain moussant souhaite faire des coffrets pour les fêtes de fin d’année.
En plus du traditionnel « pavé moussant », il veut positionner par dessus une « pyramide moussante » qui ait le même volume que le pavé.

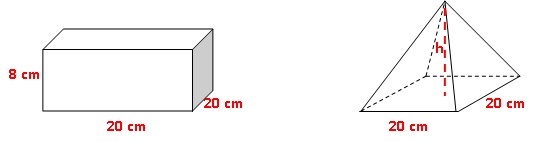
1. Calculer le volume d’un « pavé moussant ».
aire de la base carrée x hauteur = 20 x 20 x8 =3200 cm³.
2. Montrer que le volume d’une « pyramide moussante » est égal à 400h /3 cm³.
Aire de la pyramide : aire de la base carrée x hauteur / 3 = 400 h / 3 cm³.
3. En déduire la hauteur qu’il faut à une pyramide pour qu’elle ait le même volume qu’un pavé.
400 h / 3 = 3200 ; h = 3200 x 3 / 400 = 24 cm.

Exercice 7.
L’épreuve du concours australien de mathématiques est divisée en trois catégories :
• « Junior » qui regroupe les classes de 5e et 4e
• « Intermédiaire » pour les classes de 3e et 2nde
• « Senior » avec les classes de 1re et de terminale.
Cette année 25 établissements se sont inscrits. Plus de 3 000 élèves, répartis comme l’indique le tableau suivant, ont participé à ce concours.
1. Compléter le tableau. Les cases barrées ne sont pas à remplir.

A
B
C
D
E
F
G

1
catégorie
Junior
Intermédiaire
Sénior

2
Effectif par catégorie

1958

876

308

3
Niveau
5e
4e
3e
2nde
1ere
term

4
Effectif par niveau
989
969
638
238
172
136

5
Effectif total
3142

308-172=136.
638+238=876.
1958 +876 +308 = 3142.
2. Quel est le niveau où il y a le plus d’inscrits ? 5e.
3. Quelle est la catégorie ayant le moins d’inscrits ? Sénior.
4. En moyenne, combien d’élèves par établissement ont participé ? Arrondir à l’unité.
3142 / 25 ~126.
5. Le tableau est une copie d’écran d’un tableur.
Quelle formule faut-il écrire dans la case G5 pour obtenir l’effectif total ?
=C2+E2+G2 ou = SOMME(B4:G4).

Exercice 8.
Dans un jeu vidéo on a le choix entre trois personnages : un guerrier, un mage et un chasseur.
La force d’un personnage se mesure en points.
Tous les personnages commencent au niveau 0 et le jeu s’arrête au niveau 25.
Cependant ils n’évoluent pas de la même façon :
Le guerrier commence avec 50 points et ne gagne pas d’autre point au cours du jeu.
Le mage n’a aucun point au début mais gagne 3 points par niveau.
Le chasseur commence à 40 points et gagne 1 point par niveau.
1. Au début du jeu, quel est le personnage le plus fort ? Et quel est le moins fort ?
Le guerrier est le plus fort ; le mage est le moins fort.
2. Compléter le tableau suivant.

Niveau
0
1
5
10
15
25

Points du guerrier
50
50
50
50
50
50

Points du mage
0
3
5 x3 = 15
10 x3 = 30
15 x3 = 45
25 x3 = 75

Points du chasseur
40
41
40+5=45
40+10=50
40+15=55
40+25=65

3. À quel niveau le chasseur aura-t-il autant de points que le guerrier ? Niveau 10.
4. Dans cette question, x désigne le niveau de jeu d’un personnage.
Associer chacune des expressions suivantes à l’un des trois personnages :
chasseur, mage ou guerrier :
• f (x) = 3x ; mage.
• g (x) = 50 ;guerrier.
• h(x) = x +40. Chasseur.
5. Dans le repère, la fonction g est représentée.
Tracer les deux droites représentant les fonctions f et h.

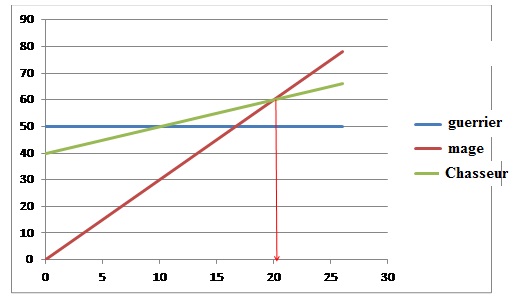
6. Déterminer à l’aide du graphique, le niveau à partir duquel le mage devient le plus fort.
Le mage devient le plus fort à partir du niveau 21.

menu