Mathématiques,
Brevet des collèges Pondichéry 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Emma et Arthur ont acheté pour leur mariage 3 003 dragées au chocolat
et 3 731 dragées aux amandes.
1. Arthur propose
de répartir ces dragées de façon identique dans 20 corbeilles. Chaque
corbeille doit avoir la même composition. Combien lui reste-t-il de
dragées non utilisées ?
3000 et 3720 sont des multiples de 20. Il restera 3 dragées au chocolat
et 11 dragées aux amandes. Chaque corbeille compte 3000 / 20 = 150
draghées au chocolat et 3720 / 20 =186 dragées aux amandes.
2. Emma et Arthur
changent d’avis et décident de proposer des petits ballotins dont la
composition est identique. Ils souhaitent qu’il ne leur reste pas de
dragées.
a. Emma propose
d’en faire 90. Ceci convient-il ? Justifier.
3003 = 90 x33 + 33 ; 3731 =41 x90 +41.
Cela ne convient pas, il reste 33 dragées au chocolat et 41 dragées aux
amandes.
b. Ils se mettent
d’accord pour faire un maximum de ballotins. Combien en feront-ils et
quelle sera leur composition ?
3003 = 3 x7 x11 x 13 ; 3731 = 7 x13 x 41.
Le PGCD de 3003 et 3731 est 7 x13 = 91. Ils feront 91 ballotins
contenant chacun 3003/91 = 33 dragées au chocolat et 3731 / 91 = 41
dragées aux amandes.
Exercice 2. QCM
|
A
|
B
|
C
|
| racine
carrée ( (-5)2) |
n'existe
pas
|
est
égale à -5
|
est égale à 5
|
Si
deux surfaces ont la même aire
|
elles
sont superposables
|
elles
ont le même périmètre
|
leurs périmètres ne sont pas forcément égaux.
|
f(x)
= 3x-(2x+7)+(3x+5)
|
f est affine
3x-2x-7+3x+5
=4x-2
|
f
est linéaire
|
f
n'est pas affine
|
Hicham
a récupéré les résultats d'une enquète sur les n° sortis ces dernières
années au loto. Il souhaite jouer lors du prochain tirage.
|
il
vaut mieux jouer les n° qui sont souvent sortis
|
il
vaut mieux jouer les numéros qui ne sont pas sortis
|
l'enquète ne peut pas l'aider.
|
Une
expression factorisée de
(x-1)2-16 est
|
(x+3)(x-5)
(x-1+4)(x-1-4)
|
(x-4)(x+4)
|
x2-2x-15
|
.
|
|
|
Exercice 3.
« Je prends un nombre entier. Je lui ajoute 3 et je
multiplie le résultat par 7. J’ajoute le
triple du nombre de départ au résultat et j’enlève 21. J’obtiens
toujours un multiple de 10. »
Est-ce vrai ? Justifier.
Le
nombre de départ est noté n.
n+3
(n+3) x7
(n+3) x7+3n
(n+3) x7 +3n-21
7n +21 +3n-21 = 10n, multiple de 10.
Exercice 4.
Une commune
souhaite aménager des parcours de santé sur son territoire. On fait
deux propositions au conseil municipal, schématisées ci-dessous :
• le parcours ACDA
• le parcours AEFA
Ils souhaitent faire un parcours dont la longueur s’approche le plus
possible de 4 km.
Peux-tu les aider à choisir le parcours ? Justifie.
La figure ci-dessous n'est pas à l'échelle.
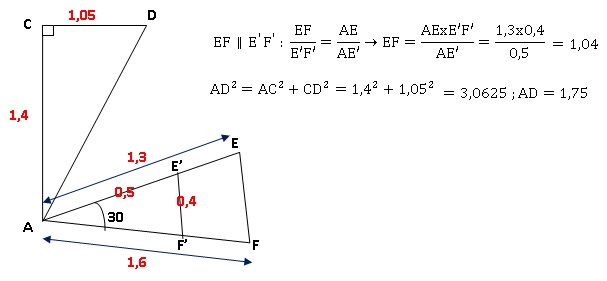
Parcours ACDA : 1,4 +1,05+1,75 =4,2 km.
Parcours AEFA : 1,3 +1,04 +1,6 = 3,94 km. Ce parcours est choisi.
|
|
|
|
Exercice 5.
Pense-bête : toutes les formules données ci-dessous correspondent bien
à des formules d’aires ou de volumes. On ne sait pas à quoi elles
correspondent, mais elles peuvent quandmême être utiles pour résoudre
l’exercice ci-dessous.
aire de base x hauteur / 3 ; pr2
; 4 / 3 pr3 ; aire
de base x hauteur.
Voici une bouteille constituée d’un cylindre et d’un tronc de cône
surmonté par un goulot cylindrique. La bouteille est pleine lorsqu’elle
est remplie jusqu’au goulot.
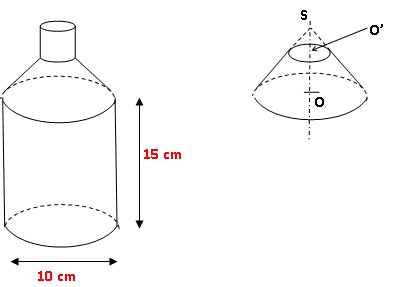
1. Calculer le
volume exact de la partie cylindrique de la bouteille puis en donner un
arrondi au cm3.
aire de base x hauteur = p
r2 h = p
52x15 = 375 p
~1178 cm3.
2. Pour obtenir le
tronc de cône, on a coupé un cône par un plan parallèle à la base
passant par O′. La hauteur SO du grand cône est de 6 cm et la hauteur
SO’ du petit est égale à 2 cm. Le rayon de la base du grand cône est de
5 cm.
a. Calculer le
volume V1 du grand cône de hauteur SO (donner la valeur
exacte).
aire de base x hauteur /3= p
r2 h /3 = 3,14x 52x 6 / 3 = 50 p cm3.
b. Montrer que le
volume V2 du tronc de cône est égal à 1300 p / 27 cm3. En
donner une valeur arrondie au cm3.
Les dimensions du petit cône sont celles du grand cône divisées par 3.
Le volume du petit cône est égal à celui du grand cône divisé par 33
=27.
Volume du tronc de cône : V1-V2 avec V2
= V1 / 27 ; V1-V2 = 26 V1 /
27 = 26 x50 p /
27 = 1300 p / 27
~151 cm3.
3. Parmi les
quatre graphiques ci-dessous, l’un d’entre eux représente le volume V
(h) de la bouteille en fonction de la hauteur h de remplissage du
bidon. Quel est ce graphique ? Pourquoi les autres ne sont-ils pas
convenables ?
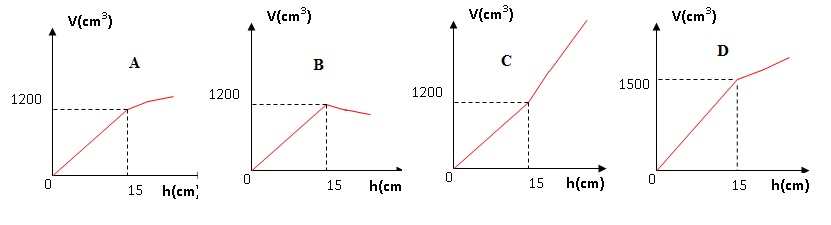
A convient.
B ne convient pas : décroissance du volume après h = 15 cm.
C ne convient pas : croissance trop rapide du volume après h = 15 cm.
D ne convient pas : le volume 1500 pour h = 15 ccm, ne correpond pas
aux calculs précédents
|
|
Exercice 6.
Voici
le classement desmédailles d’or reçues par les pays participant aux
jeux olympiques pour le cyclisme masculin.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
N
|
O
|
1
|
Nombre
médaille d'or
|
1
|
2
|
3
|
4
|
5
|
6
|
11
|
13
|
14
|
15
|
18
|
32
|
40
|
|
2
|
Effectif
|
8
|
2
|
2
|
2
|
1
|
3
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
26
|
Quelle formule a-t-on saisie dans la
cellule O2 pour obtenir le nombre total de pays ayant eu une médaille
d’or ?
=SOMME(B1:N1) ( on trouve 164).
2. a. Calculer la
moyenne de cette série (arrondir à l’unité).
(1*8 +2*2 +3*2 +4*2 +5 +6*3 +11 +13*2 +14+15+18+32+40) / 26 ~8.
b. Déterminer la
médiane de cette série.
L'effectif tootal étant de 26, la médiane est la moyenne de la 13e
et de la 14e valeur de la série soit 4.
c. En observant les
valeurs prises par la série, donner un argument qui explique pourquoi
les valeurs de la moyenne et de la médiane sont différentes.
Les valeurs de la série sont très dispersées. Un grand nombre de pays
obtient peu de médailles et un très petit nombre en obtient beaucoup.
3. Pour le cyclisme
masculin, 70% des pays médaillés ont obtenu au moins une médaille d’or.
Quel est le nombre de pays qui n’ont obtenu que des médailles
d’argent ou de bronze (arrondir le résultat à l’unité) ?
Nombre de pays médaillés or : 26 ; nombre total de pays médaillés : 26
/ 0,70 ~ 37.
Nombre de pays médaillés argent ou bronze : 37-26
= 11. |
|