Mathématiques,
Brevet des collèges Amérique du nord 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM
Exercice 2. QCM
Pour amortir les chocs contre les autres embarcations ou le quai, les
péniches sont équipées de «
boudins » de protection. Calculer
le volume exact en cm3 du «boudin»de protection ci-dessous,
puis arrondir au centième.
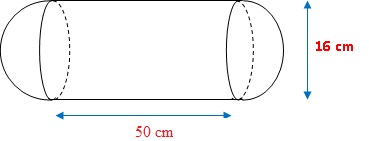
Volume du cylindre : pr2h
= p 82
x50 =3200 p cm3.
Volume de la sphère : 4 / 3 pr3 =4 / 3 p 83 =2048 / 3 p cm3.
Total : (3200 x3 +2048) / 3 p=11648 / 3 p~12 197,76 cm3.
|
|
|
Exercice 3.
1.
La longueur du Canal du Midi est de 240 km de Toulouse à l’étang de
Thau et la vitesse des embarcations y est limitée à 8 km/h. Combien de
temps, au moins, faut-il pour effectuer ce trajet en péniche sans faire
de pause ?
240 / 8 = 30 heures.
2. On assimilera
une écluse à un pavé droit de 8,4 m de large, de 30 m de long et de 3m
de hauteur.
Calculer le volume de cette écluse.
8,4 x30 x3 =756 m3.
3. Le prix
hebdomadaire de la location d’un bateau à moteur dépend de la période.
Il est de 882 € du 01/01/2014 au 28/04/2014.
Il augmente de 27% pour la période du 29/04/2014 au 12/05/2014.
Calculer le prix de la location pour cette période.
882 x1,27 =1120,14 €.
Exercice 4.
Durant
un parcours sur le Canal du Midi partant de l’écluse de Renneville
jusqu’à l’écluse de Gay, on a relevé les hauteurs de chaque écluse
franchie depuis le départ dans une feuille de calcul.
Les hauteurs franchies de manière ascendante sont notées positivement,
celles de manière descendante négativement.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
K
|
L
|
M
|
1
|
écluse
|
Renneville
|
Encasan
|
Embrel
|
Bord
|
Méditeranée
|
Roc
|
Laurens
|
Domergue
|
Planque
|
St
Roch
|
Gay
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
hauteur
(m)
|
2,44
|
4,85
|
3,08
|
2,62
|
-2,58
|
-5,58
|
-6,78
|
-2,24
|
-2,63
|
-9,42
|
-5,23
|
|
1. Quelle formule doit-on saisir
dans la cellule M3 pour obtenir la valeur du dénivelé du parcours ?
=SOMME(B3:L3)
2. Quelle est la
valeur du dénivelé du parcours ?
2,44 +4,85 +3,08 +2,62 -2,58 -5,58 -6,78 -2,24 -2,63 -9,42 -5,23=
-21,47 m.
3. Le parcours
est-il, globalement, ascendant ou descendant ?
De Renneville à Bord, le parcours est ascendant, puis descendant par la
suite.
Le dénivellé étant négatif, le parcours est globalement descendant.
|
|
|
|
Exercice 5.
Pour
une bonne partie de pêche au bord du canal, il faut un siège pliant
adapté ! Nicolas est de taille moyenne et pour être bien assis, il est
nécessaire que la hauteur de l’assise du siège soit comprise entre 44
cm et 46 cm. La hauteur de ce siège lui est-elle adaptée ?
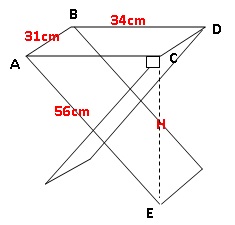
H2 = AE2 -AC2 = 562 -342
=1980 ; H = 44,5 cm, valeur comprise entre 44 et 46 cm. Le siège
est bien adapté.
Exercice 6.
Pendant le remplissage d’une écluse, Jules et Paul, à bord de leur
péniche, patientent en jouant aux dés. Ces dès sont équilibrés.
1. Est-ce que, lors
du jet d’un dé, la probabilité d’obtenir un « 1 » est la même que celle
d’obtenir un « 5 » ? Expliquer.
Oui, la probabilité d'obtenir 1 est égale à celle d'obtenir 5, c'est à
dire 1 /6, si le dé n'est pas truqué.
2. Jules lance en
même temps un dé rouge et un dé jaune. Par exemple il peut obtenir 3 au
dé rouge et 4 au dé jaune, c’est l’une des issues possibles. Expliquer
pourquoi le nombre d’issues possibles quand il lance ses deux dés est
de 36.
Chaque dé comporte 6 faces. Lors du lancer de deux dés, il y a 6 x6 =
36 issues possibles.
Jules propose à Paul de jouer avec ces deux dés (un jaune et un rouge),
Il lui explique la règle :
- Le gagnant est le premier à remporter un total de 1000 points.
- Si, lors d’un lancer, un joueur fait deux « 1 », c’est-à-dire une
paire* de « 1 », il remporte 1 000 points (et donc la partie).
- Si un joueur obtient une paire de 2, il obtient 100 fois la valeur du
2, soit 2×100 = 200 points.
- De même, si un joueur obtient une paire de 3 ou de 4 ou de 5 ou 6, il
obtient 100 fois la valeur du dé soit 3×100 = 300, ou . . .
- Si un joueur obtient un résultat autre qu’une paire (exemple 3 sur le
dé jaune et 5 sur le dé rouge), il obtient 50 points.
* On appelle une paire de 1 quand on obtient deux 1, une paire de 2
quand on obtient deux 2 . . .
3. Paul a déjà fait
2 lancers et a obtenu 650 points.
Quelle est la probabilité qu’il gagne la partie à son troisième lancer ?
Il doit marquer au moins 350 points.
Soit une paire de 1, une paire de 4, une paire de 5 ou une paire
de 6.
Probabilité d'obtenir une paire de chiffres ; 1 / 36.
Probabilité de gagner : 1 /36 +1/36 +1/36 +1/36= 4 /36 = 1/9.
|
|
Exercice 7.
On
étudie plus précisément le remplissage d’une écluse pour faire passer
une péniche de l’amont vers l’aval.
Principe : Il s’agit de faire monter le niveau de l’eau dans l’écluse
jusqu’au niveau du canal en amont afin que l’on puisse ensuite faire
passer la péniche dans l’écluse.
Ensuite, l’écluse se vide et le niveau descend à celui du canal en
aval. La péniche peut sortir de l’écluse et poursuivre dans le canal en
aval.
h = 4,3 m ; x = 1,8 m.
La vitesse de l’eau s’écoulant par la vantelle (vanne) est donnée par
la formule suivante v = racine carrée ( 2g(h-x)).
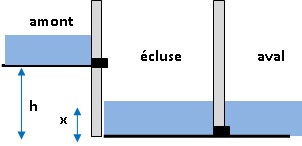
où g = 9,81 (accélération en mètre par seconde au carré noté m.s−2)
et v est la vitesse (en mètre par seconde noté m.s−1)
1. Calculer
l’arrondi à l’unité de la vitesse de l’eau s’écoulant par la vantelle à
l’instant de son ouverture. (On considère l’ouverture comme étant
instantanée).
v = raccine carré (2 x9,81 (4,3-1,8)) = 7,0 m s-1.
2. Pour quelle
valeur de x, la vitesse d’écoulement de l’eau sera-t-elle nulle ? Qu’en
déduit-on pour le niveau de l’eau dans l’écluse dans ce cas ?
Le niveau de l'eau dans l'écluse est égal au niveau de l'eau en
amont soit x = h = 4,3 m.
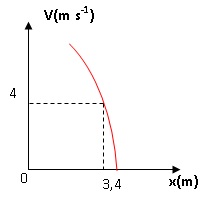
3. Le graphique
donné représente la vitesse d’écoulement de l’eau par la vantelle en
fonction du niveau x de l’eau dans l’écluse.
Déterminer, par lecture graphique, la vitesse d’écoulement lorsque la
hauteur de l’eau dans l’écluse est de 3,4 m.
Exercice 8.
Le débit moyen q d’un fluide dépend de la vitesse moyenne v du fluide
et de l’aire de la section d’écoulement d’aire S. Il est donné par la
formule suivante :
q = S ×v
où q est exprimé en m3.s−1 ; S est exprimé en m2
; v est exprimé en m.s−1.
Pour cette partie, on considérera que la vitesse moyenne d’écoulement
de l’eau à travers la vantelle durant le remplissage est v = 2,8 m.s−1.
La vantelle a la forme d’un disque de rayon R = 30 cm.
1. Quelle est
l’aire exacte, en m2, de la vantelle ?
S =pR2
= 0,32p
= 0,09 p m2.
2. Déterminer le
débit moyen arrondi au millième de cette vantelle durant le remplissage.
q = S v = 0,09 x3,141 x2,8 =0,792 m3 s-1.
3. Pendant combien
de secondes, faudra-t-il patienter pour le remplissage d’une écluse de
capacité 756 m3 ? Est-ce qu’on attendra plus de 15 minutes ?
756 /0,792 ~955 s ou 15 min 55 s, valeur supérieure à 15 min.
Exercice 9.
Certaines écluses ont des portes dites « busquées » qui forment un
angle pointé vers l’amont de manière à résister à la pression de l’eau,
En vous appuyant sur le schéma ci-dessus, déterminer la longueur des
portes au cm près.
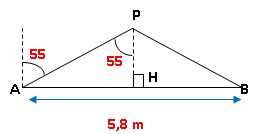
sin 55 = AH / AP ; AP = AH / sin 55 = 2,9 / 0,81915 ~3,54 m.
|
|