Mathématiques,
Brevet des collèges Métropole 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
|
Exercice 1.
Voici un octogone régulier ABCDEFGH.
1. Représenter un
agrandissement de cet octogone en l’inscrivant dans un cercle de rayon
3 cm. Aucune justification n’est attendue pour cette construction.
2. Démontrer que le
triangle DAH est rectangle.
Le triangle DAH est inscrit dans un demi-cercle de diamètre DH. Ce
triangle est rectaangle en A.
3. Calculer la
mesure de l’angle BEH.
Le polygone réguliier à 8 côtés est inscrit dans le cercle de centre O.
Les angles au centre formés par deux sommets consécutifs ont même
mesure, dans ce cas 360 / 8 = 45°.

Exercice 2.
Léa
a besoin de nouveaux cahiers. Pour les acheter au meilleur prix, elle
étudie les offres promotionnelles de trois magasins. Dans ces trois
magasins, le modèle de cahier dont elle a besoin a le même prix avant
promotion.
Magasin A :Cahier à l’unité ou lot de 3 cahiers pour le
prix de 2.
Magasin B:
Pour un
cahier acheté, le deuxième à moitié prix.
Magasin C
: 30% de
réduction sur chaque cahier acheté.
1. Expliquer
pourquoi le magasin C est plus intéressant si elle n’achète qu’un
cahier.
Dans les magasins A et B l'achat d'un seul cahier ne donne aucune
réduction.
Dans le magasin C l'achat d'un seul cahier donne une réduction de 30%.
2. Quel magasin
doit-elle choisir si elle veut acheter :
a. deux cahiers ?
On note x le prix d'un cahier avant promotion.
A : 2x ; B : x +0,5 x = 1,5 x. C : réduction 0,3x soit prix payé
: 2(0,7x) = 1,4 x.
C est le plus intéressant.
b. trois cahiers ?
A : 2x ; B 2x+0,5 x = 2,5 x ; C : 3(0,7x) = 2,1x.
A est le moins cher.
3. La carte de
fidélité du magasin C permet d’obtenir 10% de réduction sur le ticket
de caisse, y compris sur les articles ayant déjà bénéficié d’une
première réduction.
Léa possède cette carte de fidélité, elle l’utilise pour acheter un
cahier. Quel pourcentage de réduction totale va-t-elle obtenir ?
Prix promotion : 0,7 x ; réduction carte de fidélité : 0,07x ;
prix payé : 0,63x ; réduction 0,37 ( 37 %).
|
| .
. |
|
|
Exercice 3.
Voici un programme de calculs :
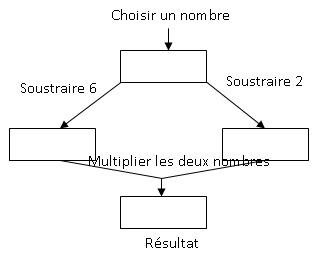
1. Montrer que si
on choisit 8 comme nombre de départ, le programme donne 12 comme
résultat.
8
8-6 =2 ; 8-2=6 ;
2 x6 = 12.
2. Pour chacune des
affirmations suivantes, indiquer si elle est vraie ou fausse.
On rappelle que les réponses doivent être justifiées.
Proposition 1
: Le programme peut donner un résultat négatif. Vrai.
Soit n le nombre positif choisi ; (n-6) (n-2) : si n appartient à
l'intervalle ]2 ; 6 [, le résultat est négatif.
Proposition 2
: Si on choisit 0,5 comme nombre de départ, le programme donne 33 /4. Vrai.
0,5-6 = -5,5 ; 0,5-2 = -1,5 ; (-5,5) x(-1,5)= = 33 /4.
4 comme résultat.
Proposition 3 : Le
programme donne 0 comme résultat pour exactement deux nombres. Vrai.
(n-6) (n-2) = 0 donne n = 2 et n = 6.
Proposition 4 : La
fonction qui, au nombre choisi au départ, associe le résultat du
programme est une fonction linéaire. Faux.
(n-6)(n-2) = n2 -8n+12 diffère de a n +b avec a et b réels.
Exercice 4.
Un
sac contient 20 jetons qui sont soit jaunes, soit verts, soit rouges,
soit bleus. On considère l’expérience suivante : tirer au hasard un
jeton, noter sa couleur et remettre le jeton dans le sac. Chaque jeton
a la même probabilité d’être tiré.
1. Le professeur,
qui connaît la composition du sac, a simulé un grand nombre de fois
l’expérience avec un tableur. Il a représenté ci-dessous la fréquence
d’apparition des différentes couleurs après 1 000 tirages.
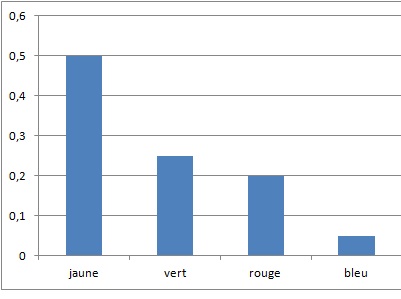
a. Quelle couleur
est la plus présente dans le sac ? Aucune justification n’est attendue.
La fréquence du jaune est la plus grande. Les jetons jaunes sont
majoritaires.
b. Le professeur a
construit la feuille de calcul suivante :
|
A
|
B
|
C
|
1
|
Nombre
de tirages
|
Nombre
de fois ou un jeton rouge apparaît
|
Fréquence
d'apparition du rouge
|
2
|
1
|
0
|
0
|
3
|
2
|
0
|
0
|
4
|
3
|
0
|
0
|
5
|
4
|
0
|
0
|
6
|
5
|
0
|
0
|
7
|
6
|
1
|
0,166
666 667
|
8
|
7
|
1
|
0,142
857 142
|
9
|
8
|
1
|
0,125
|
10
|
9
|
1
|
0,111
111 111
|
11
|
10
|
1
|
0,1
|
Quelle formule a-t-il
saisie dans la cellule C2 avant de la recopier vers le bas ?
=B2 / A2
2. On sait que la
probabilité de tirer un jeton rouge est de 0,2. Combien y a-t-il de
jetons rouges dans ce sac ?
Nombre total de jetonx x 0,2 = 20 x 0,2 = 4.
|
|
|
|
Exercice 5. QCM
1. Quand on double
le rayon d’une boule, son volume est par : 2 ; 4 ; 6 ; 8. ( 23 = 8).
2. Une vitesse
égale à 36 km.h−1 correspond à : 10 m/s ; 60 m/s ; 100 m/s ; 360 m/s.
(36 / 3,6 =10 m/s).
3. Quand on divise
racine carrée (525) par 5 on obtient :
21 racine carrée (5) ; 5 racine carrée (21) ; racine carrée (21) ; racine carrée (105).
4. On donne : 1To
(téraoctet) = 1012 octets et 1 Go (gigaoctet) = 109
octets. On partage un disque dur de 1,5 To en dossiers de 60 Go chacun.
Le nombre de dossiers obtenus est égal à : 25 ; 1000 ; 4 x 1022 ;
2,5 x 1019.
1,5 1012 / (60 x109 )= 1500 / 60 = 25.
Exercice 6.
Pour
savoir si les feux de croisement de sa voiture sont réglés
correctementcorrectement, Pauline éclaire un mur vertical comme
l’illustre le dessin :
P désigne le phare, assimilé à un point.
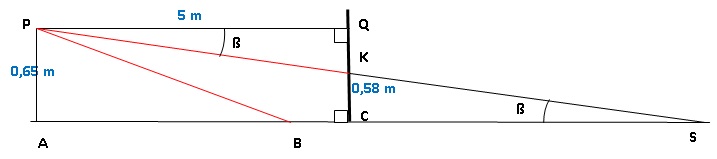
Pour que l’éclairage d’une voiture soit conforme, les constructeurs
déterminent l’inclinaison du faisceau. Cette inclinaison correspond au
rapport
QK / QP . Elle est correcte si ce rapport est compris entre 0,01 et
0,015.
1. Vérifier que les
feux de croisement de Pauline sont réglés avec une inclinaison égale à
0,014.
QK = 0,65 -0,58 = 0,07 m ; Qk / PQ = 0,07 / 5 = 0,014.
2. Donner une
mesure de l’angle �QPK correspondant à l’inclinaison. On arrondira au
dixième de degré.
tan ( angle QPK)= tan ß= QK / PQ = 0,014 ; mesure de cet angle ß= 0,80°.
3. Quelle est la
distance AS d’éclairage de ses feux ? Arrondir le résultat au mètre
près.
Dans le triangle PAS rectangle en A : tan ß = AP / AS ; AS = AP /tan ß
= 0,65 / 0,014 ~46 m.
|
|
Exercice 7.
Un
agriculteur produit des bottes de paille parallélépipédiques.
Information 1 : Dimensions des bottes de paille : 90 cm× 45 cm× 35 cm.
Information 2 : Le
prix de la paille est de 40 € par tonne.
Information 3 : 1 m3 de paille a une masse de 90 kg.
1. Justifier que
le prix d’une botte de paille est 0,51 € (arrondi au centime).
Volume d'une botte : 0,9 x 0,45 x 0,35 ~0,142 m3.
Masse = volume x masse volumique = 0,142 x 90 =12,76 kg.
Prix : 12,76 x 40 / 1000 = 0,51 €.
2. Marc veut
refaire l’isolation de la toiture d’un bâtiment avec des bottes de
paille parallélépipédiques. Le bâtiment est un prisme droit dont les
dimensions sont données sur le
schéma ci-dessous.
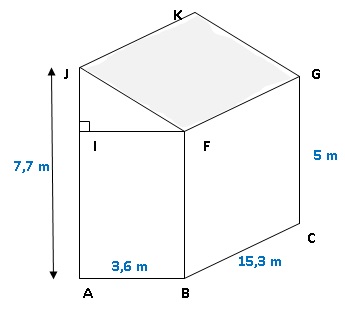
Il disposera les bottes de paille sur la surface correspondant à la
zone grisée, pour créer une isolation de 35 cm d’épaisseur.
Pour calculer le nombre de bottes de paille qu’il doit commander, il
considère que les bottes sont disposées les unes contre les autres. Il
ne tient pas compte de l’épaisseur des planches entre lesquelles il
insère les bottes.
a. Combien de
bottes devra-t-il commander ?
JF2 = IJ2 +IF2 = (7,7-5)2
+3,62 = 20,25 ; JF = 4,5 m.
Aire du toit rectangulaire : JF x FG = 4,5 x15,3 = 68,85 m2.
Aire d'une botte rectangulaire : 0,9 x0,45 = 0,405 m2.
Nombre de bottes : 68,85 / 0,405 = 170 bottes.
b. Quel est le coût
de la paille nécessaire pour isoler le toit ?
170 x0,51 = 86,7 €.
|
|