Mathématiques,
Brevet des collèges Polynésie septembre 2014
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Voici trois calculs effectués à la calculatrice.Détailler ces calculs
afin de comprendre
les résultats donnés par la calculatrice :
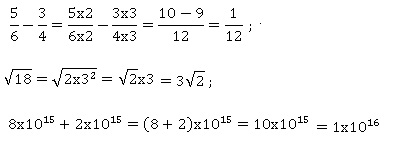
Exercice 2.
Pour choisir un écran de télévision, d’ordinateur ou une tablette
tactile, on peut s’intéresser :
• à son format qui est le rapport longueur de l’écran largeur de l’écran
• à sa diagonale qui se mesure en pouces. Un pouce est égal à 2,54 cm.
1. Un écran de
télévision a une longueur de 80 cm et une largeur de 45 cm.
S’agit-il d’un écran de format 4 / 3 ou 16 / 9 ?
80 / 45 = 16 x5 / (5x9) = 16 / 9.
2. Un écran est
vendu avec la mention « 15 pouces ». On prend les mesures suivantes :
la longueur est 30,5 cm et la largeur est 22,9 cm. La mention « 15
pouces » est-elle bien adaptée à cet écran ?
15 x2,54 = 38,1 cm.
Diagonale 2 = largeur2 + longueur 2
= 22,92 +30,52 = 1454,66 ; diagonale = 38,1 cm,
en accord avec 15 pouces.
3. Une tablette
tactile a un écran de diagonale 7 pouces et de format 4 /3. Sa longueur
étant égale à 14,3 cm, calculer sa largeur, arrondie au mm près.
Longueur / largeur = 4 / 3 ; largeur = 3 / 4 x longueur = 3 / 4 x14,3 =
10,7 cm.
|
|
|
Exercice 3.
1. Une bouteille opaque contient 20 billes dont les couleurs
peuvent être différentes.
Chaque bille a une seule couleur. En retournant la bouteille, on fait
apparaître au goulot une seule bille à la fois. La bille ne peut pas
sortir de la bouteille.
Des élèves de troisième cherchent à déterminer les couleurs des billes
contenues dans la bouteille et leur effectif. Ils retournent la
bouteille 40 fois et obtiennent le tableau suivant :
Couleur
apparue
|
rouge
|
bleue
|
verte
|
Nombre
d'apparition de la couleur
|
18
|
8
|
14
|
Ces
résultats permettent-ils d’affirmer que la bouteille contient
exactement 9 billes rouges, 4 billes bleues et 7 billes vertes ?
Non, il faudrait retourner la bouteille un nombre de fois bien
supérieur à 40.
On peut simplement affirmer que sur 40 expériences :
la probabilité du rouge est 18/40 = 9 / 20 ; celle du bleu est 8/40 = 4
/ 20 et celle du vert est 14/40 = 7 / 20.
2. Une seconde
bouteille opaque contient 24 billes qui sont soit bleues, soit rouges,
soit vertes.
On sait que la probabilité de faire apparaître une bille verte en
retournant la bouteille est égale à
3 / 8 = 0,375 et la probabilité de faire apparaitre une bille bleue est
égale à 0,5. Combien de billes rouges contient la bouteille ?
Probabilité du rouge = 1 -0,375 -0,5 = 0,125.
Nombre de billes rouges : 0,125 x 24 = 3.
Exercice 4.
La figure
ci-dessous, qui n’est pas dessinée en vraie grandeur, représente un
cercle (C) et plusieurs segments.
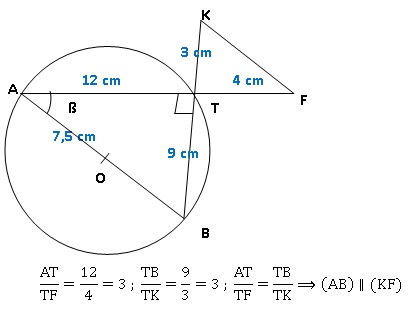
1. Démontrer
que le triangle ATB est rectangle.
Le triangle ATB est inscrit dans un demi-cercle de diamètre AB. Ce
triangle est donc rectangle en T.
2. Calculer la
mesure de l’angle ß arrondie au degré près.
tan ß =TB / AT = 9 / 12 = 0,75 ; ß = 36,9 ~37°.
3. Les droites
(AB) et (KF) sont-elles parallèles ?
4. Calculer l’aire
du triangle TKF.
Aire de ce triangle rectangle en T : TF x KF / 2 = 3 x 4 /2 =6 cm2.
|
|
|
|
Exercice 5.
Pour
son anniversaire, Julien a reçu un coffret de tir à l’arc. Il tire une
flèche. La trajectoire de la pointe de cette flèche est représentée
ci-dessous.
La courbe donne la hauteur en mètres (m) en fonction de la distance
horizontale en mètres (m) parcourue par la flèche
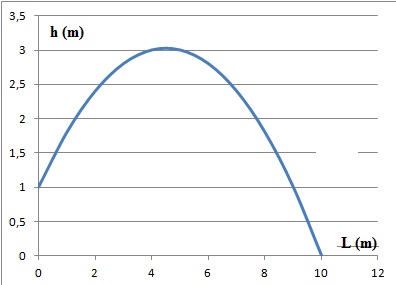
1. Dans cette
partie, les réponses seront données grâce à des lectures graphiques.
Aucune justification n’est attendue sur la copie.
a. De quelle
hauteur la flèche est-elle tirée ? 1 m
b. À quelle
distance de Julien la flèche retombe-t-elle au sol ? 10 m
c. Quelle est la
hauteur maximale atteinte par la flèche ? 3 m
2. Dans cette
partie, les réponses seront justifiées par des calculs :
La courbe ci-dessus représente la fonction f définie par f (x) = −0,1x2
+0,9x +1.
a. Calculer f (5).
f(5) =-0,1 x52 +0,9 x5 +1 = -2,5 +4,5+1 = 3 m.
b. La flèche s’
élève-t-elle à plus de 3 m de hauteur ?
Non, 5 m est la hauteur maximale aatteinte, cela correspond au maximum
de la courbe.
Exercice 6.
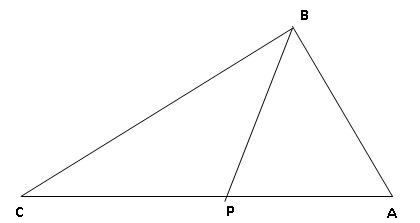
ABC est un triangle tel que AB = 5 cm, BC = 7,6 cm et AC = 9,2 cm.
1. Tracer ce
triangle en vraie grandeur.
2. ABC est-il un
triangle rectangle ?
AC2 = 9,22 = 84,64.
AB2 +BC2 =52 +7,62 =25+ =
82,76.
La relation de Pythagore n'est pas vérifiée : ce triangle n'est pas
rectangle.
3. Avec un
logiciel, on a construit ce triangle, puis :
- on a placé un point P mobile sur le côté [AC] ;
- on a tracé les triangles ABP et BPC ;
- on a affiché le périmètre de ces deux triangles.
Périmètre de ABP = 13,29 ; périmètre de BPC = 17,09
a. On déplace le
point P sur le segment [AC].
Où faut-il le placer pour que la distance BP soit la plus petite
possible ?
PB doit être perpendiculaire à AC.
b. On place
maintenant le point P à 5 cm de A.
Lequel des triangles ABP et BPC a le plus grand périmètre ?
Périmètre de ABP : AB +BP +AP = 5 +BP +5 = 10 + BP.
Périmètre de BPC : PB + PC +BC = PB +(9,2-5) +7,6 =BP + 11,8, valeur
supérieure à 10 +BP.
Le triangle BPC a le plus grand périmètre.
c. On déplace à
nouveau le point P sur le segment [AC].
Où faut-il le placer pour que les deux triangles ABP et BPC aient le
même périmètre ?
Périmètre de ABP : AB +BP +AP = 5 +BP +x = 5+x + BP.
Périmètre de BPC : PB + PC +BC = PB +(9,2-x) +7,6 =BP + 16,8 -x.
5+x + BP = BP + 16,8 -x.
5+x =16,8-x ; 2x = 16,8 -5 = 11,8 ; x = 11,8 / 2 = 5,9.
Placer P à 5,9 cm de A.
|
|
Exercice 7.
On
considère ces deux programmes de calcul :
Programme A :
Choisir un nombre
Soustraire 0,5
Multiplier le résultat par le double du nombre choisi au départ
Programme B : Choisir
un nombre
Calculer son carré
Multiplier le résultat par 2
Soustraire à ce nouveau résultat le nombre choisi au départ
1. a. Montrer que
si on applique le programme A au nombre 10, le résultat est 190.
10-0,5 = 9,5.
9,5 x2x10 =190.
b. Appliquer le
programme B au nombre 10.
102 = 100 ; 100 x2 = 200 ; 200 -10 = 190.
2. On a utilisé un
tableur pour calculer des résultats de ces deux programmes.
Voici ce qu’on a obtenu :
|
A
|
B
|
C
|
1
|
Nombre
choisi
|
Programme
A
|
Programme
B
|
2
|
1
|
1
|
1
|
3
|
2
|
6
|
6
|
4
|
3
|
15
|
15
|
5
|
4
|
28
|
28
|
6
|
5
|
45
|
45
|
7
|
6
|
66
|
66
|
a. Quelle formule
a-t-on saisie dans la cellule C2 puis recopiée vers le bas ?
=A2*A2*2-A2
b. Quelle
conjecture peut-on faire à la lecture de ce tableau ?
Les deux programmes donnent le même résultat.
c. Prouver cette
conjecture.
Soit x le nombre choisi.
Programme A : (x-0,5) 2x = 2x2 -x.
programme B : 2x2-x.
3.
Quels sont les deux nombres à choisir au départ pour obtenir 0 à
l’issue de ces programmes ?
2x2 -x = x(2x-1) =0 ;
solutions x=0 et x = 0,5.
Exercice 8.
Un couple a acheté une maison avec piscine en vue de la louer. Pour cet
achat, le couple a effectué un prêt auprès de sa banque. Ils louent la
maison de juin à septembre et lamaison reste inoccupée le reste de
l’année.
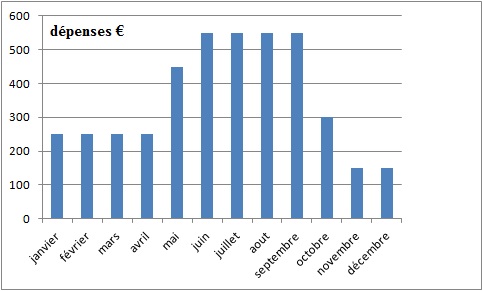
Information 1 : Dépenses liées à cette maison pour l’année 2013
Le diagramme ci-dessous présente, pour chaque mois, le total des
dépenses dues aux différentes taxes, aux abonnements (électricité,
chauffage, eau, internet), au remplissage et au chauffage de la piscine.
Remboursement mensuel du prêt.
Chaque mois, le couple doit verser 700 euros à sa banque pour
rembourser le prêt.
Information 3 : Tarif de location de lamaison.
4 semaines en juin pour 750 € la semaine.
7 semaines en juillet août pour .... € la semaine.
5 semaines en aout septembre pour 750 € la semaine.
Pour l’année 2014, avec l’augmentation des différents tarifs et taxes,
le couple prévoit que le montant des dépenses liées à lamaison sera
6%plus élevé que celui pour 2013.
Expliquer pourquoi le total des dépenses liées à la maison s’élèvera à
4 505 € en 2014.
Dépenses totale en 2013 : 250 x4 +450 +4 x550 +300 +2x150 =4250 €
4250 x1,06=4505 €.
On suppose que le couple arrive à louer sa maison durant toutes les
semaines de la période de location. À quel tarif minimal (arrondi à la
dizaine d’euros) doit-il louer sa maison entre le 5/07 et 23/08 pour
couvrir les frais engendrés par la maison sur toute l’année 2014 ?
Dépense totale : 4505 + 12 x700 = 12905 €.
Gain : 4 x750 + 7 N +5 x750 = 12905 ; 7N = 12905- 6750=6155.
N = 6155 / 7 ~880 €.
|
|